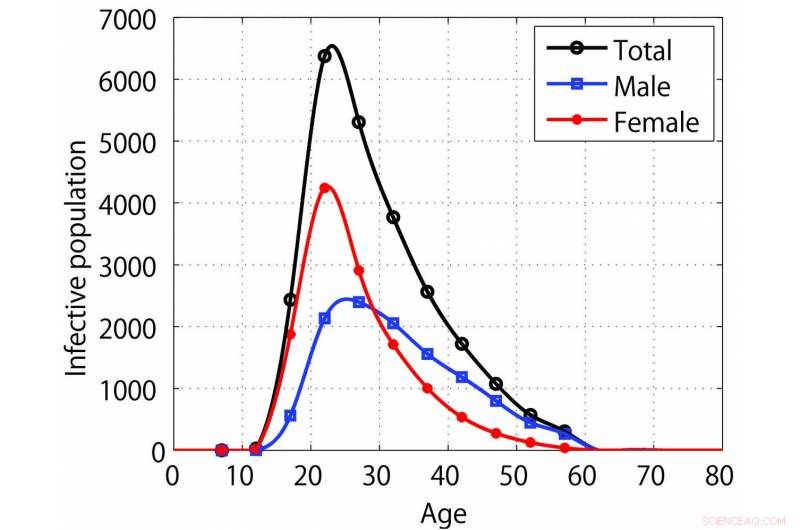
Interpolación de distribuciones por edad de casos notificados de clamidia en Japón en 2015. Crédito:Toshikazu Kuniya, Revista SIAM de Matemática Aplicada .
Los modelos matemáticos que cuantifican la dinámica de las enfermedades infecciosas son herramientas predictivas cruciales para el control de brotes en curso y futuros. El número de reproducción básico de una infección (R 0 ) es especialmente importante para el modelado de enfermedades y la epidemiología, ya que determina el comportamiento global y mide la transferibilidad de una enfermedad dentro de una población totalmente susceptible. En breve, R 0 ayuda a los funcionarios de salud pública a discernir la intensidad de una epidemia y la probabilidad de que se propague con éxito. Si R 0 > 1, ocurre un brote. Si R 0 <1, la infección normalmente desaparece.
A veces, una enfermedad es endémica, lo que significa que está continuamente presente y se mantiene en un nivel de línea de base en una ubicación específica. En estos casos, el número de individuos infecciosos permanece casi estático y en equilibrio endémico. Clamidia una enfermedad de transmisión sexual tanto en hombres como en mujeres que puede causar un daño significativo al sistema reproductivo de la mujer, ha sido endémica en Japón desde 2012. Para estimar matemáticamente R 0 por la omnipresencia de la clamidia en Japón, hay que aclarar la estabilidad del equilibrio endémico del modelo correspondiente.
En un artículo publicado el 19 de febrero en el Revista SIAM de Matemática Aplicada , una publicación de la Sociedad de Matemáticas Industriales y Aplicadas, Toshikazu Kuniya estudia el comportamiento global de un modelo epidémico SIR multigrupo con estructura de edad y utiliza el modelo para estimar R 0 para el brote de clamidia en Japón. Kuniya ha estado modelando enfermedades infecciosas desde que era estudiante de maestría y siente especial curiosidad por su comportamiento global. "Recientemente me he interesado en la aplicación de modelos epidémicos a sus consideraciones epidemiológicas, ", dijo." Creo que el comportamiento global de los modelos epidémicos juega un papel importante en la comprensión de los datos de enfermedades infecciosas a largo plazo ".
Un modelo SIR, que significa susceptible, infeccioso, y recuperado — es un modelo compartimental simple y uno de los mecanismos más básicos de la epidemiología matemática. Divide la población total de un área afectada en las tres clases antes mencionadas. Este tipo de modelo converge a un equilibrio libre de enfermedad cuando R 0 <1 y un equilibrio endémico cuando R 0 > 1.
Si bien el modelo de Kuniya es bastante similar al empleado por investigadores anteriores, Kuniya lo reformatea en un modelo multigrupo con susceptibilidad dependiente de la edad. "Elegí un modelo epidémico SIR multigrupo con estructura de edad porque es útil para manejar los datos con la heterogeneidad (sexo, la edad, posición, etc.) de cada persona, ", dijo." La estructura de edad nos permite considerar los efectos de la variación en el tiempo de la distribución demográfica por edades y la dependencia de la edad de cada parámetro de la epidemia ".
Por el bien de la simplicidad, Kuniya asume que la suma de las tasas de mortalidad y recuperación es constante. También debilita algunas de las suposiciones restrictivas del modelo anterior que impedían una aplicación exitosa. "Según el supuesto anterior, el coeficiente de transmisión de la enfermedad fue independiente del estado de los individuos infecciosos, "Dijo Kuniya." En este estudio, hemos debilitado este supuesto para poder considerar la posible dependencia del coeficiente de transmisión de la enfermedad del estado de los individuos infecciosos. En virtud de esto, podemos modelar la transmisión de la enfermedad de individuos masculinos a individuos femeninos y viceversa ". Hacerlo le permite demostrar que R 0 determina completamente el comportamiento global del modelo. También elimina la posibilidad de un equilibrio endémico inestable si R 0 > 1.
Después de establecer su modelo, Kuniya lo aplica a la manifestación de clamidia de 2015 en Japón, para lo cual existe un conjunto de datos heterogéneos disponibles ordenados por edad y sexo. El estado aparentemente endémico de la clamidia en los últimos años también convirtió a la enfermedad en un objetivo apropiado. Kuniya examina cuatro casos particulares:en forma de modelo homogéneo, un modelo de dos sexos independiente de la edad, un modelo de un sexo dependiente de la edad, y un modelo de dos sexos dependiente de la edad, y compara los resultados estimados de R 0 . Estos casos especiales producen una R 0 estiman entre 1.0148 y 1.0535 para clamidia en Japón. Su análisis también revela que la introducción de una estructura por edades impacta el valor de R 0 con más fuerza que la aplicación de una estructura de dos grupos. Esto indica que los modelos de ecuaciones diferenciales ordinarias que carecen de estructura por edades, aunque suelen ser más fáciles de usar que los modelos de ecuaciones diferenciales parciales con estructura por edades, podrían, en última instancia, subestimar R 0 .
A lo largo del curso de su investigación, Kuniya asume que todos los individuos infecciosos están documentados, cuando en realidad algunos casos de clamidia probablemente no se notifiquen, especialmente porque la enfermedad a menudo no muestra síntomas. Esta discrepancia puede haber llevado a subestimar R 0 valores para los cuatro casos individuales. Tener en cuenta los casos no notificados y mejorar la precisión general de la estimación es una tarea para el próximo estudio.
En el futuro, Kuniya espera aplicar sus hallazgos a modelos más generales con más de dos grupos, lo que requiere un conjunto de datos cada vez más elaborado. "Creo que podemos mejorar la estimación de R 0 y otros parámetros epidémicos mediante el uso de un conjunto de datos más detallado subdividido según la heterogeneidad, por ejemplo, actividad sexual — de cada individuo, ", dijo." Podemos aplicar nuestros resultados teóricos a casos más generales con números arbitrarios de grupos ".