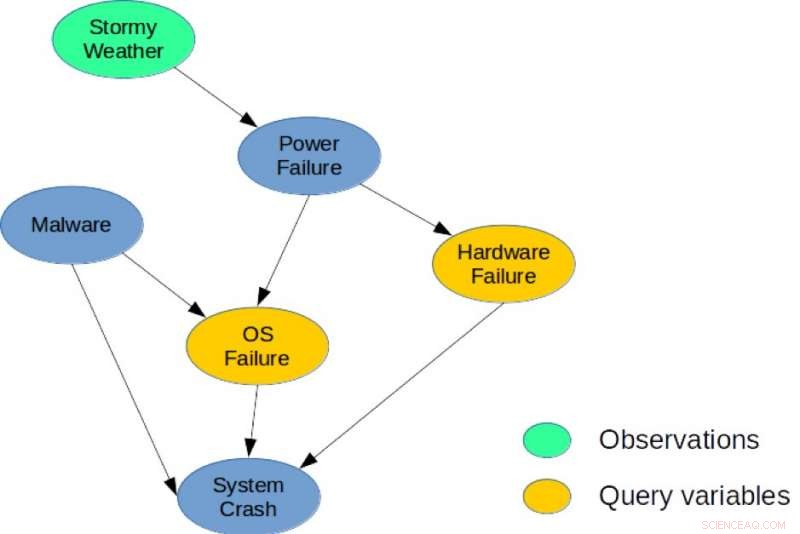
Figura 1. Una red bayesiana simple para una tarea de diagnóstico del sistema. Crédito:IBM
Existe una profunda conexión entre la planificación y la inferencia, y durante la última década, Múltiples investigadores han introducido reducciones explícitas que muestran cómo la planificación estocástica se puede resolver usando inferencia probabilística con aplicaciones en robótica. Planificación, y problemas ambientales. Sin embargo, Los métodos heurísticos y la búsqueda siguen siendo los enfoques de mejor rendimiento para la planificación en grandes espacios combinatorios de estado y acción. Mis coautores y yo adoptamos un nuevo enfoque en nuestro artículo, "De la planificación estocástica al MAP marginal" (autores:Hao Cui, Radu Marinescu, Roni Khardon), en la Conferencia de 2018 sobre Sistemas de Procesamiento de Información Neural (NeurIPS) mostrando cómo las ideas de la planificación se pueden utilizar para la inferencia.
Desarrollamos el solucionador algebraico basado en gradientes (AGS), un solucionador novedoso para la inferencia MAP marginal aproximada. El algoritmo construye un gráfico de cálculo algebraico aproximado que captura los márgenes de las variables de estado y recompensa bajo supuestos de independencia. Luego utiliza la diferenciación automática y la búsqueda basada en gradientes para optimizar la elección de acciones. Nuestro análisis muestra que el valor calculado por el gráfico de cálculo AGS es idéntico a la solución de la propagación de creencias (BP) cuando está condicionado a las acciones. Esto proporciona una conexión explícita entre los algoritmos de planificación heurística y la inferencia aproximada.
Más específicamente, revisamos la conexión entre la planificación estocástica y la inferencia probabilística. Proponemos por primera vez utilizar un algoritmo heurístico eficiente que fue diseñado originalmente para resolver problemas de planificación para abordar una tarea de inferencia central para modelos gráficos probabilísticos, a saber, la tarea de probabilidad marginal máxima a posteriori (MMAP).
Los modelos gráficos probabilísticos, como las redes bayesianas o las redes de Markov, proporcionan un marco muy poderoso para razonar sobre estructuras de dependencia condicional sobre muchas variables. Para tales modelos, la consulta de inferencia MMAP es una tarea particularmente difícil pero importante, correspondiente a encontrar la configuración más probable (o maximizar la probabilidad) sobre un subconjunto de variables, llamadas variables MAP, después de marginar (o resumir) el resto del modelo.
La inferencia de MMAP surge en muchas situaciones, especialmente en tareas de diagnóstico y planificación, en el que la especificación más natural del modelo contiene muchas variables cuyos valores no nos importa predecir, pero que crean interdependencia entre las variables de interés. Por ejemplo, en una tarea de diagnóstico basada en modelos, dadas las observaciones, buscamos optimizar un subconjunto de variables de diagnóstico que representan componentes potencialmente defectuosos en un sistema.
Por ilustracion, considere la red bayesiana que se muestra en la Figura 1, que describe un problema de diagnóstico simple para un sistema informático. El modelo captura las dependencias causales directas entre seis variables aleatorias utilizadas para describir este problema. Específicamente, un bloqueo del sistema puede deberse a una falla de hardware, una falla del sistema operativo, o la presencia de Malware en el sistema. Similar, una falla de energía podría ser una causa común de falla de hardware y sistema operativo, y el clima tormentoso pueden causar un corte de energía. Una posible consulta de MMAP sería calcular la configuración más probable de fallas de hardware y sistema operativo, dado que observamos Stormy Weather, independientemente del estado de las otras variables (Malware, Fallo del sistema, o falla de energía).
Los marcos de planificación estocásticos, como los procesos de decisión de Markov, se utilizan ampliamente para modelar y resolver tareas de planificación en condiciones de incertidumbre. La planificación de horizonte finito se puede capturar utilizando una red bayesiana dinámica (DBN) donde las variables de estado y acción en cada paso de tiempo se representan explícitamente y las distribuciones de probabilidad condicional de las variables están dadas por las probabilidades de transición. En la planificación fuera de línea, la tarea consiste en calcular una política que optimice la recompensa a largo plazo. A diferencia de, en la planificación en línea se nos da un tiempo limitado fijo t por paso y no podemos calcular una política por adelantado. En lugar de, dado el estado actual, el algoritmo debe decidir la siguiente acción dentro del tiempo t. Entonces se realiza la acción, se observan una transición y una recompensa y el algoritmo se presenta con el siguiente estado. Este proceso se repite y se evalúa el rendimiento a largo plazo del algoritmo.
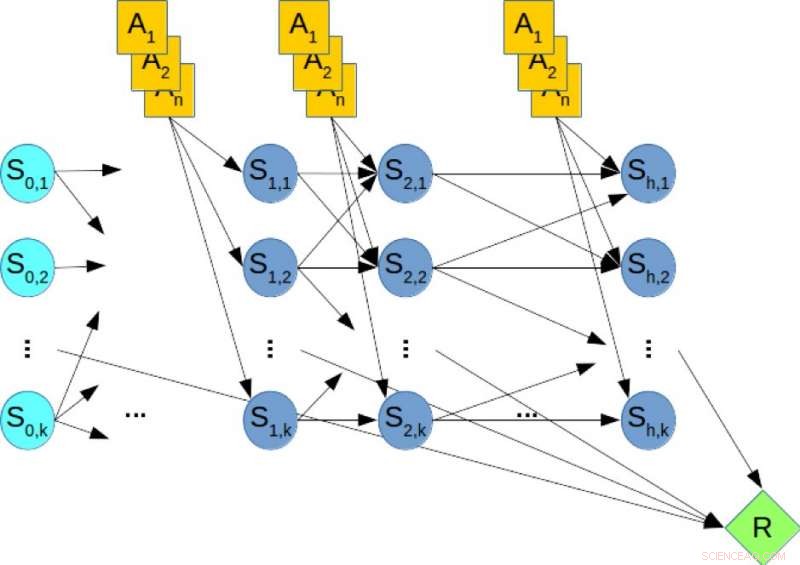
Figura 2. Una red bayesiana dinámica (DBN) para planificación estocástica. Crédito:IBM
Por ilustracion, considere la Figura 2, que muestra el DBN correspondiente a un problema de planificación hipotético, donde los nodos naranjas representan las variables de acción, los nodos azules denotan las variables de estado, y el nodo verde denota la recompensa acumulativa que debe maximizarse. Por lo tanto, calcular la política óptima del problema de planificación es equivalente a resolver una consulta MMAP sobre el DBN, donde maximizamos las variables de acción y marginamos las variables de estado.
Nuestra evaluación experimental de casos de problemas de MMAP difíciles muestra de manera concluyente que el esquema AGS mejora el rendimiento en cualquier momento de los algoritmos de última generación en problemas de MMAP con subproblemas de suma dura. a veces hasta en un orden de magnitud. Creemos que estas conexiones entre planificación e inferencia se pueden explorar más a fondo para producir mejoras en ambos campos.
Esta historia se vuelve a publicar por cortesía de IBM Research. Lea la historia original aquí.