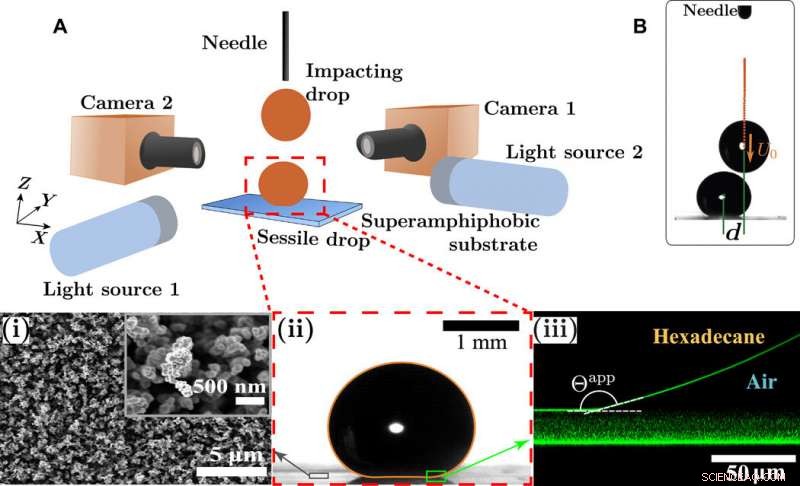
Enfoque experimental y la gota sésil. (A) Esquema de la configuración experimental para el impacto de la gota binaria en superficies superampifóbicas. La aguja está fija para establecer la altura de impacto en la dirección Z y la distancia relativa entre las gotas sésiles y las que impactan. La gota sésil se centra primero a lo largo del plano YZ. Luego, la gota impactante se dispensa desde la aguja mientras que el impacto se monitoriza con la cámara 2. La cámara 1 se usa para determinar las posiciones relativas de las gotas en la dirección X. Las cámaras y las fuentes de luz están alineadas para observar el impacto tanto en los planos XZ como YZ. Recuadros:(i) Imagen SEM de una superficie con plantilla de hollín a dos aumentos. (ii) Gota de hexadecano (V ≈ 3 μl) descansando sobre la superficie superampifóbica. El contorno naranja es la solución de la ecuación. 1 para un número de enlace correspondiente Bo =0.3. (iii) Imagen confocal que muestra una gota de hexadecano en la superficie superampifóbica. La imagen ilustra el ángulo de contacto aparente de la gota con la superficie (Θapp ≈ 164 °). La imagen se toma en modo de reflexión, es decir., no se añadió colorante al hexadecano. La reflexión de la luz resulta de las diferencias entre los índices de refracción del hexadecano (1.43), aire (1.0), y vidrio y sílice (~ 1,46). La capa superampifóbica se compone principalmente de aire, y por lo tanto, su índice de refracción es cercano a 1. Por lo tanto, son visibles la capa de vidrio horizontal superampifóbica y las interfaces de la capa de hexadecano superampifóbica. La capa superampifóbica en sí es visible como un patrón difuso, resultante del reflejo de la luz de las nanopartículas de sílice. (B) Imagen que muestra una colisión descentrada. El parámetro de impacto es χ =d / (2R). Crédito de la foto:Olinka Ramírez-Soto, Instituto Max Planck de Investigación de Polímeros. Crédito:Science Advances, doi:10.1126 / sciadv.aba4330
Las gotas que chocan son omnipresentes en las tecnologías cotidianas, como los motores de combustión y los aerosoles, y en procesos naturales como las gotas de lluvia y la formación de nubes. Los resultados de la colisión dependen de la velocidad del impacto, grado de alineación, propiedades intrínsecas de tensión superficial y una superficie de baja humectación. En un nuevo informe sobre Avances de la ciencia , Olinka Ramírez-Soto y un equipo de científicos en investigación de polímeros, dinámica de fluidos, ingeniería química y de materiales en Alemania, Holanda y Estados Unidos investigaron la dinámica de una gota de aceite que impacta una gota sésil idéntica en una superficie superampifóbica. Una superficie superampifóbica es análoga a la superhidrofobicidad (repelencia al agua), aunque puede repeler líquidos polares y apolares. Usando simulaciones numéricas, el equipo recreó escenarios de rebote para cuantificar los perfiles de velocidad, transferencia de energía y disipación viscosa en la configuración experimental. Este trabajo mostró la influencia de la velocidad del impacto en la dinámica de rebote de las colisiones de aceite gota a gota en superficies superampifóbicas.
Investigando el impacto de gota sobre gota
Cuando una gota de líquido impacta en una gota sésil de un líquido idéntico, la expectativa intuitiva es que ambas gotas se fusionen o combinen. Este proceso es común con la lluvia y las gotas de un grifo que gotea, pero a veces, una fina capa de aire entre dos gotas puede permitir que las gotas de agua reboten perfectamente en superficies hidrófilas (amantes del agua). En el siglo XIX, El científico e ingeniero Osborn Reynolds primero registró y atribuyó el movimiento de deslizamiento de las gotas de agua a través de una piscina a este fenómeno. Una capa de vapor es igualmente responsable del efecto Leidenfrost, donde una gota se cierne sobre una superficie sobrecalentada.
A pesar de la caracterización experimental de la dinámica del impacto, faltan métodos para modelar cuantitativamente los campos de velocidad y la transferencia de energía. Los estudios sobre el impacto de gota sobre gota en superficies superampifóbicas se ven obstaculizados actualmente por un número limitado de técnicas para diseñar superficies que no se mojen. Por lo tanto, es importante comprender qué escenarios determinan el impacto del petróleo gota a gota en una superficie superampifóbica y cómo se transfiere la energía entre las gotas. En este estudio, Ramírez-Soto et al. estudiaron experimental y numéricamente la dinámica de una gota de aceite de baja tensión superficial que impacta sobre un líquido sésil de composición similar que descansa sobre una superficie superampifóbica. El equipo mostró cómo la gota de aceite impactante podía levantar la gota en reposo de la superficie sin fusionarse.
Instantáneas de la dinámica del impacto. Tenga en cuenta que las etiquetas de gota 1 y 2 son para la gota impactante y sésil, respectivamente. Se observan seis resultados (casos I a VI) al variar el parámetro de impacto χ y el número de Weber (We). Las filas corresponden a diferentes parámetros de impacto de I a IV. Las columnas muestran etapas características del proceso de colisión. A, justo en la colisión; B, caída sésil a máxima compresión; C, forma de gota justo antes de la separación o coalescencia; D, resultado final del impacto. La altura del centro de masa del impacto, sésil, o gotas unidas es máxima. El volumen de ambas gotas es de 3 μl. Caso I:We =1.30 y χ =0.01, las marcas de tiempo para cada cuadro son tA =0 ms, tB =8 ms, tC =20 ms, y tD =25 ms. Caso II:We =1,53, χ =0,08; tA =0 ms, tB =8 ms, tC =20 ms, y tD =24 ms. Caso III:We =1,44, χ =0,24; tA =0 ms, tB =8 ms, tC =20 ms, y tD =24 ms. Caso IV:We =1,48, χ =0,52; tA =0 ms, tB =5,5 ms, tC =7 ms, y tD =21 ms. Caso V:We =5.84, χ =0,08; tA =0 ms, tB =3,75 ms, tC =8,5 ms, y tD =25,5 ms. Caso VI:We =1,43, χ =0,03; tA =0 ms, tB =7,5 ms, tC =9 ms, y tD =17 ms. Crédito de la foto:Olinka Ramírez-Soto, Instituto Max Planck de Investigación de Polímeros. Crédito:Science Advances, doi:10.1126 / sciadv.aba4330 
Los científicos realizaron cuatro experimentos de rebote sin coalescencia. En el primer escenario, ambas gotas rebotan; en otros dos escenarios, la gota impactante rebota mientras la gota sésil permanece, y en el escenario final, la caída sésil rebota mientras que la caída impactante permanece en la superficie. Durante los experimentos, Ramírez-Soto et al. colocó suavemente una gota de aceite sésil en una superficie superampifóbica y la impactó con una segunda gota idéntica. Crearon la superficie superampifóbica usando una capa de 20 µm de espesor de hollín de vela con plantilla, que contenía una red porosa de nanoperlas de carbono. Para aumentar la estabilidad de la frágil red, depositaron una capa de sílice sobre las nanoestructuras porosas. Redujeron la energía superficial de la superficie con plantilla de hollín mediante la fluoración para producir una superficie superampifóbica que repele el agua y la mayoría de los aceites. Los científicos utilizaron hexadecano como aceite modelo durante los experimentos debido a una gran cantidad de propiedades favorables, incluido el comportamiento newtoniano, y registraron el ángulo de una gota de hexadecano mediante microscopía confocal. El estudio comparó cuantitativamente los datos experimentales y numéricos de la dinámica de rebote. Ramírez-Soto et al. calculó y confirmó el valor de la forma de la gota utilizando la ecuación de Young-Laplace.

Video experimental del caso I para gotas de hexadecano:rebote de gota impactante. (Número de Weber -
Resultados experimentales y simulaciones numéricas.
El equipo observó seis resultados para la dinámica del impacto. Durante el impacto, ambas gotas se deformaron y se extendieron radialmente para mostrar compresión axial, mientras que la energía cinética del sistema se transfiere a las energías superficiales de ambos. Cuando las gotas empezaron a retirarse, la gota previamente sésil transfirió energía de regreso a la gota impactante en forma de energía cinética. Después de la colisión la gota impactante rebotó, mientras que la gota sésil se quedó en el sustrato. Los científicos mantuvieron un número de Weber constante ( Nosotros ~ 1,5) para los seis casos observados; donde el parámetro caracterizó típicamente la calidad de atomización de una pulverización o el tamaño de gota resultante de las emulsiones. Luego trazaron la alineación frontal (indicada X) y aumentaron el número de Weber para la coalescencia de gotas en la configuración experimental. Atribuyeron el resultado a la inestabilidad de la capa de aire entre las gotas como resultado del contacto directo en las condiciones experimentales.
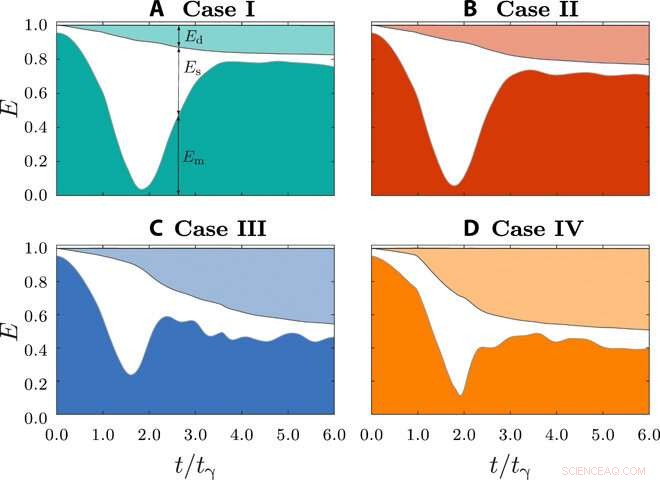
Presupuesto energético. La variación temporal de la transferencia de energía aclara las diferentes etapas del proceso de impacto gota sobre gota en We ~ 1. Inicialmente, toda la energía se almacena como energía mecánica de la gota impactante y energía superficial de la gota sésil. Luego, la energía mecánica del sistema disminuye y se transfiere a la energía superficial de las gotas. A esta transferencia le sigue una etapa de recuperación en la que la energía superficial se transfiere de nuevo a la energía mecánica del sistema. Una parte de la energía se pierde como disipación viscosa. Esta disipación viscosa considera la energía combinada disipada tanto en las gotas de líquido como en el aire circundante. Este cálculo incluye las capas de aire entre las gotas y entre las gotas y el sustrato superampifóbico. Durante el impacto, las gotas (A) caso I:χ =0, (B) caso II:χ =0.08, (C) caso III:χ =0,25, y (D) caso IV:χ =0,625. Em es la energía mecánica total del sistema (Em =Ek + Ep), Es es la energía superficial de las dos gotas, y Ed es la disipación viscosa en el sistema. Tenga en cuenta que la energía mecánica total (Em) incluye la energía del centro de masa de las gotas, así como las energías de oscilación y rotación obtenidas en el marco de referencia que se traslada con el centro de masa de las gotas individuales. Crédito:Science Advances, doi:10.1126 / sciadv.aba4330
Ramírez-Soto et al. luego realizó simulaciones numéricas directas (DNS) para ilustrar el efecto de los campos de velocidad y la transferencia de energía entre gotas y comparó los resultados con los datos experimentales. El equipo utilizó el método de volumen geométrico de fluido (VOF) y conservó una capa finita de aire entre las gotas durante todo el proceso para imitar las condiciones experimentales para lograr gotas no coalescentes mediante simulaciones. El equipo ejecutó las primeras cuatro simulaciones y cuantificó los campos del vector de velocidad para cada caso; Los resultados permitirán explorar cuantitativamente la dinámica del proceso de colisión gota a gota de petróleo.
Presupuesto energético
En todos los casos, la gota impactante contenía energía como energía mecánica (en forma de energía cinética y potencial) y como energía superficial de la gota sésil. Luego, la energía mecánica del sistema disminuyó y se transfirió a la energía superficial de las gotas combinadas. Un paso de recuperación siguió a la transferencia, en el que la energía superficial se transfiere de nuevo a la energía mecánica del sistema, mientras que una parte de la energía se disipó en forma de disipación viscosa. Este proceso representó la energía combinada disipada en las gotas de líquido y en el aire circundante. Los cálculos también tomaron en cuenta la capa de aire entre el contacto gota a gota, así como entre el sustrato gota sobre gota superampifóbico. Las simulaciones numéricas proporcionaron una descripción cuantitativa de la dinámica del impacto, donde existía un fuerte acuerdo entre los límites de las gotas y las energías mecánicas experimentales.

Experimental video of Case V (five) for hexadecane drops:coalescence of drops and lift-off of coalesced drop. Crédito:Science Advances, doi:10.1126/sciadv.aba4330
De este modo, Olinka Ramírez-Soto and colleagues combined systematic experiments and numerical simulations to predict and control the outcome of binary oil drop impacts on low-adhesion surfaces. The experimental and numeric one-on-one comparisons revealed the drop boundaries and center of mass mechanical energies, while illustrating the power of direct numerical simulations. The study highlighted how the alignment of droplet impact alone could be used to determine the recovered energy distribution between two drops after impact.
© 2020 Science X Network