Si alguna vez ha intentado desenredar un par de auriculares, comprenderá cómo los lazos y los cables pueden retorcerse. El ADN puede enredarse de la misma manera, y en algunos casos, tiene que cortarse y reconectarse para resolver los nudos. Ahora un equipo de matemáticos, biólogos e informáticos han descubierto cómo la bacteria E. coli puede desvincular el ADN enredado mediante un proceso de reconexión local. Las matemáticas detrás de la investigación, publicado recientemente en Informes científicos , podría tener implicaciones mucho más allá de la biología.

La bacteria E. coli puede causar enfermedades intestinales, pero también son caballos de batalla de laboratorio. El genoma de E. coli es un solo círculo de ADN de doble hebra. Antes de que una célula de E. coli se divida, ese círculo está copiado. Abrir la doble hélice para copiarla arroja tensiones de torsión en otras partes de la molécula, al igual que desenrollar una cuerda en un lugar hará que se enrolle en otra parte. El proceso da como resultado dos bucles de ADN retorcidos que se atraviesan como un truco de "anillos mágicos".

Para separar los anillos, E. coli usa una enzima llamada topoisomerasa IV, que corta con precisión un segmento de ADN, permite que los bucles pasen a través de la rotura y luego vuelve a sellar la rotura. Debido a que la topoisomerasa IV es tan importante para las bacterias, es un objetivo tentador para antibióticos como la ciprofloxacina. Pero cuando la topoisomerasa IV está ausente, otro complejo enzimático puede intervenir para llevar a cabo esta desvinculación, aunque de forma menos eficiente. Este complejo introduce dos rupturas y se desvincula al volver a conectar los cuatro cabos sueltos.

"Hay otras formas de desvincular los anillos, pero ¿cómo lo hacen? ”dijo Mariel Vázquez, profesor de matemáticas y de microbiología y genética molecular en la Universidad de California, Davis.

Un camino Vázquez dijo, es que las enzimas de reconexión eliminan un enlace a la vez hasta que llegan a cero. Esa solución fue favorecida por los biólogos.

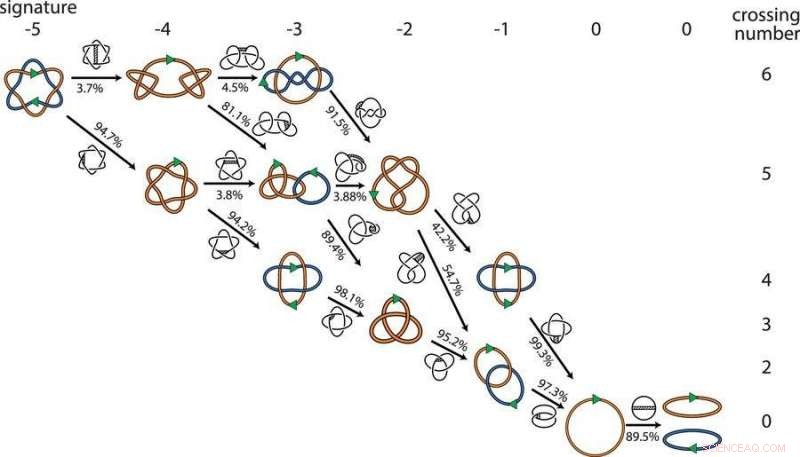
Pero los matemáticos ven el problema de manera ligeramente diferente. Entienden el ADN como una curva flexible en un espacio tridimensional. Ciertos puntos de la curva se pueden romper y volver a conectar. Para un matemático, Hay muchas rutas potenciales para que funcionen los procesos de reconexión, incluidas algunas en las que el número de enlaces aumenta antes de volver a descender.

"Son todos iguales para un matemático, pero no a un biólogo, ", Dijo Vázquez. Para determinar la ruta más probable y resolver el problema, recurrieron al modelado computacional.

Vázquez y sus colegas desarrollaron un software de computadora con ADN representado como cadenas flexibles para modelar las posibles ubicaciones donde las enzimas de reconexión podrían cortar y reconectar las cadenas. En general, modelaron millones de configuraciones que representan 881 topologías diferentes, o formas matemáticas, e identificó cientos de vías mínimas para conectar dos círculos de ADN en hasta nueve lugares hasta dos círculos separados.

El modelo informático confirmó la corazonada de los biólogos:deshacer un enlace a la vez es la ruta preferida para separar los círculos de ADN.

Los resultados podrían tener implicaciones mucho más allá de la biología del ADN, Dijo Vázquez. Hay otros ejemplos en la naturaleza de objetos que chocan, romperse y reconectarse, como la dinámica de los vórtices de fluidos vinculados, o los patrones formados por anillos de humo, por ejemplo. Cuando las erupciones solares son expulsadas del sol, poderosas líneas de campo magnético se cruzan y se vuelven a conectar.

"Las matemáticas no son específicas del ADN, y el cálculo se puede adaptar, "Dijo Vázquez.