
Investigadores de la Universidad de Rice y del Laboratorio Nacional de Oak Ridge determinaron que los materiales bidimensionales que crecen en un cono permiten controlar dónde aparecen los defectos llamados límites de grano. Estos defectos se pueden utilizar para mejorar la electrónica de los materiales, mecánico, propiedades catalíticas y ópticas. Crédito:Grupo de Investigación Yakobson / Universidad Rice
Los investigadores de la Universidad de Rice han aprendido a manipular materiales bidimensionales para diseñar defectos que mejoren las propiedades de los materiales.
El laboratorio Rice del físico teórico Boris Yakobson y sus colegas del Laboratorio Nacional Oak Ridge están combinando teoría y experimentación para demostrar que es posible dar defectos específicos a materiales 2-D, especialmente las vetas a escala atómica llamadas fronteras de grano. Estos límites se pueden utilizar para mejorar la electrónica, magnético, mecánico, propiedades catalíticas y ópticas.
La clave es introducir una curvatura en el paisaje que limite la forma en que se propagan los defectos. Los investigadores llaman a esto "topología de límite de grano de inclinación, "y lo logran haciendo crecer sus materiales sobre un sustrato topográficamente curvado, en este caso, un cono. El ángulo del cono dicta si, de qué tipo y dónde aparecen los límites.
La investigación es el tema de un artículo en la revista American Chemical Society ACS Nano .
Los límites de grano son los bordes que aparecen en un material donde los bordes se encuentran en un desajuste. Estos límites son una serie de defectos; por ejemplo, cuando dos hojas de grafeno hexagonal se encuentran en un ángulo, los átomos de carbono lo compensan formando anillos no hexagonales (de cinco o siete miembros).

Un modelo teórico a la izquierda, creado en Rice University, muestra una escama triangular de disulfuro de tungsteno que crece alrededor de un cono que fuerza la creación de un límite de grano en un ángulo específico. Los investigadores de Rice demostraron que el ancho del cono podría usarse para determinar la ubicación del límite, y los científicos del Laboratorio Nacional de Oak Ridge lo demostraron cuando hicieron el material coincidente que se ve en la imagen del microscopio electrónico de la derecha. Crédito:Universidad Rice / Laboratorio Nacional Oak Ridge
Yakobson y su equipo ya han demostrado que estos límites pueden ser significativos desde el punto de vista electrónico. Ellos pueden, por ejemplo, convertir el grafeno perfectamente conductor en un semiconductor. En algunos casos, el límite en sí mismo puede ser un cable conductor a subnanoescala o adquirir propiedades magnéticas.
Pero hasta ahora los investigadores tenían poco control sobre dónde aparecerían esos límites al cultivar grafeno, disulfuro de molibdeno u otros materiales 2-D por deposición química de vapor.
La teoría desarrollada en Rice mostró que el crecimiento de material 2-D en un cono obligaría a que los límites aparecieran en ciertos lugares. El ancho del cono controlaba la colocación y, más importante, el ángulo de inclinación, un parámetro crucial para ajustar las propiedades electrónicas y magnéticas de los materiales, Dijo Yakobson.
Los colaboradores experimentales de Oak Ridge dirigidos por el coautor David Geohegan proporcionaron evidencia que respalda aspectos clave de la teoría. Lo lograron cultivando disulfuro de tungsteno en pequeños conos similares a los de los modelos informáticos de Rice. Los límites que aparecieron en los materiales reales coincidieron con los predichos por la teoría.
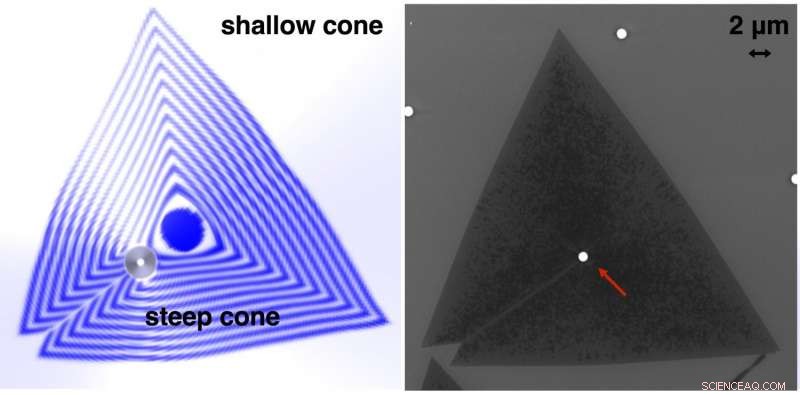
Investigadores de la Universidad de Rice y del Laboratorio Nacional de Oak Ridge predicen y confirmaron que los materiales bidimensionales que crecen en un cono permiten controlar dónde aparecen los defectos llamados límites de grano. A la izquierda un modelo de Rice predice cómo se formaría un límite de grano en un cono empinado y se extendería hacia un cono poco profundo. Los científicos de Oak Ridge confirmaron la predicción cuando crearon el material que se ve en una imagen de microscopio electrónico a la derecha. Crédito:Universidad Rice / Laboratorio Nacional Oak Ridge
"La forma no plana del sustrato obliga al cristal 2-D a crecer en un espacio curvo 'no euclidiano', "Dijo Yakobson." Esto tensa el cristal, que de vez en cuando cede dando paso a las costuras, o límites de grano. No es diferente de la forma en que un sastre agregaría una costura a un traje o un vestido para adaptarse a un cliente con curvas ".
Los conos de modelado de diferentes anchos también revelaron un "cono mágico" de 38,9 grados sobre el cual el crecimiento de un material 2-D no dejaría ningún límite de grano.
El equipo de Rice amplió su teoría para ver qué pasaría si los conos se sentaran en un avión. Ellos predijeron cómo se formarían los límites de grano en toda la superficie, y otra vez, Los experimentos de Oak Ridge confirmaron sus resultados.
Yakobson dijo que los equipos de Rice y Oak Ridge estaban trabajando en aspectos de la investigación de forma independiente. "Fue lento hasta que nos conocimos en una conferencia en Florida hace un par de años y nos dimos cuenta de que deberíamos continuar juntos, ", dijo." Sin duda fue gratificante ver cómo los experimentos confirmaron los modelos, aunque a veces ofrece importantes sorpresas. Ahora tenemos que hacer el trabajo adicional para comprenderlos también ".