Muchos de los dispositivos cuánticos actuales se basan en conjuntos de qubits, también llamados espines. Estos bits cuánticos tienen sólo dos niveles de energía, el "0" y el "1". Sin embargo, los giros en dispositivos reales también interactúan con la luz y las vibraciones conocidas como bosones, lo que complica enormemente los cálculos.
En una nueva publicación en Physical Review Letters , investigadores de Ámsterdam demuestran una forma de describir sistemas de espín-bosones y utilizarlos para configurar de manera eficiente dispositivos cuánticos en un estado deseado.
Los dispositivos cuánticos utilizan el peculiar comportamiento de las partículas cuánticas para realizar tareas que van más allá de lo que pueden hacer las máquinas "clásicas", incluida la computación cuántica, la simulación, la detección, la comunicación y la metrología. Estos dispositivos pueden adoptar muchas formas, como un conjunto de circuitos superconductores o una red de átomos o iones mantenidos en su lugar mediante láseres o campos eléctricos.
Independientemente de su realización física, los dispositivos cuánticos suelen describirse en términos simplificados como una colección de bits o espines cuánticos de dos niveles que interactúan. Sin embargo, estos espines también interactúan con otras cosas de su entorno, como la luz en los circuitos superconductores o las oscilaciones en la red de átomos o iones. Las partículas de luz (fotones) y los modos de vibración de una red (fonones) son ejemplos de bosones.
A diferencia de los espines, que sólo tienen dos niveles de energía posibles ("0" o "1"), el número de niveles para cada bosón es infinito. En consecuencia, existen muy pocas herramientas computacionales para describir espines acoplados a bosones.
En su nuevo trabajo, los físicos Liam Bond, Arghavan Safavi-Naini y Jiří Minář de la Universidad de Amsterdam, QuSoft y Centrum Wiskunde &Informatica solucionan esta limitación describiendo sistemas compuestos de espines y bosones utilizando los llamados estados no gaussianos. Cada estado no gaussiano es una combinación (una superposición) de estados gaussianos mucho más simples.
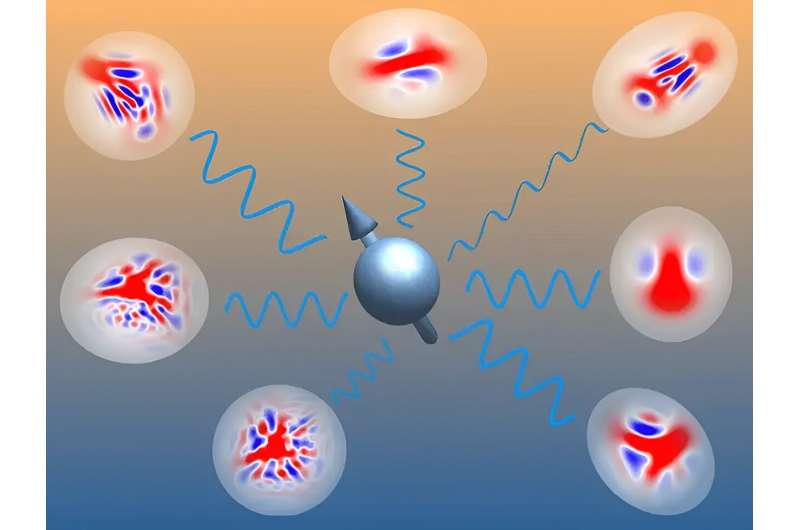
Cada patrón azul-rojo en la imagen de arriba representa un posible estado cuántico del sistema espín-bosón. "Un estado gaussiano se vería como un simple círculo rojo, sin ningún patrón azul-rojo interesante", explica Ph.D. candidato Liam Bond. Un ejemplo de estado gaussiano es la luz láser, en la que todas las ondas de luz están perfectamente sincronizadas.
"Si tomamos muchos de estos estados gaussianos y comenzamos a superponerlos (de modo que estén en una superposición), emergen estos patrones maravillosamente intrincados. Estábamos particularmente entusiasmados porque estos estados no gaussianos nos permiten retener gran parte de los poderosos poderes matemáticos. maquinaria que existe para los estados gaussianos, al tiempo que nos permite describir un conjunto mucho más diverso de estados cuánticos", dice Bond.
"Hay tantos patrones posibles que las computadoras clásicas a menudo tienen dificultades para calcularlos y procesarlos. En cambio, en esta publicación utilizamos un método que identifica los más importantes de estos patrones e ignora los demás. Esto nos permite estudiar estos sistemas cuánticos y diseñar nuevas formas de preparar estados cuánticos interesantes."
El nuevo enfoque se puede aprovechar para preparar de manera eficiente estados cuánticos de una manera que supere a otros protocolos utilizados tradicionalmente. "La preparación rápida de estados cuánticos podría resultar útil para una amplia gama de aplicaciones, como la simulación cuántica o incluso la corrección de errores cuánticos", señala Bond.
Los investigadores también demuestran que pueden utilizar estados no gaussianos para preparar estados cuánticos "críticos" que corresponden a un sistema en transición de fase. Además del interés fundamental, estos estados pueden mejorar en gran medida la sensibilidad de los sensores cuánticos.
Si bien estos resultados son muy alentadores, son sólo un primer paso hacia objetivos más ambiciosos. Hasta ahora, el método se ha demostrado para un solo giro. Una extensión natural, pero desafiante, es incluir muchos giros y muchos modos bosónicos al mismo tiempo. Una dirección paralela debe tener en cuenta los efectos del entorno que perturba los sistemas de espín-bosones. Ambos enfoques están en desarrollo activo.