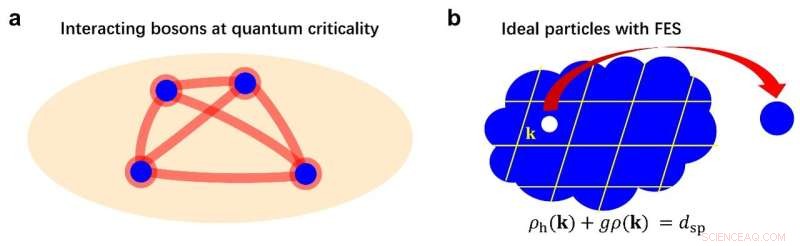
Materia crítica cuántica y estadística de exclusión fraccional. (a) Bosones que interactúan en la criticidad cuántica. (b) Partículas ideales con FES. Crédito:Science China Press
Un sistema cuántico que consta de un gran número de partículas microscópicas obedece leyes estadísticas a nivel macroscópico. En la naturaleza, hay dos tipos de partículas cuánticas microscópicas. Uno es el bosón que satisface las estadísticas de Bose-Einstein y el otro es el fermión que satisface las estadísticas de Fermi-Dirac.
Sin embargo, para los sistemas cuánticos que interactúan, estos dos tipos de estadísticas no son las únicas formas de estadísticas cuánticas. Por ejemplo, las estadísticas anónicas pueden surgir en electrones bidimensionales (2D). En 1991, el ganador del Premio Nobel de Física F. D. M. Haldane propuso un concepto novedoso de estadística de exclusión fraccional (FES), que es una distribución estadística generalizada, siendo las distribuciones de Bose y Fermi sus dos casos límite. En 1994, el físico Yongshi Wu y otros estudiaron las propiedades termodinámicas de los sistemas que satisfacen FES. Posteriormente, la teoría de la FES se ha utilizado para realizar estudios teóricos sobre el efecto Hall fraccional, gases cuánticos, modelos de espín, anyons y muchos otros problemas cuánticos de muchos cuerpos. Sin embargo, la observación de la FES en experimentos realistas sigue siendo difícil y escasa.
Los gases Bose unidimensionales con interacción repulsiva se han convertido en los últimos años en una plataforma importante para el estudio experimental de la física cuántica de muchos cuerpos. Se ha demostrado teóricamente que tales gases satisfacen la FES mutua en un espacio de cuasi impulso. Sin embargo, los acoplamientos entre diferentes cuasi-momentos hacen que sea muy difícil obtener una relación directa entre las cantidades físicas medibles y el parámetro estadístico.
Recientemente, Xibo Zhang y sus compañeros de trabajo descubrieron que para los gases de Bose cuánticos 1D y 2D en el régimen crítico cuántico, los acoplamientos entre los cuasi-momentos se vuelven bastante locales y surge un FES simple y no mutuo. Establecieron una correspondencia simple entre la fuerza de interacción y el parámetro estadístico. Con base en cálculos teóricos, simulaciones cuánticas numéricas de Monte Carlo y mediciones experimentales, los investigadores confirmaron que la entropía crítica por partícula y otras cantidades termodinámicas están determinadas por las de las partículas que no interactúan y obedecen a la FES.
Este estudio no solo proporciona una imagen física simple con evidencias teóricas, numéricas y experimentales de la aparición de FES en sistemas cuánticos que interactúan, sino que también brinda nuevas perspectivas y un método novedoso para comprender el comportamiento crítico de sistemas cuánticos de muchos cuerpos más complejos. , como gases cuánticos con simetrías SU(N), etc.
La investigación fue publicada en National Science Review . Cuantificación de los efectos de colisiones de tres partículas en gases cuánticos