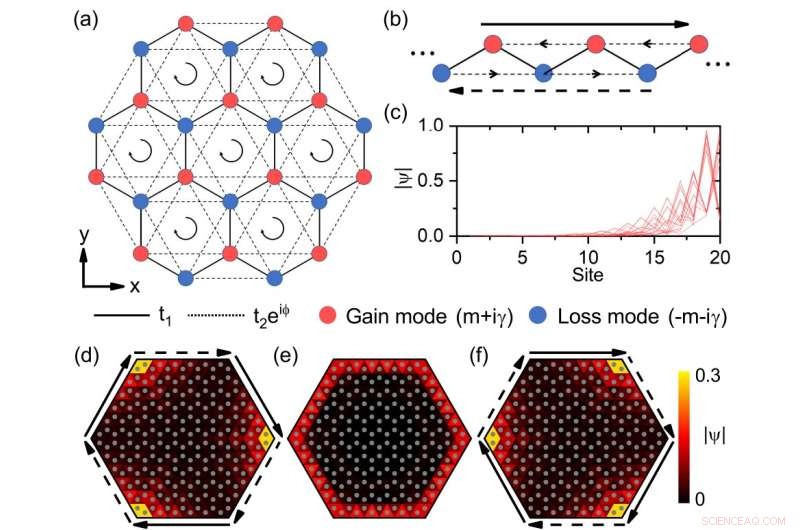
Descubrimiento de un efecto topológico de piel híbrido inducido por ganancia y pérdida

Fig. 1 Modos híbridos de piel y topología en el modelo de Haldane no hermitiano. (a) Esquema de la red no hermítica. Los círculos rojos (azules) indican sitios con términos de masa en el sitio opuestos +（m+iγ）. (b) Borde en zigzag de la red de panal como una cadena 1D, que tiene un efecto de piel no hermético con ganancia y pérdida en el sitio. La flecha sólida larga (discontinua) indica la corriente de borde quiral a lo largo (opuesta a) de la dirección localizada [similar en (d) y (f)]. Las flechas negras en (a) y las flechas de la línea media en (b) indican las direcciones de los acoplamientos del vecino más cercano t₂ e^iφ . ( c ) Perfil de todos los modos propios para la cadena 1D en ( b ) con 20 sitios. Las ganancias y pérdidas en el sitio son γ=3. (d)-(f) El modo de borde quiral para γ=0 (e) se convierte en modos topológicos de piel para γ=-0.6 (d) y γ=0.6 (f) con diferentes direcciones localizadas. Cada triángulo con un círculo gris denota un sitio. Aquí el modo de borde quiral se propaga en el sentido de las agujas del reloj. Crédito:Universidad de Tsinghua

Recientemente, el profesor asociado Yong-Chun Liu del Departamento de Física y otros han encontrado el efecto topológico de piel híbrido inducido por la ganancia y la pérdida y la transición de fase de tiempo de paridad entre los modos topológicos de piel. Los resultados de la investigación se publicaron en Physical Review Letters bajo el título de "Efecto topológico de piel híbrido inducido por ganancia-pérdida".

Los sistemas no hermitianos son sistemas abiertos que pueden ser descritos por hamiltonianos no hermitianos. Hay muchas propiedades novedosas en los sistemas no hermitianos, uno de los cuales es el efecto de piel no hermitiano. En este efecto, todos los estados propios de un sistema topológico (incluidos los estados masivos y los estados de borde) se localizan en uno de los límites del sistema, y la correspondencia convencional de borde masivo se descompone. Hay principalmente dos formas de realizar sistemas no hermitianos:una es usando acoplamientos no recíprocos y la otra usando ganancias y pérdidas.

En el caso de acoplamientos no recíprocos, la no hermiticidad proviene de la naturaleza no hermítica de la interacción entre diferentes sitios de red. El intercambio de energía entre los sitios de la red es asimétrico, por lo que hay un flujo de energía neto en una dirección y toda la energía finalmente se acumula en el límite. Así, los sistemas no recíprocos exhiben el efecto piel. En el caso de ganancia-pérdida, la no hermiticidad se origina en la ganancia y la pérdida en cada sitio de la red, lo que equivale a agregar energía imaginaria en el sitio a cada sitio de la red. Este tipo de sistema no hermitiano no siempre conduce al efecto piel. En sistemas realistas, los acoplamientos no recíprocos suelen ser difíciles de lograr, pero la disipación está muy extendida y la distribución de disipación escalonada es equivalente a ganancia y pérdida. Por lo tanto, es de gran importancia estudiar el efecto piel en sistemas no hermitianos de pérdida y ganancia.

Encontraron el efecto híbrido piel-topológico inducido por ganancia y pérdida en sistemas bidimensionales. Este tipo de efecto de piel es selectivo, es decir, los estados masivos y los estados de borde tienen un comportamiento diferente. Los estados de volumen no se ven afectados por el efecto de piel y permanecen extendidos, mientras que los estados de borde exhiben efecto de piel y se localizan más en las esquinas. Este fenómeno híbrido de efecto piel y efecto topológico muestra las propiedades únicas de los sistemas topológicos no hermitianos, que no tienen análogos hermitianos o no topológicos.

Como ejemplo específico, consideraron el modelo de Haldane no hermitiano con ganancias y pérdidas [Fig. 1 (a)]. En el modelo de Haldane, los estados de borde topológicos se obtienen introduciendo energía in situ y flujo magnético local. Es uno de los dos modelos importantes para realizar el efecto Hall cuántico anómalo en la física de la materia condensada. Descubrieron que si se introducen ganancias y pérdidas escalonadas en los sitios vecinos más cercanos en el modelo de Haldane, los modos de borde topológicos del sistema exhibirán el efecto de piel y se localizarán en las esquinas, mientras que los modos masivos no se verán afectados. Así, revela un efecto piel-topológico híbrido.

Al analizar los sitios de red en los bordes solo, este efecto topológico de piel de segundo orden se puede simplificar al efecto de piel de primer orden en los bordes. En el modelo unidimensional simplificado, hay corrientes de borde quirales debido al flujo magnético no local introducido por los acoplamientos complejos del vecino más cercano. Son equivalentes a los acoplamientos no recíprocos, por lo que el sistema presenta el efecto pelicular de primer orden [Fig. 1 (b)—(c)]. Por el contrario, sólo hay flujo local y la no reciprocidad se anula en la mayor parte del sistema. Por lo tanto, los modos masivos no se ven afectados por el efecto de piel. Al ajustar la ganancia y la pérdida del sistema, se puede cambiar la dirección de las corrientes de borde para controlar la dirección del efecto topológico de la piel [Fig. 1 (d)—(f)].

Además, obtuvieron la relación entre las simetrías de paridad-tiempo (PT) del sistema y el efecto topológico de piel híbrido. Al elegir la condición de frontera abierta y la condición de frontera periódica en diferentes direcciones, el sistema exhibe diferentes tipos de simetrías PT para diferentes tipos de bordes. La simetría PT global que mapea cualquier modo localizado en un límite en el otro límite impide la aparición del efecto topológico de piel híbrido, mientras que la simetría PT local con mapeo dentro de cada subcelda permite la existencia del efecto topológico de piel híbrido.

Por lo tanto, el análisis de las simetrías PT del sistema proporciona un medio simple y efectivo para juzgar si existe el efecto híbrido piel-topológico. En particular, encontraron que cuando la ganancia y la pérdida en el sistema aumentan, la transición de fase PT ocurrirá entre los modos topológicos de la piel, acompañada por la aparición de puntos excepcionales (EP). Cuando se rompe la simetría PT, las energías propias de los modos topológicos de la piel ya no son reales y las distribuciones de los modos propios correspondientes se vuelven PT asimétricas.

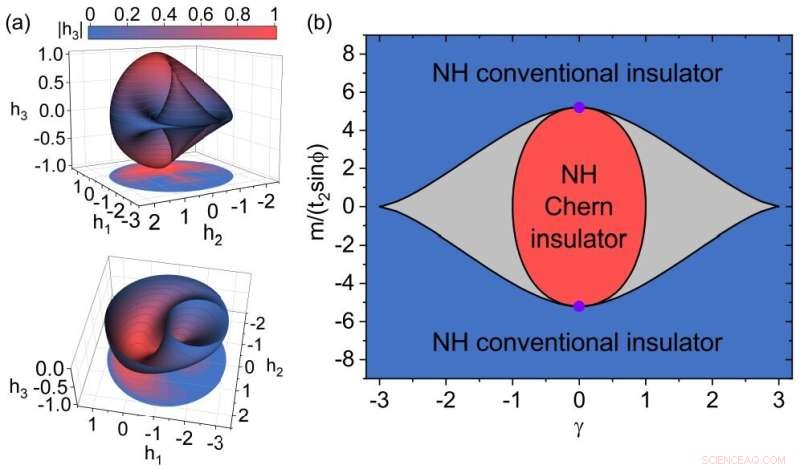
Fig. 2 The topology and phase diagram of the non-Hermitian Haldane model. (a) The surface S mapped from the first Brillouin zone, i.e., mapping from (k_x , k_y ) to (h₁ , h₂ , h₃ ). The color map represents the magnitude of h₃ . The density map below is the projection of the surface. The bottom figure is half of the top figure for h₃ <0. (b) The phase diagram. The red area is the non-Hermitian Chern insulator phase where C=1. The blue area is the non-Hermitian conventional insulator phase where C=0. The gray area is a gapless phase with EPs between two bulk bands. The black curves are phase boundaries. The purple points indicate the Hermitian phase boundary with the emergence of Dirac points. Credit:Tsinghua University

In addition, they studied the Chern numbers in the non-Hermitian system and obtained the phase diagram. They provided intuitionistic geometric meanings of the Chern numbers as topological invariants. As shown in Fig. 2(a), the two-dimensional Brillouin zone of the system can be mapped to a closed spherical surface S in the three-dimensional space, and the gap-closing points of the system form a circle L in the three-dimensional space. When the surface S encloses the circle L, the system is at the non-Hermitian Chern insulator phase, and the Chern number is 1, corresponding to the red region in Fig. 2(b). When the circle L is outside the surface S, the system is at the non-Hermitian conventional insulator phase, and the Chen number is 0, corresponding to the blue area in Fig. 2 (b). In the gray area in Fig. 2 (b), the system band gap is closed at six EPs.

The conclusion of this work is also applicable to the system with no gain and only pure dissipation. Dissipation is common in many physical systems, such as optical systems, atomic systems, and optomechanical systems. This work paves the way to realize non-Hermitian topological effect by gain and loss and study PT phase transition in higher-dimensional systems. It also provides attractive insights for potential applications in topological optics. + Explora más