
Crédito:CC0 Public Domain
En años recientes, computación de reservorio físico, una de las nuevas tecnologías de procesamiento de información, ha atraído mucha atención. Esta es una versión de implementación física de la computación de yacimientos, que es un método de aprendizaje derivado de la teoría de redes neuronales recurrentes (RNN). Implementa la computación al considerar el sistema físico como un enorme RNN, subcontratar las principales operaciones a la dinámica del sistema físico que forma el reservorio físico. Tiene la ventaja de obtener la optimización instantáneamente con recursos computacionales limitados ajustando las ponderaciones de lectura lineal y estática entre la salida y un depósito físico sin requerir la optimización de las ponderaciones por retropropagación.
Sin embargo, Dado que la capacidad de procesamiento de la información depende de la capacidad física del depósito, es importante que esto se investigue y optimice. Es más, al diseñar un depósito físico con alta capacidad de procesamiento de información, Se espera que el costo experimental se reduzca mediante simulación numérica. Ejemplos bien conocidos de computación de yacimientos físicos incluyen su aplicación a materiales blandos, fotónica, espintrónica, y cuantos, mientras que en los últimos años, se ha prestado mucha atención a las olas; Se han propuesto dispositivos neuromórficos que simulan funciones del cerebro mediante el uso de ondas no lineales.
El flujo fluido de agua, aire, etc. representa un sistema físico que es familiar pero muestra varios y complicados patrones que se ha pensado que tienen una alta capacidad de procesamiento de información. Sin embargo, La computación de yacimientos físicos virtuales mediante simulación numérica o investigación de la capacidad de procesamiento de información de los fenómenos de flujo de fluidos no se ha realizado debido a su costo computacional numérico relativamente alto. Por lo tanto, la relación entre el vórtice de flujo y la capacidad de procesamiento de información seguía siendo desconocida.
En este estudio, El profesor Hirofumi Notsu y un estudiante de posgrado de la Universidad de Kanazawa en colaboración con el profesor Kohei Nakajima de la Universidad de Tokio investigaron los fenómenos del flujo de fluidos como un sistema físico, especialmente el flujo de fluido que se produce alrededor de un cilindro, que se entiende bien. Se sabe que este sistema físico se rige por las ecuaciones incompresibles de Navier-Stokes, que describen el flujo de fluidos, y también incluye el número de Reynolds, un parámetro indicativo de las características del sistema.
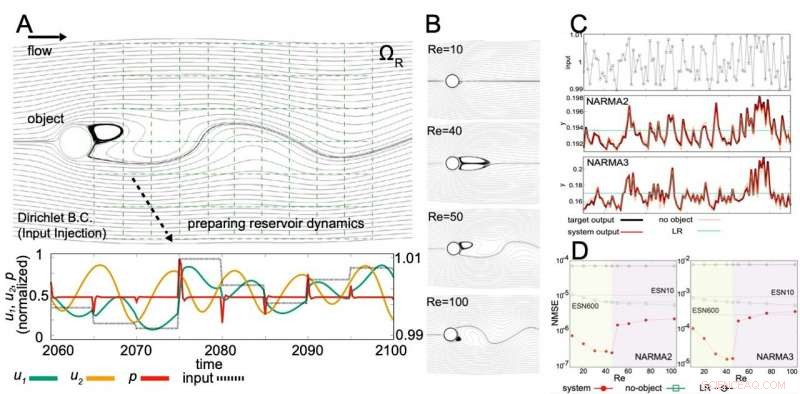
R:Esquema del estudio. B:Flujo de fluido típico en cada número de Reynolds. C:Entradas a lo largo de la secuencia de tiempo y los resultados de los modelos NARMA2 y NARMA3. Los valores objetivo están en negro, mientras que los valores de la computación de reservorios físicos virtuales usando vórtices están en rojo. D:Valores de errores (errores cuadráticos medios normalizados, NMSE) en cada número de Reynolds en los modelos NARMA2 y NARMA3. El error es mínimo y el número de Reynolds es de alrededor de 40. Crédito:Universidad de Kanazawa
Este sistema físico se implementó virtualmente mediante simulación numérica espacial bidimensional utilizando el método estabilizado de Lagrange-Galerkin, y la dinámica de la velocidad del flujo y la presión en los puntos seleccionados en la región aguas abajo del cilindro se utilizaron como depósito físico. La capacidad de procesamiento de información se evaluó mediante el modelo NARMA.
Se sabe que en el flujo de fluido alrededor de un cilindro, a medida que aumenta el valor del número de Reynolds, Los vórtices gemelos formados en la región aguas abajo del cilindro se hacen gradualmente más grandes y eventualmente forman una calle de vórtices Karman, el desprendimiento alternativo de vórtices. En este estudio, Se aclaró que en el número de Reynolds donde los vórtices gemelos son máximos pero justo antes de la transición a una calle de vórtices Karman, la capacidad de procesamiento de información es la más alta.
En otras palabras, antes de la transición a una calle de vórtice de Karman, la capacidad de procesamiento de información aumenta a medida que aumenta el tamaño de los vórtices gemelos. Por otra parte, Dado que la propiedad del estado de eco que garantiza la reproducibilidad de la computación del yacimiento no se puede mantener cuando se produce la transición a la calle del vórtice de Karman, queda claro que la calle del vórtice de Karman no se puede utilizar para la informática.
Se espera que estos hallazgos relacionados con los vórtices de flujo de fluidos y la capacidad de procesamiento de información sean útiles cuando, en el futuro, la capacidad de procesamiento de información del depósito físico se puede ampliar mediante el flujo de fluidos, p.ej. en el desarrollo de dispositivos neuromórficos basados en ondas reportados recientemente. Aunque el costo computacional numérico de los fenómenos de flujo de fluidos es relativamente alto, Este estudio ha permitido manejar vórtices macroscópicos que son físicamente fáciles de entender y ha aclarado la relación entre los vórtices y las capacidades de procesamiento de información al implementar virtualmente la computación física de yacimientos con simulación numérica espacial bidimensional.
Computación virtual de yacimientos físicos, que solía aplicarse a un número relativamente grande de sistemas físicos descritos como sistemas unidimensionales, se ha ampliado para incluir sistemas físicos con dos o más dimensiones espaciales. Se espera que los resultados de este estudio permitan la investigación virtual de las capacidades de procesamiento de información de una gama más amplia de sistemas físicos. Además, Dado que se revela que los vórtices son la clave para la capacidad de procesamiento de información, Se espera que se promueva aún más la investigación para crear o mantener vórtices.