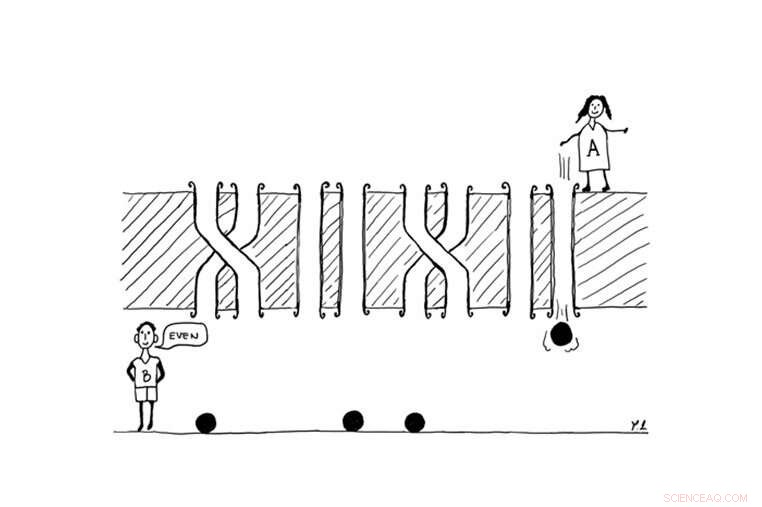
La figura muestra el ejemplo más simple de juegos de paridad. Alice (A) lanza una cierta cantidad de canicas hacia Bob (B), con el objetivo de saber si el número de tubos retorcidos es par o impar. Los jugadores necesitan cuatro canicas clásicas ordinarias para completar la tarea. A diferencia de, ya serían suficientes dos canicas cuánticas. Crédito:© Borivoje Dakić
Como dijo Richard Feynman, "El experimento de la doble rendija es absolutamente imposible de explicar de una manera clásica y tiene en él el corazón de la mecánica cuántica. En realidad, contiene el único misterio ".
En efecto, en este experimento, una partícula cuántica se comporta como si estuviera en dos ubicaciones distintas al mismo tiempo, y exhibe fenómenos similares a ondas paradigmáticos como la interferencia. Sin embargo, Más tarde se observó que los experimentos de múltiples rendijas muestran que el grado de deslocalización de las partículas cuánticas tiene sus límites, y que en cierto sentido, las partículas cuánticas no se pueden deslocalizar simultáneamente en más de dos ubicaciones. Esta limitación ha creado un rompecabezas que hasta el día de hoy aún no se ha resuelto por completo. Investigadores de la Universidad de Viena y la IQOQI-Viena (Academia de Ciencias de Austria) han dado un paso significativo hacia la comprensión de este problema al reformular los experimentos de interferencia en términos de juegos de teoría de la información. Su análisis, que ha aparecido recientemente en la revista Quantum, proporciona una forma intuitiva de pensar sobre los fenómenos de interferencia y sus limitaciones, allanando así el camino hacia la solución del rompecabezas antes mencionado.
Una de las características más llamativas de la mecánica cuántica es el principio de superposición. Este principio se puede ilustrar más fácilmente mediante el experimento de doble rendija, que involucra una partícula que se envía a través de una placa perforada con dos rendijas. De acuerdo con nuestras intuiciones cotidianas comunes, uno podría esperar que la partícula siempre pase a través de una rendija, oa través del otro. Sin embargo, La mecánica cuántica implica que la partícula puede, en cierto sentido, pasar por ambas rendijas al mismo tiempo, es decir, puede estar en una superposición de dos ubicaciones al mismo tiempo. Esta posibilidad subyace al fenómeno de la interferencia cuántica, es decir, el sorprendente comportamiento ondulatorio que presentan las partículas cuánticas. Ahora, ¿Hay alguna manera de cuantificar el grado en que las partículas cuánticas se pueden deslocalizar? ¿La teoría cuántica permite que las partículas recorran más de dos caminos al mismo tiempo? Para comprender estas preguntas, Los físicos han analizado "experimentos de múltiples rendijas, ", que difieren del experimento de doble rendija solo en el número de rendijas:por ejemplo, un experimento de triple rendija involucra una partícula enviada a través de tres rendijas.
Uno puede pensar que si una partícula cuántica puede pasar por dos rendijas al mismo tiempo, también debería poder pasar simultáneamente a través de tres, cuatro o cualquier número de ranuras. Asombrosamente, Inmediatamente se observó que cualquier patrón obtenido en experimentos con múltiples rendijas puede explicarse por el hecho de que la partícula siempre atraviesa como máximo dos rendijas al mismo tiempo. Aunque esta característica se entiende completamente matemáticamente, Las siguientes preguntas quedan sin respuesta:¿hay una razón física para la aparente asimetría entre el experimento de doble rendija y los experimentos de múltiples rendijas? ¿Qué subyace a esta limitación un tanto arbitraria de la "deslocalización" de las partículas cuánticas?
En su trabajo reciente, Sebastian Horvat y Borivoje Dakić, investigadores de la Universidad de Viena y IQOQI-Viena (Academia de Ciencias de Austria), han dado un paso significativo hacia la comprensión de este problema al abordarlo con la teoría de la información. A saber, han reformulado los fenómenos de interferencia y los experimentos de múltiples rendijas en términos de "juegos de paridad", el ejemplo más simple se ilustra en la figura. El juego involucra a dos jugadores, Alice y Bob, que están separados por una pared perforada con cuatro pares de tubos. Cada par de tubos puede ser rectos o retorcidos, y el número de pares trenzados es desconocido tanto para Alice como para Bob. Es más, Alice tiene a disposición una cierta cantidad de canicas que puede hojear a través de los tubos hacia Bob; los jugadores pueden usar estas canicas para aprender algo sobre la estructura de los tubos.
El objetivo del juego es que los jugadores cooperen y averigüen si el número total de pares trenzados es par o impar. utilizando la menor cantidad posible de canicas. Ahora, supongamos que Alice lanza una canica a través de uno de los tubos, por ejemplo a través del segundo. Bob puede entonces inferir fácilmente si el primer par de tubos es recto o retorcido simplemente verificando si la canica ha caído por el segundo tubo o por el primero. Análogamente, si Alice tiene a disposición cuatro canicas, puede pasar cada uno de ellos a través del tubo derecho de cada par (como es el caso en la figura). Bob puede inferir directamente el número de pares trenzados, y, por tanto, si este número es par o impar, ganando así el juego. Sin embargo, si el número de pares de tubos excede el número de canicas que Alice tiene a disposición, entonces el juego no se puede ganar, ya que siempre habrá al menos un par de tubos, sobre lo cual Bob no puede recopilar información alguna. Por lo tanto, para ganar el juego, los jugadores deben usar tantas canicas como pares de tubos.
Por otra parte, mecánica cuántica, y mas especificamente, el principio de superposición, permite a los jugadores ganar el juego ilustrado en la figura utilizando solo dos "canicas cuánticas". Una forma de entender de dónde proviene esta mejora es recordar:como se dijo anteriormente, que una partícula cuántica puede "pasar por dos lugares al mismo tiempo". Por lo tanto, dos canicas cuánticas pueden "pasar simultáneamente a través de cuatro ubicaciones", imitando así el comportamiento de cuatro canicas ordinarias (clásicas). "En este juego, Las canicas se comportan de manera análoga a las fichas que se pueden insertar a través de los tubos. Cuando Alice inserta una canica clásica ordinaria, es como si hubiera insertado 1 centavo.
Por otra parte, como la teoría cuántica permite que las canicas "pasen a través de 2 tubos al mismo tiempo", cada canica cuántica vale 2 centavos. El valor de los tokens es aditivo:por ejemplo, para ganar el juego, Alice puede insertar 4 canicas clásicas o 2 canicas cuánticas, ya que el valor total del token es en ambos casos igual a 4 centavos ", explica Sebastian Horvat. Por otra parte, recuerde que una partícula cuántica no puede atravesar más de dos ubicaciones al mismo tiempo:esto se refleja en el hecho de que Alice y Bob no pueden ganar el juego usando menos de dos canicas cuánticas. Por eso, para ganar el juego, el número de canicas cuánticas enviadas por Alice debe ser igual al menos a la mitad del número total de pares de tubos.
En su trabajo, los investigadores han analizado formulaciones más generales de este juego y han estudiado el rendimiento de los jugadores en función del número de partículas y de si las partículas son clásicas, cuántico, o de tipos más generales e hipotéticos. Borivoje Dakić añade:"Estas partículas hipotéticas poseen un mayor poder de procesamiento de información, es decir, sus fichas correspondientes son válidas más de 2 centavos. No está claro por qué la naturaleza debería preferir las partículas clásicas y cuánticas a estas hipotéticas:esto es algo que todavía tenemos que estudiar en el futuro ".
Considerándolo todo, Los juegos de paridad proporcionan una descripción alternativa de la interferencia cuántica dentro de un marco más general e intuitivo, que, con suerte, arrojará luz sobre las características novedosas de la superposición cuántica, de manera similar a cómo se ha profundizado el estudio del entrelazamiento cuántico a través de la formulación de los llamados "juegos no locales".