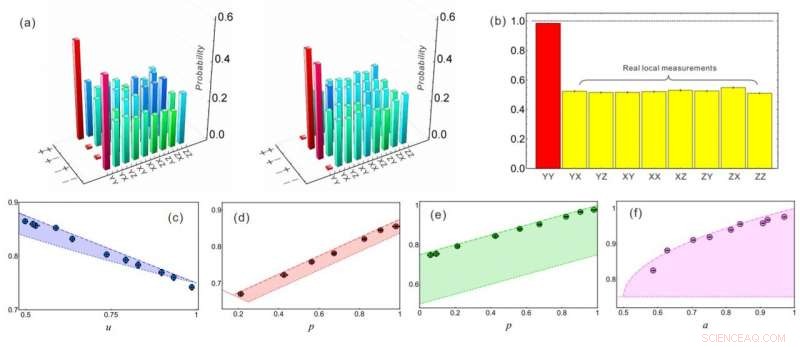
Resultados experimentales para la discriminación del estado local. Crédito:WU Kangda et al.
Recientemente, un equipo de investigación dirigido por el académico Guo Guangcan del Laboratorio Clave de Información Cuántica de la Universidad de Ciencia y Tecnología de China (USTC) de CAS, ha logrado importantes avances en la teoría de la información cuántica. El profesor Li Chuanfeng y el profesor Xiang Guoyong del equipo colaboraron con el Dr. Strelstov de la Universidad de Varsovia para investigar la parte imaginaria de la teoría cuántica como recurso. y se han obtenido varios resultados importantes. Los resultados relevantes ahora se publican conjuntamente como sugerencia de los editores en Cartas de revisión física y Revisión física A .
Un número complejo es una herramienta matemática, y es muy utilizado en mecánica, electrodinámica, óptica y otros campos relacionados de la física para proporcionar una elegante formulación de la teoría correspondiente. El nacimiento de la mecánica cuántica da una imagen unificada de onda y partícula, y refuerza aún más el papel destacado de los números complejos en la física. Sin embargo, La cuestión de si las estructuras complejas son necesarias para la mecánica cuántica ha sido debatida durante mucho tiempo por los físicos.
Los investigadores han considerado el número complejo como una especie de recurso cuántico, y revelar su papel insustituible en la discriminación local de estados cuánticos bipartitos. Es más, en el marco de la teoría cuántica de recursos, estudiaron el método de medición de este recurso y el problema de transformación bajo diversas operaciones libres. Han resuelto el problema de la medición de robustez de tamaño complejo, transformación del estado cuántico de un solo bit en funcionamiento libre, y probabilidad de transformación mutua de cualquier estado puro en funcionamiento libre.
Usando el estado entrelazado de dos fotones preparado por conversión descendente paramétrica, Además, los investigadores midieron y compararon la probabilidad de éxito de distinguir localmente el estado cuántico cuando solo usaban la base de medición real y la base de medición general. Observaron con éxito el aumento de la probabilidad de éxito al utilizar la base de medición compleja, que verificó el importante papel del complejo en la mecánica cuántica.
Este trabajo prueba que la parte imaginaria es indispensable en la teoría de la mecánica cuántica. El revisor lo recomendó encarecidamente, señalando "Encuentro que el imaginario cuántico puede considerarse como una forma más fuerte de coherencia cuántica ... También creo que los resultados del manuscrito estimularán la investigación sobre la base cuántica y las teorías cuánticas de recursos con una estructura más rica".