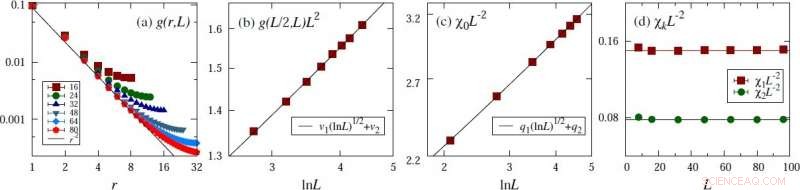
Evidencia de la forma de escala conjeturada en el ejemplo del modelo crítico 4D XY. (a) Función de correlación de dos puntos. (b) Correlación de dos puntos a la distancia de la mitad del tamaño del sistema lineal. (c) Susceptibilidad magnética. (d) Fluctuaciones magnéticas en modos de Fourier distintos de cero. Crédito:© Science China Press
Desde el establecimiento de la teoría de grupos de renormalización, Se ha sabido que los sistemas de fenómenos críticos típicamente poseen una dimensión crítica superior dc (dc =4 para el modelo O (n)), tal que en dimensiones espaciales iguales o superiores a la cd, el comportamiento termodinámico se rige por exponentes críticos que toman valores de campo medio. En contraste con la simplicidad del comportamiento termodinámico, la teoría de la escala de tamaño finito (FSS) para el d> El modelo dc O (n) era sorprendentemente sutil y había sido objeto de un debate en curso hasta hace poco. cuando se conjeturaba un ansatz de escala de dos longitudes para la función de correlación de dos puntos, confirmado numéricamente, y apoyado en parte por cálculos analíticos.
En la dimensionalidad crítica superior dc, Las correcciones logarítmicas multiplicativas y aditivas generalmente ocurren en el comportamiento de campo medio desnudo. La aclaración de las correcciones logarítmicas en FSS se vuelve 'notoriamente difícil, 'debido a la falta de conocimientos analíticos más allá del nivel fenomenológico y al límite de tamaños de sistemas disponibles en simulaciones numéricas. La forma logarítmica precisa de FSS en d =dc sigue siendo un problema de larga data.
Recientemente, Jian-Ping Lv, Wanwan Xu, y Yanan Sun de la Universidad Normal de Anhui, Kun Chen de Rutgers, la Universidad Estatal de Nueva Jersey, y Youjin Deng de la Universidad de Ciencia y Tecnología de China y la Universidad de Minjiang abordaron el FSS logarítmico de la simetría O (n) en la dimensionalidad crítica superior. Tomando prestados conocimientos de dimensiones superiores, establecieron una forma de escala explícita para la densidad de energía libre, que consiste simultáneamente en un término de escala para el punto fijo gaussiano y otro término con correcciones logarítmicas multiplicativas. En particular, Conjeturaron que la correlación de dos puntos crítica de tamaño finito exhibe un comportamiento de dos longitudes, que se rige por un punto fijo gaussiano a una distancia más corta, y entra en una meseta a una distancia mayor cuya altura disminuye con el tamaño del sistema en una ley de potencia corregida por un exponente logarítmico.
Sobre esta base, Se predijo la FSS de varias cantidades macroscópicas. Luego llevaron a cabo extensas simulaciones de Monte Carlo para el modelo de n-vector con n =1, 2, 3, y obtuvo evidencia sólida que respalda las formas de escala conjeturadas del FSS de la susceptibilidad, las fluctuaciones magnéticas en modos de Fourier distintos de cero, el aglutinante acumulativo, así como la correlación de dos puntos a la distancia de la mitad del tamaño del sistema lineal. Este es un paso significativo hacia una solución completa del SFS logarítmico en d =dc para sistemas que tienen una dimensionalidad crítica superior.
El estudio no solo es de importancia teórica en los sistemas modelo, sino también de relevancia práctica para un gran número de sistemas experimentales. Se observa que debido a los desarrollos tecnológicos, la realización experimental del modelo O (n) ahora está disponible en varios sistemas físicos, incluidos los materiales magnéticos cuánticos, Matrices de unión de Josephson, y sistemas atómicos ultrafríos. Según el mapeo cuántico a clásico, los sistemas cuánticos tridimensionales O (n) se encuentran en la dimensionalidad crítica superior.