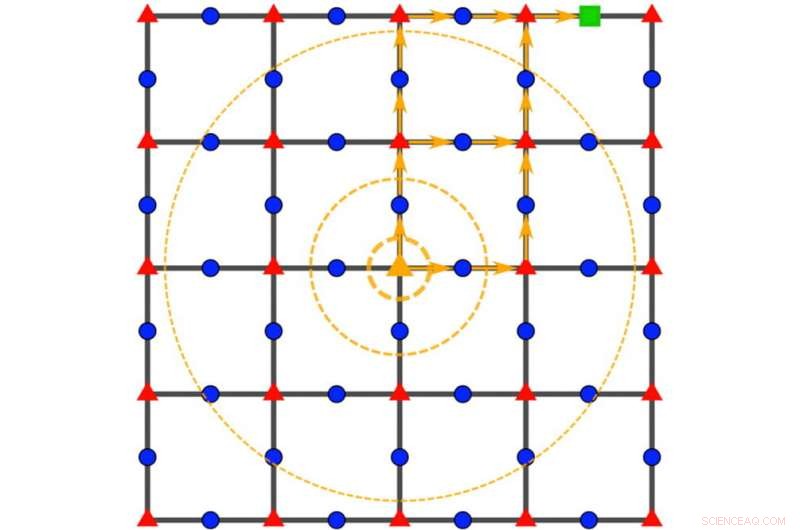
Un gráfico de conmutatividad de Wang-Hazzard captura el detalle microscópico de las funciones matemáticas que los físicos suelen utilizar para describir la energía en sistemas cuánticos. reduciendo el cálculo de los límites de velocidad cuántica a una ecuación con solo dos entradas. Crédito:Zhiyuan Wang / Universidad Rice
Los límites de velocidad de la naturaleza no están publicados en las señales de tráfico, pero los físicos de la Universidad de Rice han descubierto una nueva forma de deducirlos que es mejor, infinitamente mejor, en algunos casos, que los métodos anteriores.
"La gran pregunta es, '¿Qué tan rápido puede cualquier cosa, información, masa, energía, ¿moverse en la naturaleza? '", dijo Kaden Hazzard, un físico cuántico teórico en Rice. "Resulta que si alguien te entrega un material, es increiblemente dificil, en general, para responder a la pregunta ".
En un estudio publicado hoy en la revista American Physical Society PRX Quantum , El estudiante graduado de Hazzard y Rice, Zhiyuan Wang, describe un nuevo método para calcular el límite superior de los límites de velocidad en la materia cuántica.
"A un nivel fundamental, estos límites son mucho mejores que los que estaban disponibles anteriormente, "dijo Hazzard, profesor asistente de física y astronomía y miembro del Centro Rice de Materiales Cuánticos. "Este método genera con frecuencia límites que son 10 veces más precisos, y no es inusual que sean 100 veces más precisos. En algunos casos, la mejora es tan espectacular que encontramos límites de velocidad finitos donde los enfoques anteriores predijeron infinitos ".
El límite máximo de velocidad de la naturaleza es la velocidad de la luz, pero en casi todo lo que nos rodea, la velocidad de la energía y la información es mucho más lenta. Frecuentemente, Es imposible describir esta velocidad sin tener en cuenta el gran papel de los efectos cuánticos.
En los 1970s, Los físicos demostraron que la información debe moverse mucho más lento que la velocidad de la luz en materiales cuánticos, y aunque no pudieron calcular una solución exacta para las velocidades, Los físicos Elliott Lieb y Derek Robinson fueron pioneros en métodos matemáticos para calcular los límites superiores de esas velocidades.
"La idea es que, incluso si no puedo decirte la velocidad máxima exacta, ¿Puedo decirte que la velocidad máxima debe ser menor que un valor particular, "Hazzard dijo." Si puedo dar una garantía del 100% de que el valor real es menor que ese límite superior, eso puede ser extremadamente útil ".
Hazzard dijo que los físicos saben desde hace mucho tiempo que algunos de los límites producidos por el método Lieb-Robinson son "ridículamente imprecisos".
"Podría decir que la información debe moverse a menos de 100 millas por hora en un material cuando la velocidad real se midió a 0,01 millas por hora, ", dijo." No está mal, pero no es muy útil ".
Los límites más precisos descritos en el artículo PRX Quantum se calcularon mediante un método creado por Wang.
"Inventamos una nueva herramienta gráfica que nos permite tener en cuenta las interacciones microscópicas en el material en lugar de depender solo de propiedades más crudas, como su estructura reticular, "Dijo Wang.
Hazzard dijo Wang, un estudiante de tercer año de posgrado, tiene un talento increíble para sintetizar relaciones matemáticas y reformularlas en nuevos términos.
"Cuando reviso sus cálculos, Puedo ir paso a paso revise los cálculos y compruebe que son válidos, ", Dijo Hazzard." Pero para descubrir cómo llegar del punto A al punto B, qué conjunto de pasos tomar cuando hay una variedad infinita de cosas que puede probar en cada paso, la creatividad es simplemente asombrosa para mí ".
El método Wang-Hazzard se puede aplicar a cualquier material hecho de partículas que se muevan en una red discreta. Eso incluye materiales cuánticos frecuentemente estudiados como superconductores de alta temperatura, materiales topológicos, fermiones pesados y otros. En cada uno de estos, el comportamiento de los materiales surge de interacciones de miles de millones y miles de millones de partículas, cuya complejidad está más allá del cálculo directo.
Hazzard dijo que espera que el nuevo método se utilice de varias formas.
"Además de la naturaleza fundamental de esto, podría ser útil para comprender el rendimiento de las computadoras cuánticas, en particular para comprender cuánto tardan en resolver problemas importantes en materiales y química, " él dijo.
Hazzard dijo que está seguro de que el método también se utilizará para desarrollar algoritmos numéricos porque Wang ha demostrado que puede poner límites rigurosos a los errores producidos por técnicas numéricas de uso frecuente que se aproximan al comportamiento de sistemas grandes.
Una técnica popular que los físicos han utilizado durante más de 60 años es aproximar un sistema grande a uno pequeño que pueda ser simulado por una computadora.
"Dibujamos una pequeña caja alrededor de un fragmento finito, simular eso y esperar que sea suficiente para aproximarse al gigantesco sistema, ", Dijo Hazzard." Pero no ha habido una forma rigurosa de delimitar los errores en estas aproximaciones ".
El método de Wang-Hazzard para calcular los límites podría conducir precisamente a eso.
"Existe una relación intrínseca entre el error de un algoritmo numérico y la velocidad de propagación de la información, Wang explicó, utilizando el sonido de su voz y las paredes de su habitación para ilustrar el vínculo.
"El fragmento finito tiene bordes, así como mi habitación tiene paredes. Cuando hablo, el sonido se reflejará en la pared y me devolverá el eco. En un sistema infinito no hay borde, por lo que no hay eco ".
En algoritmos numéricos, los errores son el equivalente matemático de los ecos. Reverberan desde los bordes de la caja finita, y la reflexión socava la capacidad de los algoritmos para simular el caso infinito. La información más rápida se mueve a través del sistema finito, cuanto menor sea el tiempo, el algoritmo representa fielmente el infinito.
Hazzard dijo que él Wang y otros en su grupo de investigación están utilizando su método para crear algoritmos numéricos con barras de error garantizadas.
"Ni siquiera tenemos que cambiar los algoritmos existentes para ponerlos estrictos, barras de error garantizadas en los cálculos, ", dijo." Pero también puedes darle la vuelta y usar esto para hacer mejores algoritmos numéricos. Estamos explorando eso y otras personas también están interesadas en utilizarlas ".