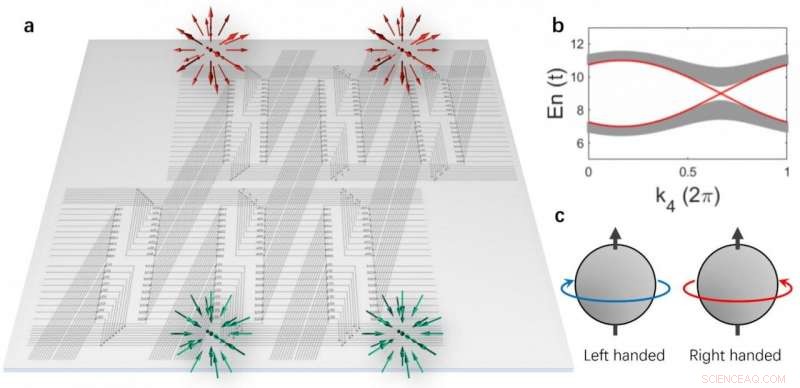
(a) La celosía del circuito 4D realizada en un plano 2D. Un par de puntos de Weyl con la misma quiralidad se localizan en el límite tridimensional. (b) Las estructuras de bandas de volumen y los estados de frontera de Weyl (líneas rojas). (c) Esquema de la quiralidad de los estados de Weyl. Crédito:Science China Press
En años recientes, La topología ha surgido como una herramienta importante para clasificar y caracterizar las propiedades de los materiales. Se ha encontrado que muchos materiales exhiben una serie de propiedades topológicas inusuales, que no se ven afectados por deformaciones, p.ej., extensión, apresamiento, o retorciéndose. Estas propiedades topológicas incluyen corrientes Hall cuantificadas, gran magnetorresistencia, y excitaciones superficiales que son inmunes al desorden. Se espera que estas propiedades puedan utilizarse para tecnologías futuras, tal como, electrónica de baja potencia, detectores ultrarrápidos, convertidores de energía de alta eficiencia, o para computación cuántica.
Más recientemente, La topología se ha aplicado también a materiales sintéticos, p.ej., Cristales fotónicos o redes de circuitos eléctricos. Estos materiales sintéticos tienen varios beneficios en comparación con sus contrapartes naturales. Por ejemplo, la topología de sus excitaciones (es decir, sus bandas de excitación) se pueden controlar y manipular con precisión. Además, debido a su conectividad de celosía de largo alcance, los materiales sintéticos pueden realizar excitaciones topológicas en dimensiones superiores a tres. Por eso, materiales sintéticos, y en particular redes de circuitos eléctricos, ofrecen la posibilidad de realizar una serie de propiedades topológicas interesantes que no son accesibles en materiales reales.
Rui Yu de la Universidad de Wuhan, Yuxin Zhao de la Universidad de Nanjing, y Andreas Schnyder del Max-Planck-Institute Stuttgart ahora han demostrado este potencial al construir explícitamente una red de circuito eléctrico que simula un aislante topológico de cuatro dimensiones (4-D) con una simetría clásica de inversión del tiempo [Fig. 1 (a)]. Los aislantes topológicos son materiales que son aislantes en el volumen a granel, pero muy conductivo en la superficie, debido a excitaciones superficiales sin espacios. Similar, el aislante topológico 4-D simulado tiene un espacio de excitación en el volumen total, dentro del cual existe un par de excitaciones superficiales [Fig. 1 (b)].
Estas excitaciones superficiales tridimensionales tienen una dispersión lineal, y más interesante, son del tipo Weyl con la misma mano, es decir., tienen grados internos de libertad que están girando siguiendo la misma regla de la mano izquierda o derecha con respecto a su dirección de propagación [Fig. 1 (c)]. Son de origen topológico y no se parecen a ninguna excitación superficial encontrada en materiales convencionales. La topología dicta que estas excitaciones de Weyl 3-D deben venir en pares y que son resistentes al desorden y las deformaciones. Los autores han realizado simulaciones numéricas detalladas de la red de circuitos topológicos y han demostrado que las excitaciones de Weyl 3-D se pueden observar fácilmente en mediciones dependientes de la frecuencia.
El trabajo de los autores demuestra que las excitaciones topológicas se pueden realizar fácilmente en placas de circuito disponibles comercialmente o en obleas de circuito integrado compuestas por inductores y condensadores. Allana el camino para realizar tipos arbitrarios de excitaciones superficiales topológicas, por ejemplo, las llamadas excitaciones de Dirac o Majorana de dos dimensiones, Tres, o incluso más. La implementación de circuitos eléctricos de excitaciones topológicas tiene la ventaja de ser simple, fácilmente reconfigurable, y permitiendo un alto grado de control. Esto permitirá estudiar en el futuro las transiciones de fase topológica, efectos no lineales, fenómenos de desequilibrio, y sistemas abiertos cuánticos (por ejemplo, sistemas no hermitianos).