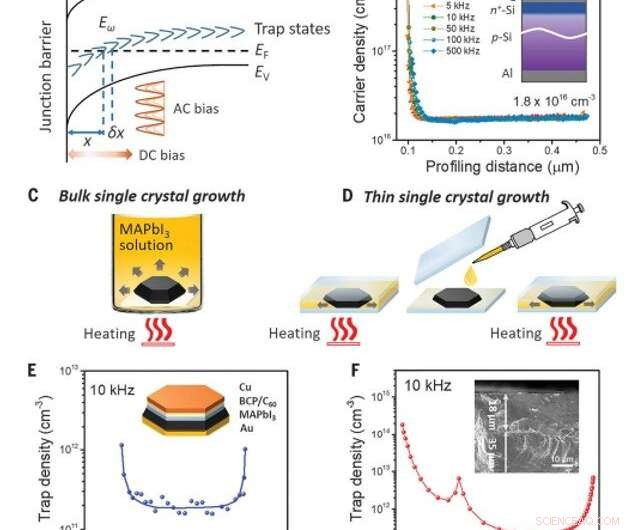
Técnica DLCP. (A) Esquema de flexión de banda de un semiconductor de tipo p con estados de trampa profunda en una unión n + -p. X denota la distancia desde la barrera de unión donde las trampas pueden cambiar dinámicamente sus estados de carga con la polarización de CA dV. dX denota el cambio diferencial de X con respecto a dV. Ew es la energía de demarcación determinada por Ew =kTln (w0 / w) (donde k es la constante de Boltzmann). CE, EV, y EF indican el borde de la banda de conducción, borde de la banda de valencia, y nivel de Fermi, respectivamente. (B) Dependencia de la densidad del portador de la distancia de perfil de una celda solar de Si a diferentes frecuencias de CA medidas por DLCP. El recuadro muestra el esquema de la estructura del dispositivo. (C) Esquema de la síntesis de un monocristal de MAPbI3 a granel en una solución al aire libre. (D) Esquema de la síntesis de un monocristal delgado de doble capa MAPbI3 utilizando el método de crecimiento de espacio confinado. (E) Dependencia de la densidad de la trampa en la distancia de perfil de un monocristal MAPbI3 medido por DLCP. El recuadro muestra la estructura del dispositivo. (F) Dependencia de la densidad de la trampa de la distancia de perfilado de un monocristal delgado de doble capa MAPbI3. El recuadro muestra la imagen SEM en sección transversal del monocristal delgado MAPbI3 de doble capa. Los espesores de los monocristales superior e inferior eran de 18 y 35 mm, respectivamente. Crédito:Ciencia, doi:10.1126 / science.aba0893
En un nuevo informe publicado el Ciencias , Zhenyi Ni y un equipo de investigación en ciencias físicas aplicadas, La ingeniería mecánica y de materiales y la ingeniería informática y energética en los EE. UU. perfilaron distribuciones espaciales y energéticas de estados de trampa o defectos en células solares policristalinas monocristalinas de perovskita de haluro metálico. Los investigadores atribuyeron el rendimiento fotovoltaico de las perovskitas de haluro metálico (MHP) a su alto coeficiente de absorción óptica, movilidad del portador, longitud de difusión de carga larga y energía de Urbach pequeña (que representa el desorden en el sistema). Los estudios teóricos han demostrado la posibilidad de formar trampas de carga profundas en la superficie del material debido a la baja energía de formación, defectos estructurales y límites de grano de perovskitas para guiar el desarrollo de técnicas de pasivación (pérdida de reactividad química) en células solares de perovskita. Los estados de la trampa de carga juegan un papel importante durante la degradación de las células solares de perovskita y otros dispositivos. Comprender la distribución de los estados de las trampas en su espacio y energía puede aclarar el impacto de las trampas de carga (defectos) en el transporte de carga en los materiales y dispositivos de perovskita para su rendimiento óptimo.
Los científicos han utilizado ampliamente la espectroscopia de admitancia térmica (TAS) y los métodos de corriente estimulada térmicamente (TSC) para medir la densidad de estados de trampa dependiente de la energía (tDOS) dentro de las células solares de perovskita. Por lo general, los métodos pueden alcanzar una profundidad de trampa de aproximadamente 0,55 eV, lo suficientemente profunda para producir células solares eficientes. Para detectar estados de trampa más profundos que existen dentro de las perovskitas de banda ancha, Los investigadores han utilizado técnicas como la espectroscopia de fotovoltaje de superficie y la fotocorriente de subbanda. Sin embargo, la mayoría de las técnicas no se pueden aplicar a dispositivos solares ya terminados para medir la distribución espacial de los estados de trampa. En este trabajo, Ni et al. demostraron el método de perfil de capacitancia a nivel de unidad (DLCP), una técnica alternativa basada en capacitancia para proporcionar distribuciones espaciales bien caracterizadas de densidades de portadora y trampa en perovskitas. Los científicos mapearon la distribución espacial y energética de los estados de trampa dentro de los monocristales de perovskita y las películas delgadas policristalinas para una comparación sencilla.
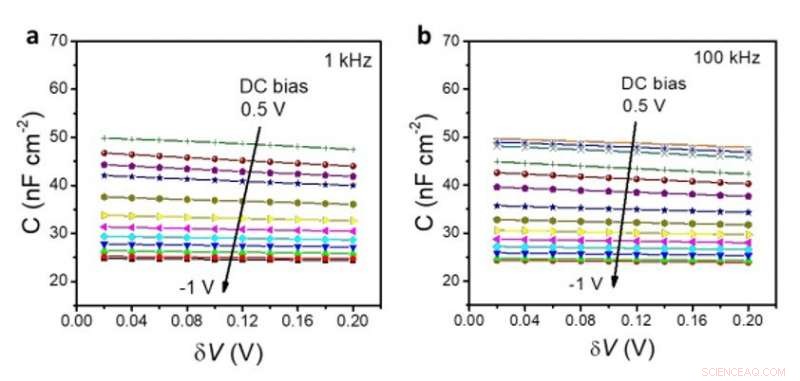
Variación de la capacitancia de la unión con la amplitud de las polarizaciones de CA para una celda solar de Si. Variación de la capacitancia de unión (C) de una celda solar de Si con respecto a la amplitud de las polarizaciones de CA (δV) bajo diferentes polarizaciones de CC medidas en frecuencias de CA de (a) 1 kHz y (b) 100 kHz. Crédito:Ciencia, doi:10.1126 / science.aba0893
El equipo desarrolló el método DLCP (perfil de capacitancia a nivel de unidad) para estudiar la distribución espacial de defectos en la banda prohibida de semiconductores amorfos y policristalinos como el silicio amorfo. El método podría determinar directamente la densidad de portadora para incluir tanto la densidad de portadora libre como la densidad de trampa dentro de la banda prohibida de los semiconductores, así como su distribución en el espacio y la energía. Estimaron la densidad de la trampa restando la densidad de portadora libre estimada medida a altas frecuencias de corriente alterna (CA) de la densidad de portadora total medida a baja frecuencia de CA. La técnica permitió al equipo derivar la distribución energética de los estados de trampa. Para validar la precisión de la densidad de portadora medida con el método DLCP, Los científicos realizaron mediciones de DLCP en una celda solar de silicio fabricada en una oblea de Si (p-Si) cristalino de tipo p con una capa de difusión de tipo n Si (n + ) encima. La medición fue consistente con la concentración de dopante de la oblea de p-Si obtenida de la medición de la conductividad para validar la precisión de la densidad del portador medida usando DLCP.
Para perfilar las densidades de portadora y trampa usando DLCP, Los investigadores investigaron a través de un dispositivo desde un electrodo hasta el contraelectrodo para comprender la ubicación de las uniones en las células solares de perovskita de estructura plana. El equipo llevó a cabo varios experimentos y observó que las células de perovskita normalmente mantenían una n + -P unión entre componentes del dispositivo. Para determinar la profundidad del perfil correspondiente a la profundidad física del material, Ni et al. construyó un dispositivo que contiene una doble capa de yoduro de plomo de metil amonio (MAPbI 3 ) cristales delgados para localizar las trampas de carga. Cuando perfilaron la densidad de trampas del dispositivo diseñado, obtuvieron un pico en la densidad de la trampa a una distancia de perfil de 18 µm.
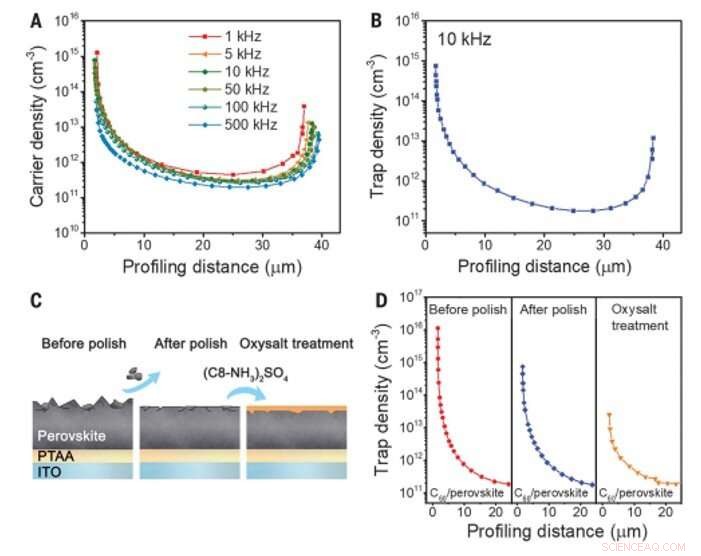
Distribuciones espaciales de los estados de la trampa en un monocristal delgado MAPbI3. (A) Dependencia de la densidad del portador de la distancia de perfil de un monocristal delgado MAPbI3 de 39 mm de espesor a diferentes frecuencias de CA, medido por DLCP. (B) Dependencia de la densidad de la trampa de la distancia de perfil de un monocristal delgado MAPbI3 medido a una frecuencia de CA de 10 kHz. La densidad de portadora medida a 500 kHz se considera portadora libre. (C) Esquemas de un monocristal delgado MAPbI3 en un sustrato PTAA / ITO antes del pulido mecánico, después del pulido mecánico, y después del tratamiento con oxisal [(C8 – NH3) 2SO4]. (D) Densidad de la trampa cerca de la barrera de unión de un monocristal delgado MAPbI3 antes del pulido mecánico, después del pulido mecánico, y después del tratamiento con oxisal. Crédito:Ciencia, doi:10.1126 / science.aba0893
Luego, el equipo estudió la distribución de la trampa en las células solares de cristal único de perovskita y observó la mayor eficiencia de conversión de energía (PCE) del primer MAPbI informado. 3 celda solar monocristalina en sólo el 17,9 por ciento; mucho más bajo que el de las células solares policristalinas. No eran conscientes del mecanismo subyacente que limitaba la difusión del portador en cristales delgados y realizaron mediciones de DLCP para investigar la relación entre la densidad de trampas y las distribuciones de trampas utilizando métodos de cristal sintético. El equipo observó la distribución espacial de las densidades de portadores a lo largo de un MAPbI típico. 3 cristal único fino, que sintetizaron utilizando un método de crecimiento de espacio confinado a diferentes frecuencias, y notó un aumento de la densidad de portadora con la disminución de la frecuencia de CA, indicando la existencia de trampas de carga en el MAPbI 3 cristal único fino.
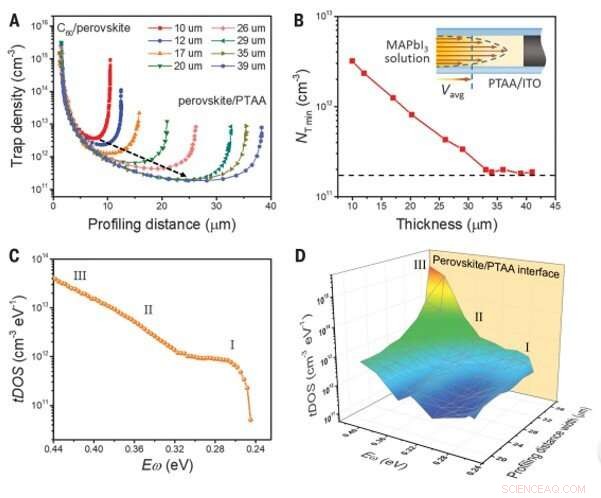
Distribuciones de densidad de trampas dependientes del espesor en monocristales delgados de MAPbI3. (A) Dependencia de las densidades de la trampa de las distancias de perfilado de monocristales delgados MAPbI3 con diferentes espesores de cristal medidos a una frecuencia de CA de 10 kHz. La ubicación de la interfaz MAPbI3 / C60 para cada cristal se alinea para comparar. La flecha de trazos negros indica la tendencia del cambio de la densidad de trampa mínima NT min en monocristales de MAPbI3 con diferentes espesores. (B) Dependencia de la NT min en el monocristal delgado MAPbI3 del espesor del cristal. La línea discontinua horizontal indica el valor mínimo de NT en un monocristal de MAPbI3 a granel. El recuadro muestra un esquema del flujo laminar de la solución precursora entre dos vasos de PTAA / ITO durante el crecimiento del cristal. Las flechas indican la dirección del flujo laminar de la solución precursora, y la longitud de la flecha denota la velocidad del flujo laminar. (C) tDOS de un monocristal delgado MAPbI3, medido por el método TAS. El espesor del monocristal delgado MAPbI3 fue de 39 mm. (D) Mapeo espacial y energético de las densidades de los estados de trampa en el monocristal delgado MAPbI3, medido por DLCP. Crédito:Ciencia, doi:10.1126 / science.aba0893
Para comprender el origen de la densidad de trampa profunda en la interfaz de perovskita, El equipo utilizó microscopía electrónica de transmisión de alta resolución y examinó muestras de perovskita de diferentes composiciones. Compararon las distribuciones de densidad de la trampa entre los monocristales de perovskita y las películas delgadas policristalinas con diferentes composiciones. Las distribuciones de densidad de la trampa para los monocristales delgados fueron varios órdenes de magnitud más bajas que las de las películas delgadas policristalinas. Los resultados mostraron la importancia de los procesos adecuados de modificación de la superficie para reducir las densidades de captura en los monocristales de perovskita en la interfaz de las películas delgadas policristalinas para mejorar el rendimiento del dispositivo. Los resultados apuntan hacia una dirección importante para impulsar el rendimiento de las células solares de perovskita y otros dispositivos electrónicos al reducir la densidad de trampas en la interfaz.
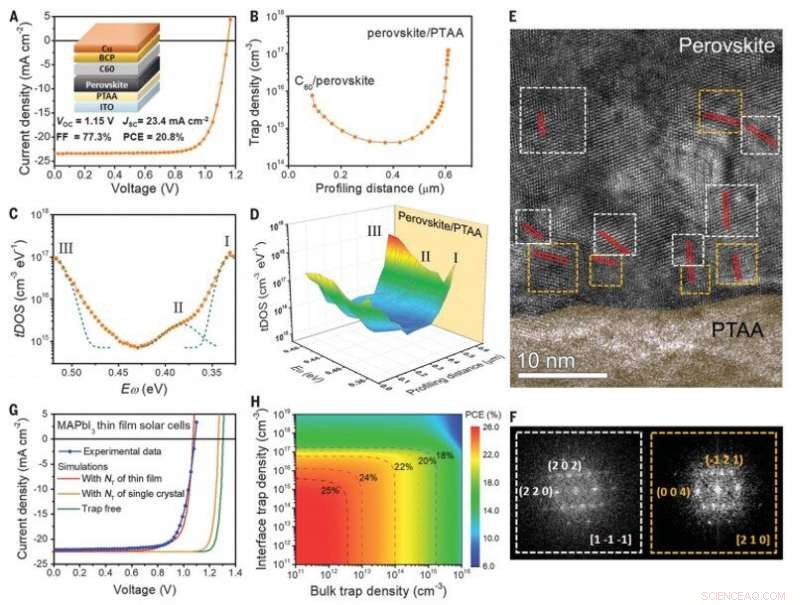
Distribuciones espacial y energética de estados trampa en películas delgadas de perovskita. (A) Curva J-V de las células solares de película delgada Cs0.05FA0.70MA0.25PbI3. El recuadro muestra la estructura del dispositivo. (B) Dependencia de la densidad de la trampa de la distancia de perfilado para la película delgada de perovskita en la celda solar medida a una frecuencia de CA de 10 kHz. (C) tDOS de la célula solar de película delgada de perovskita, medido por el método TAS. (D) Mapeo espacial y energético de las densidades de los estados de trampa de la película delgada de perovskita en la célula solar, medido por DLCP. (E) Imagen HR-TEM en sección transversal de la pila de perovskita y PTAA. Los cuadrados punteados marcan las áreas donde se realizaron las transformadas rápidas de Fourier de las celosías, con ejes de zona indicativos blancos y amarillos de [1 −1 −1] y [2 1 0], respectivamente. Las líneas rojas indican la orientación de las facetas. (F) Transformadas rápidas de Fourier de las áreas indicadas en (E). (G) Curvas J-V medidas y simuladas de células solares de estructura plana basadas en películas delgadas policristalinas MAPbI3. Para las simulaciones se adoptaron las densidades de trampa de interfase y de volumen de película delgada (monocristal). (H) Dependencia del PCE de la celda solar de película delgada MAPbI3 en las densidades de trampa de interfaz y de volumen. Las líneas discontinuas denotan las curvas de nivel de ciertos valores de PCE, que se anotan. Crédito:Ciencia, doi:10.1126 / science.aba0893
De este modo, Zhenyi Ni y sus colegas utilizaron el simulador de capacitancia de células solares para simular las células solares de perovskita de película fina y monocristal con densidades de trampa variables. El rango de trampas medidas con las mediciones de DLCP fue lo suficientemente profundo como para predecir el comportamiento de las células solares y reducir la densidad de trampas a granel de los materiales y aumentar la eficiencia de conversión de energía (PCE) hasta en un 20 por ciento. Al disminuir la densidad de trampas de la interfaz, aumentaron los valores de PCE más cerca del PCE observado para una celda solar de película delgada sin trampas. Los datos simulados para células solares monocristalinas coincidieron bien con los experimentos, mostrando que el PCE de la celda solar monocristalina podría mejorarse aún más en la interfaz del dispositivo para recolectar más luz solar.
© 2020 Science X Network