
Interacciones de ondas de solitón en aguas poco profundas. Crédito:Liron Barakiva
A veces en aguas poco profundas se puede formar un tipo de onda mucho más estable que las ondas ordinarias. Llamados solitones, Estos fenómenos emergen como ondas solitarias y pueden viajar largas distancias manteniendo su forma y velocidad. incluso después de chocar con otras olas.
Sin embargo, en ciertos casos, las colisiones de solitones pueden generar patrones de onda complicados, a veces llamadas "ondas alfabéticas", ya que se parecen a las letras X, Y, y H, así como combinaciones de estas formas. Las ondas de solitón y sus patrones de colisión han fascinado a los científicos desde que fueron descubiertos en el siglo XIX. th siglo.
Ahora en un nuevo estudio, Los investigadores han descubierto que estos mismos patrones en las ondas de agua también surgen en colisiones de solitones ópticos (ondas de luz con las mismas propiedades estables). Los investigadores muestran que la misma ecuación, llamada ecuación de Kadomtsev-Petviashvili II (KPII), que se usa para modelar interacciones de solitones de agua también se puede usar para modelar interacciones de solitones ópticos, revelando una estrecha conexión entre la dinámica de las olas del agua y la luz.
Theodoros P. Horikis, en el Departamento de Matemáticas, Universidad de Ioannina, y Dimitrios J. Frantzeskakis, en el Departamento de Física, Universidad de Atenas, han publicado un artículo sobre los patrones en solitones ópticos en un número reciente de Actas de la Royal Society A .
"Todos hemos estado en una playa y hemos notado los intrincados patrones que forman las olas en la poca profundidad, cerca de la costa:hermosa X-, Y-, e incluso las formas de onda en forma de H surgen con frecuencia de la interacción de ondas rectas, "Horikis dijo Phys.org . "Notablemente, estos fenómenos se comprenden completamente y se pueden describir matemáticamente en detalle utilizando modelos matemáticos apropiados. Tensión superficial, que es el fenómeno que hace que los fluidos minimicen el área que ocupan, juega un papel importante en la formación de X-, Y-, y ondas en forma de H. En agua, la tensión superficial es pequeña, mientras que en mercurio, por ejemplo, la tensión superficial es grande.
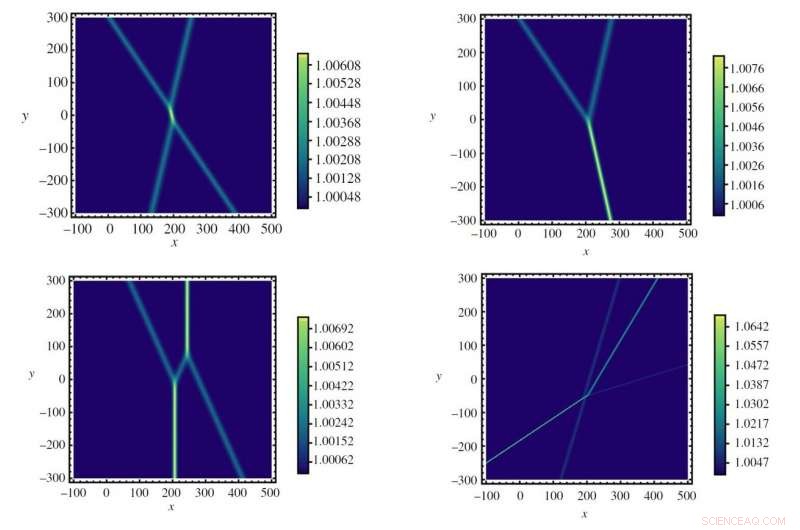
Resultados de simulación que muestran diferentes patrones emergentes en interacciones de solitones ópticos. Crédito:Horikis y Frantzeskakis. © 2019 La Real Sociedad
"Hemos demostrado que la propagación óptica de solitones en medios no locales, que incluyen plasmas, cristales líquidos nemáticos y soluciones líquidas con no linealidades térmicas:se rige por el mismo modelo que se utiliza para describir aguas poco profundas, con la no localidad desempeñando el papel de tensión superficial. Por lo tanto, Por supuesto, 'la luz se encuentra con el agua, 'ya que predecimos que X-, Y-, En forma de H, y estructuras de olas aún más complicadas que observamos en playas planas también se pueden observar en óptica, como haces ópticos que se propagan en medios no lineales no locales ".
Como explicaron los investigadores, un medio óptico no es local cuando su respuesta a la luz depende no solo de la posición donde se aplica el campo óptico externo (como en un medio local), sino también sobre la superficie total y el volumen del medio. En medios no locales, la luz que incide en un punto determinado se lleva a la región circundante, de modo que un haz óptico localizado estrecho puede inducir una respuesta espacialmente amplia del medio. La analogía entre la tensión superficial débil del agua y la no localidad fuerte en ciertos medios ópticos es lo que permite la descripción de los solitones ópticos en términos de la ecuación KPII.
"Lo importante en nuestro artículo es que estos dos fenómenos, no localidad en óptica y tensión superficial en el agua, parecen tener una correspondencia uno a uno, por así decirlo, "Horikis dijo." Es importante destacar que, solitones ópticos que serían inestables en medios con una no localidad débil, o en fluidos con fuerte tensión superficial (como el mercurio), puede volverse estable en medios ópticos fuertemente no locales. Debido a este importante efecto estabilizador inducido por la fuerte no localidad, el medio óptico anfitrión puede soportar solitones como la superficie del agua, cuyo contacto con el aire actúa como una fina lámina elástica sobre la que pueden formarse estas 'ondas alfabéticas' ".
Basado en este resultado, los investigadores utilizaron simulaciones numéricas para modelar colisiones de dos o tres solitones ópticos. Similar al caso del solitón de agua, encontraron que X-, Y-, y surgieron ondas en forma de H, y también que el ángulo de los solitones en interacción conduce a diferentes patrones.
Los investigadores esperan que sea posible observar experimentalmente estos patrones de solitones ópticos mediante el uso de tecnología recientemente utilizada para observar solitones individuales. Esto requeriría combinar dos solitones dentro de un medio no local, por ejemplo, un cristal líquido nemático, mientras se utilizan espejos para controlar el ángulo entre los dos haces de luz utilizados para generar los solitones.
Sus hallazgos sugieren que en el futuro también puede ser posible encontrar patrones aún más intrincados, como estructuras de ondas en forma de red, en colisiones de solitones ópticos. También planean investigar si otros sistemas altamente no locales, como condensados de Bose-Einstein (sistemas cuánticos macroscópicos compuestos por átomos ultrafríos) y coloides (mezclas que contienen partículas suspendidas en solución), también puede proporcionar los ingredientes necesarios para apoyar la aparición de estos patrones.
© 2019 Science X Network