
Galaxia espiral M81. Crédito:NASA / JPL-Caltech / ESA / Harvard-Smithsonian CfA
El astrónomo del siglo XVII Johannes Kepler fue el primero en reflexionar sobre la estructura de los copos de nieve. ¿Por qué son tan simétricos? ¿Cómo sabe un lado cuánto tiempo ha crecido el lado opuesto? Kepler pensó que todo se debía a lo que ahora llamaríamos un "campo morfogénico":que las cosas querer para tener la forma que tienen. Desde entonces, la ciencia ha descartado esta idea. Pero la cuestión de por qué los copos de nieve y estructuras similares son tan simétricas, no obstante, no se comprende del todo.
La ciencia moderna muestra cuán fundamental es la pregunta:observe todas las galaxias espirales que hay. Pueden tener medio millón de años luz de diámetro, pero aún conservan su simetría. ¿Cómo? En nuestro nuevo estudio, publicado en Informes científicos , presentamos una explicación.
Hemos demostrado que la información y la "entropía", una medida del desorden de un sistema, están vinculadas ("infoentropía") de una manera exactamente análoga a los campos eléctricos y magnéticos ("electromagnetismo"). Las corrientes eléctricas producen campos magnéticos, mientras que los campos magnéticos cambiantes producen corrientes eléctricas. La información y la entropía se influyen mutuamente de la misma manera.
La entropía es un concepto fundamental en física. Por ejemplo, debido a que la entropía nunca puede disminuir (el desorden siempre aumenta), puede convertir un huevo en huevos revueltos, pero no al revés. Si mueve información, también debe aumentar la entropía; una llamada telefónica tiene un costo de entropía.
Demostramos que la entropía y la información pueden tratarse como un campo y que están relacionadas con la geometría. Piense en las dos hebras de la doble hélice de ADN que se enrollan una alrededor de la otra. Las ondas de luz tienen la misma estructura, donde las dos hebras son los campos eléctrico y magnético. Demostramos matemáticamente que la relación entre la información y la entropía se puede visualizar usando la misma geometría.

Copo de nieve real. Crédito:Karen Schanely:https://www.clickinmoms.com/blog/take-macro-snowflakes-pictures/; dominio publico
Queríamos ver si nuestra teoría podía predecir cosas en el mundo real, y decidió intentar calcular cuánta energía necesitaría para convertir una forma de ADN en otra. Después de todo, el ADN es una espiral y una forma de información.
En realidad, esto se hizo con medidas extraordinariamente precisas hace unos 16 años. Los investigadores sacaron una molécula de ADN recta (al ADN le gusta acurrucarse), y lo torciste 4, 800 vueltas sujetando los extremos con unas pinzas ópticas. El ADN pasó de una forma a otra, como en la imagen de arriba. Luego, los investigadores pudieron calcular la diferencia de energía entre las dos formas.
Pero nuestra teoría podría calcular esta diferencia de energía, también. Conocíamos la entropía de cada una de las dos versiones de esta molécula de ADN, y la energía es simplemente el producto de la entropía y la temperatura. Nuestro resultado fue acertado:la teoría pareció sostenerse.
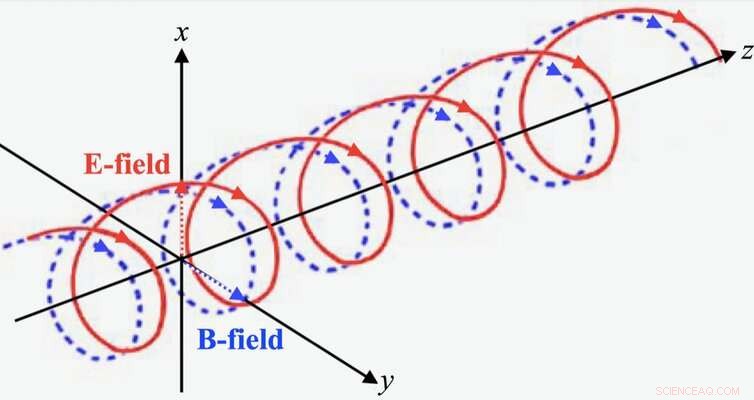
Onda de luz con campos eléctricos (E) y magnéticos (B). Autor proporcionado
De diminuto a enorme
Las galaxias espirales son espirales dobles al igual que el ADN es una hélice doble; matemáticamente hablando, tienen geometrías similares.
Nuestra teoría muestra directamente por qué los dos brazos de las galaxias espirales son simétricos, es porque los campos de infoentropía dan lugar a fuerzas (como otros campos). Las estrellas de la galaxia están simplemente coreografiadas por una fuerza entrópica para alinearse en un par de espirales para maximizar la entropía.
Pero queríamos obtener algunos números reales también. Por lo tanto, decidimos intentar calcular la masa de nuestra galaxia a partir de nuestra teoría. Sabemos lo pesada que parece ser la Vía Láctea por lo rápido que se mueven las estrellas cerca del borde galáctico:tiene aproximadamente 1,3 billones de masas solares.
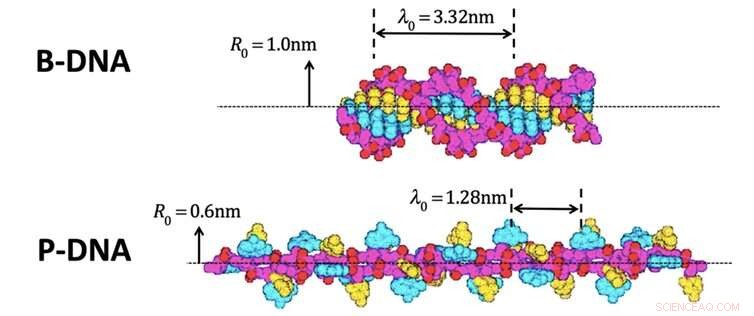
Dos formas de ADN. Crédito:Parker &Jeynes, Figura 1 de los informes científicos 9 | 10779 (2019); Modificado de la Fig. 5 de Allemand et al. Proc. Natl. Acad. Sci. Estados Unidos 95, 14152–14157 (1998), CC BY
Extrañamente, esto es en realidad mucho más que la masa de todas las estrellas visibles en la galaxia. Para poder explicar esta discrepancia y explicar por qué las estrellas se mueven mucho más rápido de lo esperado, A los astrónomos se les ocurrió la idea de la "materia oscura":masa invisible que acecha en la galaxia, aumentando su atracción gravitacional sobre las estrellas.
Necesitábamos conocer la entropía de la galaxia para nuestros cálculos. Afortunadamente, el físico matemático Roger Penrose demostró que esta entropía está dominada por la entropía de su agujero negro supermasivo central.
Conocemos la masa de este agujero negro (4,3 millones de masas solares). Y sorprendentemente cuando conoces la masa de un agujero negro, hay una ecuación, descubierto por el difunto físico Stephen Hawking, que calcula su entropía. Hawking también descubrió cómo calcular la "temperatura" en su superficie, o "horizonte de sucesos".
Si puede asignar una "temperatura" al horizonte de sucesos del agujero negro, que no tiene nada para tener temperatura, ¿por qué no asignar también una temperatura a una galaxia? Argumentamos en nuestro artículo que esto es razonable (usando lo que se conoce como el "principio holográfico"). Entonces usamos nuestras ecuaciones de info-entropía para calcular la temperatura holográfica de la galaxia.

Una galaxia espiral con una espiral logarítmica de dos brazos superpuesta. Crédito:Parker &Jeynes, Figura 2 de Informes científicos 9 | 10779 (2019), CC BY-SA
Entonces se vuelve fácil. Sabemos que la energía galáctica viene dada por el producto de su entropía y temperatura. Y cuando conocemos la energía podemos averiguar la masa gracias a la famosa ecuación de Einstein:E =mc 2 .
Esta vez el resultado no fue exactamente acertado, pero estuvo razonablemente cerca dado nuestro modelo altamente simplificado de la galaxia. La geometría info-entrópica de una galaxia no solo explica cómo las fuerzas entrópicas crean la forma bellamente simétrica y la mantienen, pero también explica toda la masa que parece ser evidente en él.
Esto significa que, después de todo, en realidad no necesitamos materia oscura. Según nuestro modelo, la entropía galáctica da lugar a una cantidad tan grande de energía adicional que modifica la dinámica observada de la galaxia, haciendo que las estrellas del borde se muevan más rápido de lo esperado. Esto es exactamente lo que pretendía explicar la materia oscura. La energía no es directamente observable como masa, pero su presencia está ciertamente respaldada por las observaciones astronómicas, lo que explica por qué las búsquedas de materia oscura hasta ahora no han encontrado nada.
Sin embargo, hay muchas investigaciones que respaldan la idea de la materia oscura. Nuestra teoría sugiere una explicación alternativa de las observaciones, y no necesita nueva física. Por supuesto, Se necesita un trabajo más detallado para verificar que la verdadera complejidad de las observaciones también se puede modelar con éxito.
Creemos que el "campo morfogénico" que Kepler buscaba realmente existe, y es en realidad el efecto del entrelazamiento de información y entropía. Después de cuatro largos siglos, parece que Kepler finalmente ha sido reivindicado.
Este artículo se ha vuelto a publicar de The Conversation con una licencia de Creative Commons. Lea el artículo original. 