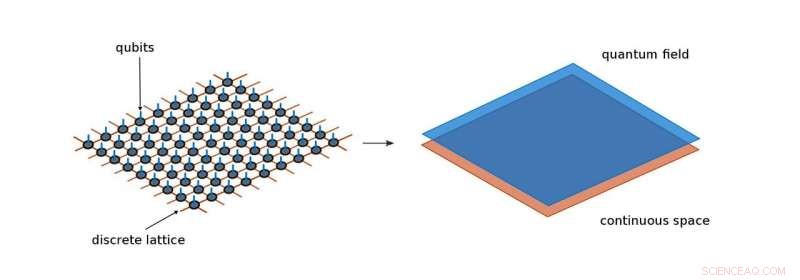
Los estados de red de tensor estándar describen sistemas cuánticos que viven en un espacio discreto, o celosía, por ejemplo, una matriz de qubits. Redes de tensores continuos, por otra parte, encoger las distancias de la celosía hasta que sean infinitamente pequeñas y así restaurar la continuidad del espacio. De esta manera, pueden tratar con campos cuánticos de forma más directa. Crédito:Instituto Max Planck de Óptica Cuántica
Calcular con precisión la dinámica de muchas partículas cuánticas que interactúan es una tarea abrumadora. Sin embargo, existe un método de cálculo prometedor para tales sistemas:redes de tensores, que se están investigando en la división de teoría del Instituto Max Planck de Óptica Cuántica. El enfoque inicial de la red tensorial estaba en partículas cuánticas restringidas a una red, tal como ocurren en los cristales, por ejemplo, o en los registros cuánticos de las futuras computadoras cuánticas. En un nuevo periódico el investigador postdoctoral Antoine Tilloy y el director de la división de teoría Ignacio Cirac lograron extender este enfoque al continuo. Un objetivo a largo plazo es un elegante método de cálculo para las teorías cuánticas de campos que describe las fuerzas básicas de la física.
Describir los sistemas en los que interactúan muchas partículas cuánticas y producen colectivamente nuevos fenómenos es uno de los desafíos fundamentales de la física. Un ejemplo de tal fenómeno cuántico de muchos cuerpos es la superconductividad. La dificultad actual es que las partículas se influyen entre sí. Como resultado, las ecuaciones de la mecánica cuántica que describen este comportamiento colectivo pueden derivarse, pero no resuelto exactamente.
En mecánica cuántica, la ecuación dinámica debe capturar todos los estados posibles en los que potencialmente puede estar el sistema. Y puede haber muchos. Un ejemplo actualmente popular en física son los bits cuánticos. Se obtienen, por ejemplo, de electrones especialmente preparados o átomos cargados eléctricamente. Tales qubits tienen dos estados opuestos, que puede tomar los valores cero y uno. Pero a diferencia de un bit "clásico", el qubit también se puede ubicar en cualquier superposición de esos dos estados. Si ahora se emparejan dos qubits con una llamada puerta cuántica, el espacio matemático abstracto de todos los estados cuánticos posibles se duplica. Y cada qubit adicional lo duplica de nuevo. Los procesadores y las memorias de datos de las computadoras convencionales están literalmente invadidos por este número cada vez mayor de posibles estados cuánticos. Incluso las supercomputadoras fallan después de más de unas pocas docenas de qubits. Solo computadoras cuánticas, obedecer las propias reglas de la mecánica cuántica, Algún día podrá lidiar con la dinámica de sistemas cuánticos más grandes.
Haciendo calculable lo incalculable
El ejemplo de los qubits encaja, porque Ignacio Cirac y sus colegas se encuentran entre los pioneros de este campo emergente de la tecnología de la información cuántica. El método de "redes tensoras, "que es el tema de este documento, también se origina en este campo de investigación. Permite reducir inteligentemente el espacio gigantesco de todos los estados cuánticos posibles de un sistema de múltiples partículas a un tamaño calculable. "Imagine todos los estados cuánticos posibles de un sistema de muchas partículas como un área circular enorme, ", explica Antoine Tilloy." Pero los estados que son realmente relevantes para nuestro sistema encajan dentro de un círculo mucho más pequeño ". El arte ahora está en encontrar este pequeño círculo en un espacio matemático abstracto, y eso es lo que pueden hacer las redes tensoras.
Tilloy es investigadora postdoctoral en el grupo de Cirac y juntos acaban de publicar un artículo sobre redes tensoras en la revista Revisión física X . Originalmente, los físicos los aplicaron a matrices de qubits individuales. Por lo tanto, las redes de tensores se basaban inicialmente en una cuadrícula de objetos matemáticos abstractos, un poco como una cadena matemática de perlas, viviendo en posiciones discretas.
Las redes de tensores demostraron ser una herramienta exitosa para realizar cálculos para una gran clase de sistema cuántico confinado a las redes. Este éxito dio una idea a los grupos de investigación teóricos de todo el mundo:¿podría este método aplicarse también a sistemas físicos que no viven en redes? sino más bien en el espacio continuo? En breve, la respuesta es sí. De hecho, el método de las redes tensoriales puede extenderse al continuo y esto es lo que demostraron Tilloy y Cirac en su nuevo trabajo.
Nueva herramienta para teorías cuánticas de campos
Las llamadas teorías cuánticas de campos podrían ser un campo de aplicación importante para esta nueva caja de herramientas. Estas teorías forman la base de la cosmovisión física actual. Describen con precisión cómo funcionan tres de las cuatro fuerzas básicas de la física según la mecánica cuántica. Estas fuerzas están mediadas por partículas virtuales que existen solo durante el corto período de tiempo necesario para transmitir su fuerza.
En la fuerza eléctrica por ejemplo, las partículas mediadoras son cuantos de luz virtuales. "Esto cae dentro de lo que se conoce como electrodinámica cuántica y se comprende bien, ", dice Tilloy." Las cosas se complican más con lo que se conoce como cromodinámica cuántica ". QCD, como se llama brevemente, describe las fuerzas entre los quarks, que a su vez forman los bloques de construcción de los núcleos atómicos, los protones y neutrones. Gluones, "partículas adhesivas, "median la fuerza más fuerte de la física. Y esto" pega "los quarks juntos.
Pero a diferencia de los fotones virtuales, los gluones también pueden influirse fuertemente entre sí. Esta "auto-interacción" lleva al desagradable hecho de que las ecuaciones de QCD solo pueden resolverse en casos límite, a muy alta energía. Para energías más bajas, el estado normal de la materia en nuestro entorno, esto no es posible. Por esta razón, Los físicos hasta ahora tienen que trabajar con soluciones aproximadas. El paso estándar aquí es dividir el continuo en una cuadrícula artificial de puntos para los cuales una computadora poderosa puede calcular soluciones aproximadas.
"Este paso de discretización es complejo, "dice Tilloy. Además, tales simplificaciones siempre tienen la desventaja de romper una simetría fundamental de la naturaleza al dividir el continuo en una cuadrícula de puntos discretos. Por lo tanto, se ven obligados a alejarse de la física real. El método de las redes de tensores continuos podría ayudar aquí, porque no requiere esta previa discretización del espacio. Quizás algún día se entienda el comportamiento de los quarks y gluones a bajas energías. Hoy sigue siendo un problema abierto, pero es posible que las redes de tensores continuos descubiertas recientemente ya sean parte de la solución.