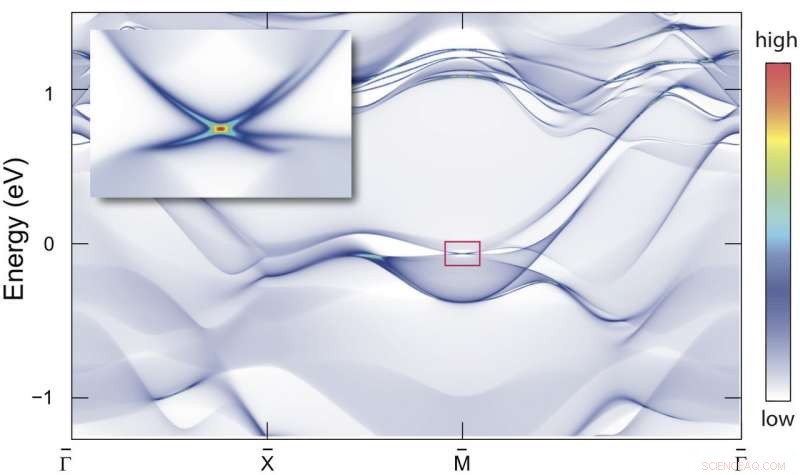
Un material aislante recientemente identificado que utiliza los principios de simetría detrás de los patrones de papel tapiz puede proporcionar una base para la computación cuántica. según un equipo internacional de investigadores. Esta muestra de estroncio-plomo (Sr2Pb3) tiene un estado de superficie de cono de Dirac cuádruple, un juego de cuatro, Estados superficiales electrónicos bidimensionales que se alejan de un punto en el espacio de momento en línea recta. Crédito:Benjamin Wieder, Departamento de Física de la Universidad de Princeton
Un equipo internacional de científicos ha descubierto un nuevo forma exótica de material aislante con una superficie metálica que podría permitir una electrónica más eficiente o incluso la computación cuántica. Los investigadores desarrollaron un nuevo método para analizar compuestos químicos existentes que se basa en propiedades matemáticas como la simetría que gobiernan los patrones repetidos que se ven en el papel tapiz cotidiano.
"La belleza de la topología es que se pueden aplicar principios de simetría para buscar y clasificar materiales, "dijo B. Andrei Bernevig, profesor de física en Princeton.
La investigación, que aparece el 20 de julio en la revista Ciencias , implicó una colaboración entre grupos de la Universidad de Princeton, la Universidad de Pensilvania (Penn), Universidad de Sungkyunkwan, Freie Universität Berlin y el Instituto Max Planck de Física de Microestructuras.
El descubrimiento de esta forma de plomo-estroncio (Sr 2 Pb 3 ) completa una búsqueda de una década de un material tridimensional elusivo que combina las propiedades electrónicas únicas del grafeno bidimensional y los aislantes topológicos tridimensionales, una fase de la materia descubierta en 2005 en obras independientes de Charles Kane en Penn y Bernevig en Princeton.
Algunos científicos han teorizado que los aislantes topológicos, que aíslan en su interior pero conducen electricidad en su superficie, podría servir como base para la computación cuántica súper rápida.
"Puedes pensar en un aislante topológico como el beso de Hershey, "dijo Kane, un autor correspondiente en el artículo. “El chocolate es el aislante y la lámina es un conductor. Hemos estado tratando de identificar nuevas clases de materiales en los que las simetrías cristalinas protegen la superficie conductora. Lo que hemos hecho aquí es identificar el tipo más simple de aislante cristalino topológico. "
El nuevo trabajo demuestra cómo las simetrías de ciertas superficies bidimensionales, conocidos como los 17 grupos de papel tapiz por su patrón similar al papel tapiz, Restringir la disposición espacial (topología) de los aisladores tridimensionales.
En un aislante topológico tridimensional convencional, cada superficie bidimensional exhibe un único grupo característico de estados con dispersión en forma de cono. Estos conos se asemejan a los elementos del grafeno llamados conos de Dirac, características que imbuyen el material y otros semimetales bidimensionales de Dirac con sus inusuales cualidades de transporte electrónico, pero son distintos porque el grafeno posee un total de cuatro conos de Dirac en dos pares que están "pegados" entre sí.
Kane había sospechado que con simetrías de cristal, podría existir un segundo tipo de aislante topológico con un solo par de conos de Dirac pegados. "Me di cuenta de que un solo par de conos de Dirac es imposible en un material puramente bidimensional, pero podría ser posible en la superficie de un nuevo tipo de aislante topológico. Pero cuando traté de construir tal estado, los dos conos siempre se despegaban ".
Una solución surgió cuando Benjamin Wieder, luego un estudiante de posgrado en el grupo de Kane y ahora un asociado postdoctoral de Princeton, visitó Princeton. En Princeton, Bernevig y su colega Zhi Jun Wang acababan de descubrir "aislantes de reloj de arena", aislantes topológicos con patrones extraños de estados entrelazados similares a relojes de arena, que Wieder reconoció que actuaban como si se hubiera envuelto un cristal tridimensional con un tipo especial de papel tapiz estampado.
"Nos dimos cuenta de que no solo se podía conseguir el aislante de reloj de arena, pero también este aislante especial de Dirac, al encontrar un cristal que parecía estar cubierto con el papel tapiz correcto, "dijo Wieder.
En particular, reconocieron que un par de conos de Dirac pegados podría estabilizarse en superficies de cristal que tienen dos líneas que se cruzan a lo largo de las cuales las superficies se ven idénticas después de voltearlas y girarlas perpendicularmente. Estas líneas, conocidos como reflejos de deslizamiento, caracterizar los denominados grupos de papel tapiz no simmórficos, y así dar nombre a esta nueva fase, que el equipo denominó "aislante de Dirac no simmórfico".
Los investigadores rápidamente se pusieron a trabajar aplicando el rigor matemático a la inspiración de Wieder, resultando en un nuevo, metodología basada en la simetría del papel tapiz para diagnosticar la topología global de cristales tridimensionales.
"Los principios básicos son tan simples que los dibujamos en servilletas esa misma noche, "dijo el coautor Barry Bradlyn, investigador asociado en el Centro de Ciencias Teóricas de Princeton (PCTS).
"Sin embargo, son lo suficientemente robustos como para predecir y comprender un zoológico de nuevas fases topológicas en materiales reales, "dijo Wang, un asociado de investigación postdoctoral en física.
El descubrimiento permitió a los científicos relacionar directamente la simetría de una superficie con la presencia de los estados de superficie topológicos deseados por primera vez. dijo Andrew Rappe de Penn, otro coautor del artículo. "Esto permite un medio elegante e inmediatamente útil para diseñar superficies deseables y estados de interfaz".
Para identificar la fase aislante de Dirac en la naturaleza, los investigadores calcularon las estructuras electrónicas de cientos de compuestos previamente sintetizados con superficies con dos líneas de deslizamiento (grupos de papel tapiz pgg y p4g) antes de identificar la nueva topología en plomo-estroncio.
Los químicos computacionales "sabían que estaban buscando una aguja en un pajar, pero nadie se molestó en decirles lo pequeña que podría ser la aguja, "dijo Jennifer Cano, investigador asociado en PCTS.
A medida que se descubren aisladores topológicos aún más exóticos, el papel de la simetría del grupo de papel tapiz, y de lo especial, conos de grafeno en el aislante de Dirac, se han solidificado aún más.
"Cuando se puede dividir un cono de Dirac de superficie real mientras se mantiene la simetría de inversión del tiempo, sucede algo realmente especial, "Se obtienen aislantes tridimensionales cuyas superficies bidimensionales también son una especie de aislante topológico", dijo Bernevig. Varios miembros de la colaboración han predicho recientemente estas fases en cristales de bismuto y ditelurida de molibdeno (MoTe2).
Es más, con el uso de una nueva teoría, química cuántica topológica, los investigadores esperan encontrar muchas más de estas fases exóticas.
"Si pudiéramos pintar estos materiales con el papel pintado adecuado, veríamos más aisladores Dirac, "dijo Wieder, "pero a veces, el fondo de pantalla incorrecto también es interesante ".