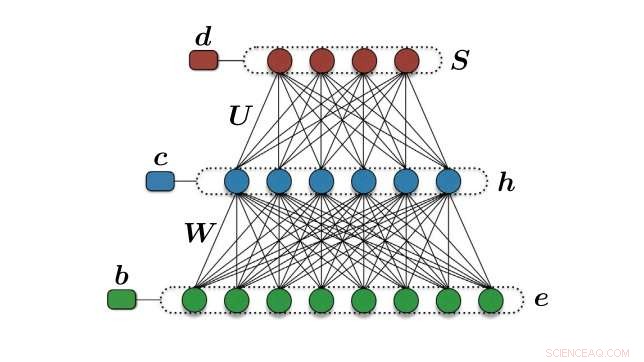
La arquitectura del decodificador neuronal. Crédito:Torlai et al. © 2017 Sociedad Estadounidense de Física
(Phys.org) —Los físicos han aplicado la capacidad de los algoritmos de aprendizaje automático para aprender de la experiencia a uno de los mayores desafíos que enfrenta actualmente la computación cuántica:la corrección de errores cuánticos, que se utiliza para diseñar protocolos de computación cuántica tolerantes al ruido. En un nuevo estudio, han demostrado que se puede entrenar un tipo de red neuronal llamada máquina de Boltzmann para modelar los errores en un protocolo de computación cuántica y luego diseñar e implementar el mejor método para corregir los errores.
Los físicos Giacomo Torlai y Roger G. Melko en la Universidad de Waterloo y el Instituto Perimetral de Física Teórica, han publicado un artículo sobre el nuevo algoritmo de aprendizaje automático en un número reciente de Cartas de revisión física .
"La idea detrás de la decodificación neuronal es eludir el proceso de construcción de un algoritmo de decodificación para la realización de un código específico (dadas algunas aproximaciones sobre el ruido), y deje que una red neuronal aprenda a realizar la recuperación directamente a partir de datos sin procesar, obtenido por simples mediciones en el código, "Torlai dijo Phys.org . "Con los recientes avances en tecnologías cuánticas y una ola de dispositivos cuánticos que estarán disponibles en el corto plazo, Los decodificadores neuronales podrán adaptarse a las diferentes arquitecturas, así como diferentes fuentes de ruido ".
Como explican los investigadores, una máquina de Boltzmann es uno de los tipos más simples de redes neuronales artificiales estocásticas, y se puede utilizar para analizar una amplia variedad de datos. Las redes neuronales suelen extraer características y patrones de datos sin procesar, que en este caso es un conjunto de datos que contiene los posibles errores que pueden afectar a los estados cuánticos.
Una vez que el nuevo algoritmo, que los físicos llaman decodificador neuronal, está capacitado en estos datos, es capaz de construir un modelo preciso de la distribución de probabilidad de los errores. Con esta información, el decodificador neuronal puede generar las cadenas de error apropiadas que luego pueden usarse para recuperar los estados cuánticos correctos.
Los investigadores probaron el decodificador neuronal en códigos topológicos cuánticos que se utilizan comúnmente en la computación cuántica. y demostró que el algoritmo es relativamente sencillo de implementar. Otra ventaja del nuevo algoritmo es que no depende de la geometría específica, estructura, o dimensión de los datos, lo que permite generalizarlo a una amplia variedad de problemas.
En el futuro, los físicos planean explorar diferentes formas de mejorar el rendimiento del algoritmo, por ejemplo, apilando varias máquinas Boltzmann una encima de la otra para construir una red con una estructura más profunda. Los investigadores también planean aplicar el decodificador neuronal a más complejos, códigos realistas.
"Hasta aquí, Los decodificadores neuronales se han probado en códigos simples que se utilizan normalmente para evaluaciones comparativas, "Torlai dijo." Una primera dirección sería realizar la corrección de errores en los códigos para los que aún no se ha encontrado un decodificador eficiente, por ejemplo, códigos de verificación de paridad de baja densidad. A largo plazo, creo que la decodificación neuronal desempeñará un papel importante cuando se trate de sistemas cuánticos más grandes (cientos de qubits). La capacidad de comprimir objetos de alta dimensión en representaciones de baja dimensión, de donde proviene el éxito del aprendizaje automático, permitirá captar fielmente la compleja distribución relacionando los errores que surgen en el sistema con los resultados de las mediciones ".
© 2017 Phys.org