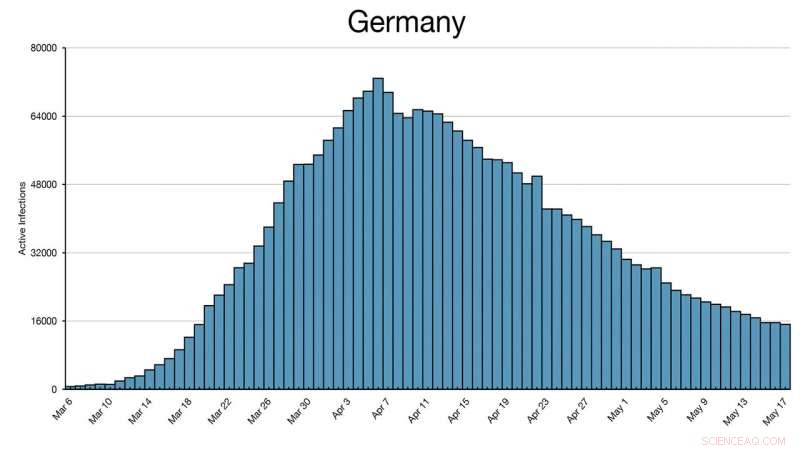
Este histograma de Alemania muestra que alcanzó su punto máximo el 6/4/20 y reabrió parcialmente en abril. La frontera con Austria permaneció cerrada a excepción de los desplazamientos laborales. Las fronteras se reabrieron el 15/6/20, pero en las empresas alemanas se usaron máscaras hasta julio. Alemania no decayó al nivel del 16/3/20 hasta el 10/6/20, casi tres meses después. Crédito:Joseph Lee McCauley
Durante los primeros meses de la pandemia COVID-19, Joseph Lee McCauley, profesor de física en la Universidad de Houston, estaba observando los datos diarios de seis países y se preguntaba si las infecciones realmente estaban creciendo exponencialmente. Extrayendo los tiempos de duplicación de los datos, se convenció de que lo eran.
Los tiempos de duplicación y el crecimiento exponencial van de la mano, por lo que le quedó claro que el modelado basado en infecciones pasadas es imposible, porque la tasa cambia imprevisiblemente de un día a otro debido al distanciamiento social y los esfuerzos de bloqueo. Y los cambios en las tasas difieren para cada país en función del grado de distanciamiento social.
En Anticipos de AIP , McCauley explica cómo combinó las matemáticas en la forma de la desigualdad de Tchebychev con un conjunto estadístico para comprender cómo el crecimiento exponencial macroscópico con diferentes tasas diarias surge de la infección de una enfermedad de persona a persona.
"Ecuaciones cinéticas químicas ordinarias discretizadas aplicadas a infectados, no infectado, y partes recuperadas de la población me permitieron organizar los datos, para poder separar los efectos del distanciamiento social y las recuperaciones dentro de las tasas diarias de infección, "Dijo McCauley.
Se produce una meseta sin pico si la tasa de recuperación es demasiado baja, y los EE. UU., REINO UNIDO., y Suecia entran en esa categoría. Las ecuaciones no se pueden iterar para mirar hacia el futuro, porque se desconoce la tasa de mañana hasta que se desarrolle.
"Los modeladores tienden a aplicar incorrectamente las ecuaciones cinéticas químicas como SIR (Susceptible, Infeccioso, o Recuperado) o SEIR (Susceptible, Expuesto, Infeccioso, o Recuperado) modelos, porque están tratando de generar tarifas futuras a partir de tarifas pasadas, ", Dijo McCauley." Pero el pasado no te permite usar ecuaciones para predecir el futuro en una pandemia, porque el distanciamiento social cambia las tarifas a diario ".
McCauley descubrió que podía hacer un pronóstico en cinco segundos a través de una calculadora manual que es tan bueno como cualquier modelo de computadora simplemente usando las tasas de infección de hoy y ayer.
"Trabajos de encierros y distanciamiento social, ", dijo McCauley." Compare Austria, Alemania, Taiwán Dinamarca, Finlandia, y varios otros países que alcanzaron su punto máximo a principios de abril, con los EE. UU., REINO UNIDO., Suecia, y otros sin encierros o encierros a medias, nunca se estancaron, mucho menos puntiagudo ".
Él enfatiza que los pronósticos no pueden prever un pico o incluso una meseta. Meseta no implica pico, y si se produce un pico, no hay nada en los datos que muestre cuándo sucederá. Ocurre cuando la tasa de recuperación es mayor que la tasa de nuevas infecciones.
"El distanciamiento social y los bloqueos reducen la tasa de infección, pero no pueden causar picos, McCauley dijo. "El distanciamiento social y las recuperaciones son dos términos separados dentro de las ecuaciones de la tasa cinética diaria".
La implicación de este trabajo es que el dinero de la investigación podría gastarse mejor que en modelos de epidemia costosos.
"Los políticos deben saber suficiente aritmética para recibir instrucciones sobre las implicaciones, "McCauley dijo." El efecto de los cierres y el distanciamiento social se manifiestan en los tiempos de duplicación observados, y también hay un tiempo de duplicación previsto basado en dos días, lo que sirve como un buen pronóstico del futuro ".