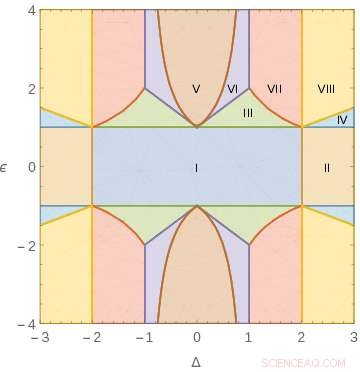
Regiones de parámetros con diferente comportamiento del límite clásico para un hamiltoniano de tipo XXZ con dos parámetros. Crédito:ICFO
Las correlaciones clásicas son parte de nuestra vida diaria. Por ejemplo, si siempre se pone un par de calcetines del mismo color y forma, mirar el color o la forma de un calcetín determina el color o la forma de su par. Aún más, observando el color y la forma de un calcetín y podemos conocer simultáneamente el color y la forma del otro.
En el reino cuántico El principio de incertidumbre de Heisenberg establece que medir con precisión un par de propiedades de un átomo pone un límite a la precisión de la medición que se puede obtener en las mismas propiedades de otro átomo. Por lo tanto, si se dice que los calcetines están enredados, observar el color de un calcetín nos permitiría predecir el color del otro. Sin embargo, si también observamos la forma del calcetín, esto "perturbaría" el color, haciéndolo completamente impredecible hasta cierto punto. Esta extraña "sincronización" entre partículas se define como entrelazamiento cuántico, y es una de las características intrínsecas del mundo cuántico.
En naturaleza, existe una forma mucho más extraña de las llamadas correlaciones no locales, que se manifiestan por algunos estados entrelazados entre partículas atómicas. Al hacer las suposiciones mínimas de que las propiedades de los objetos (forma / color) existen independientemente de nuestro conocimiento de ellas, y esa información no se puede propagar instantáneamente, uno encuentra que la física cuántica puede generar correlaciones que son incompatibles con estos dos principios aparentemente razonables.
Aunque es extremadamente fascinante de estudiar, estas correlaciones no locales son muy difíciles de caracterizar en sistemas compuestos por muchas partículas por tres razones. Primero, las correlaciones clásicas son matemáticamente muy complejas de estudiar; segundo, los estados cuánticos de muchos cuerpos son muy complejos de describir debido al crecimiento exponencial de sus estados descritos; y, tercera, Las técnicas experimentales actualmente disponibles son bastante limitadas, restringiendo las mediciones que se pueden realizar en el laboratorio. Para explorar el papel de las correlaciones no locales en los sistemas cuánticos de muchos cuerpos, por tanto, hay que abordar estos tres problemas al mismo tiempo.
En un artículo reciente publicado en Revisión física X , un equipo de científicos del MPQ en Munich, ICFO en Barcelona, La Universidad de Innsbruck y el Centro de Física Teórica de la Academia de Ciencias de Polonia han propuesto una prueba sencilla para estudiar las correlaciones no locales en sistemas cuánticos de muchos cuerpos. Han estudiado si las correlaciones no locales aparecen en sistemas naturales como estados fundamentales de algunos hamiltonianos de espín, como los electrones (descritos por su grado de libertad de giro) en un sistema de una dimensión espacial. Combinando resultados numéricos y analíticos, han demostrado que algunos hamiltonianos que han sido estudiados por físicos durante algunas décadas tienen un estado de energía mínima que puede mostrar correlaciones no locales.
Como primer autor, Jordi Tura, ha comentado, "Proporcionamos un conjunto de herramientas para estudiar un problema que siempre ha sido complicado por sí solo. Las técnicas que desarrollamos son mucho más simples que las anteriores. Si desea implementarlas en el laboratorio, sólo necesita asegurarse de que el sistema esté preparado en un estado de energía suficientemente baja ".
Los resultados arrojan algo de luz sobre este fascinante problema, Es de esperar que provoquen un mayor progreso en nuestra comprensión de la no localidad en los sistemas cuánticos de muchos cuerpos.