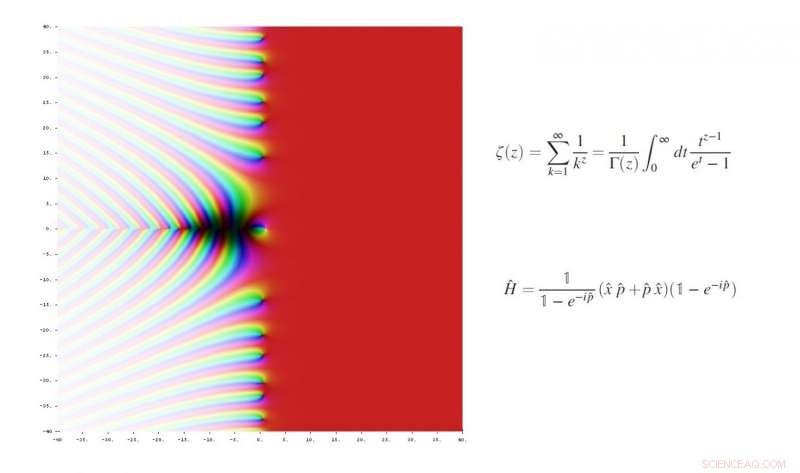
En 1859, Riemann planteó la hipótesis de que los ceros no triviales de la función zeta de Riemann se encuentran en la línea vertical (½ + it) en el plano complejo, en el que la parte real es siempre ½. Crédito:Jan Homann, Wikimedia Commons. Arriba:función zeta de Riemann. Abajo:la nueva función de operador.
(Phys.org) —Los investigadores han descubierto que las soluciones de una famosa función matemática llamada función zeta de Riemann corresponden a las soluciones de otra, diferente tipo de función que puede facilitar la resolución de uno de los mayores problemas de las matemáticas:la hipótesis de Riemann. Si los resultados pueden verificarse rigurosamente, entonces finalmente probaría la hipótesis de Riemann, que vale $ 1, 000, 000 Premio Millennium del Clay Mathematics Institute.
Si bien la hipótesis de Riemann se remonta a 1859, Durante los últimos 100 años aproximadamente, los matemáticos han estado tratando de encontrar una función de operador como la que se descubrió aquí, ya que se considera un paso clave en la prueba.
"Hasta donde sabemos, esta es la primera vez que se identifica un operador explícito, y quizás sorprendentemente relativamente simple, cuyos valores propios ['soluciones' en terminología matricial] corresponden exactamente a los ceros no triviales de la función zeta de Riemann, "Dorje Brody, físico matemático de la Universidad Brunel de Londres y coautor del nuevo estudio, dicho Phys.org .
Lo que aún queda por probar es el segundo paso clave:que todos los valores propios son números reales en lugar de imaginarios. Si el trabajo futuro puede probar esto, entonces finalmente probaría la hipótesis de Riemann.
Brody y sus coautores, los físicos matemáticos Carl Bender de la Universidad de Washington en St. Louis y Markus Müller de la Universidad de Western Ontario, han publicado su trabajo en un número reciente de Cartas de revisión física .
Espaciado de primos
La hipótesis de Riemann tiene un atractivo tan fuerte porque está profundamente conectada con la teoría de números y, en particular, los números primos. En su artículo de 1859, El matemático alemán Bernhard Riemann investigó la distribución de los números primos, o más precisamente, el problema "dado un número entero N, ¿cuántos números primos hay que son más pequeños que N? "
Riemann conjeturó que la distribución de los números primos menores que N está relacionada con los ceros no triviales de lo que ahora se llama función zeta de Riemann, ζ ( s ). (Los ceros son las soluciones, o los valores de s que hacen que la función sea igual a cero. Aunque fue fácil para los matemáticos ver que hay ceros siempre que s es un número par negativo, estos ceros se consideran ceros triviales y no son la parte interesante de la función).
La hipótesis de Riemann era que todos los ceros no triviales se encuentran a lo largo de una sola línea vertical (½ + eso ) en el plano complejo, lo que significa que su componente real es siempre ½, mientras que su componente imaginario I varía a medida que avanza y avanza en la línea.
Durante los últimos 150 años, matemáticos han encontrado literalmente billones de ceros no triviales, y todos tienen un componente real de ½, tal como pensaba Riemann. Se cree ampliamente que la hipótesis de Riemann es cierta, y se ha trabajado mucho sobre la base de esta suposición. Pero a pesar de los intensos esfuerzos, la hipótesis de Riemann —que todos los infinitos ceros se encuentran en esta única línea— aún no ha sido probada.
Soluciones idénticas
Una de las pistas más útiles para probar la hipótesis de Riemann proviene de la teoría de funciones, que revela que los valores de la parte imaginaria, t , en el que la función desaparece son números discretos. Esto sugiere que los ceros no triviales forman un conjunto de números reales y discretos, que es como los valores propios de otra función llamada operador diferencial, que es ampliamente utilizado en física.
A principios de 1900, esta similitud llevó a algunos matemáticos a preguntarse si realmente existe un operador diferencial cuyos valores propios corresponden exactamente a los ceros no triviales de la función zeta de Riemann. Hoy esta idea se llama la conjetura de Hilbert-Pólya, lleva el nombre de David Hilbert y George Pólya, a pesar de que ninguno de ellos publicó nada al respecto.
"Como no hay ninguna publicación de Hilbert o Pólya, la declaración exacta del programa Hilbert-Pólya está sujeta hasta cierto punto a interpretación, pero probablemente no sea descabellado decir que consta de dos pasos:(a) encontrar un operador cuyos valores propios correspondan a los ceros no triviales de la función zeta de Riemann; y (b) determinar si los valores propios son reales, "Dijo Brody.
"El enfoque principal de nuestro trabajo hasta ahora ha estado en el paso (a), ", dijo." Hemos identificado un operador cuyos valores propios corresponden exactamente a los ceros no triviales de la función zeta de Riemann. Solo estamos comenzando a pensar en el paso (b), y, de hecho, cómo abordar este desafío. Si será difícil o fácil completar los pasos faltantes hacia el paso (b), en este punto no podemos especular; se necesita más trabajo para tener una mejor idea de la escala de dificultad involucrada ".
El operador
Una de las cosas interesantes del operador recién descubierto es que tiene estrechos vínculos con la física cuántica.
En 1999, cuando los físicos matemáticos Michael Berry y Jonathan Keating estaban investigando la conjetura de Hilbert-Pólya, hicieron otra conjetura importante. Si tal operador existe, ellos dijeron, entonces debería corresponder a un sistema cuántico teórico con propiedades particulares. Esto ahora se llama la conjetura de Berry-Keating. Pero nadie ha encontrado un sistema así antes de ahora, y este es un segundo aspecto importante del nuevo trabajo.
"Hemos identificado una condición de cuantificación para el hamiltoniano de Berry-Keating, esencialmente verificando la validez de la conjetura de Berry-Keating, "Dijo Brody.
Los hamiltonianos se utilizan a menudo para describir la energía de los sistemas físicos. El nuevo operador, sin embargo, no parece describir ningún sistema físico, sino que es una función puramente matemática.
"Puede ser decepcionante, pero tal hamiltoniano no parece representar los sistemas físicos de ninguna manera obvia; o al menos hasta ahora no encontramos ninguna indicación de que nuestro hamiltoniano corresponda a algún sistema físico, "Dijo Brody.
"Pero uno podría preguntarse '¿por qué publicar en PRL ? ' La respuesta es porque muchas de las técnicas utilizadas para algunos análisis heurísticos en nuestro artículo que son sugestivas se toman prestadas de técnicas de la teoría cuántica pseudo-hermitiana PT-simétrica desarrolladas durante los últimos 15 años aproximadamente. La comprensión convencional de la conjetura de Hilbert-Pólya es que el operador (hamiltoniano) debería ser hermitiano, y uno naturalmente relaciona esto con la teoría cuántica por la cual se exige convencionalmente a los hamiltonianos que sean hermitianos. Proponemos una forma pseudo-hermitiana del programa Hilbert-Pólya, que nos parece que vale la pena explorar más a fondo ".
Soluciones reales
Ahora, el mayor desafío que queda es demostrar que los valores propios del operador son números reales.
En general, los investigadores son optimistas de que los valores propios son realmente reales, y en su artículo presentan un fuerte argumento a favor de esto basado en la simetría PT, un concepto de la física cuántica. Básicamente, La simetría PT dice que puede cambiar los signos de los cuatro componentes del espacio-tiempo (tres dimensiones de espacio o "paridad" y una dimensión de tiempo), y, si el sistema es PT simétrico, entonces el resultado tendrá el mismo aspecto que el original.
Aunque la naturaleza en general no es simétrica al PT, el operador que construyeron los físicos es. Pero ahora los investigadores quieren demostrar que esta simetría se rompe. Como explican en su artículo, si se puede demostrar que la simetría PT está rota para la parte imaginaria del operador, entonces se seguiría que los valores propios son todos números reales, que finalmente constituiría la tan esperada prueba de la hipótesis de Riemann.
Generalmente se considera que una prueba de la hipótesis de Riemann será muy útil en informática, especialmente criptografía. Los investigadores también quieren determinar qué podrían significar sus resultados para comprender los principios matemáticos más fundamentales.
"Lo que hemos explorado hasta ahora contiene pocos conocimientos de la teoría de los números; mientras que uno podría esperar que, dada su importancia en la teoría de números, Sin duda, cualquier intento que progrese con éxito en el establecimiento de la hipótesis de Riemann ofrecería conocimientos de la teoría de los números, "Brody dijo." Por supuesto, este no tiene por qué ser el caso en absoluto, sin embargo, sería interesante explorar si alguno de los aspectos dinámicos del sistema hipotético descrito por nuestro hamiltoniano podría estar relacionado con ciertos resultados de la teoría de números. A este respecto, El análisis semiclásico de nuestro hamiltoniano sería uno de los próximos objetivos ".
© 2017 Phys.org