Si has estado siguiendo la cobertura de Sciencing March Madness, sabes que las estadísticas y los números juegan un papel muy importante en el Torneo de la NCAA.

¿La mejor parte? No tiene que ser un fanático de los deportes para trabajar en algunos problemas matemáticos centrados en los deportes.

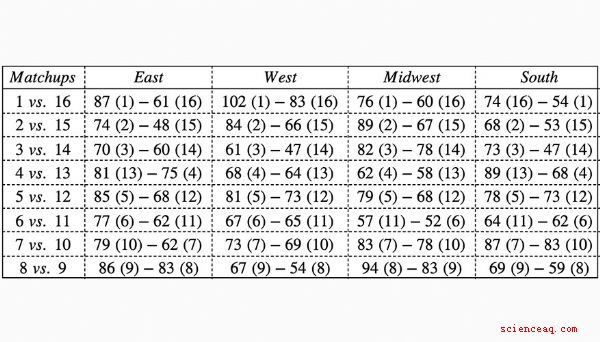
Hemos creado una serie de preguntas de matemáticas que incorporan datos de los resultados de March Madness del año pasado. La siguiente tabla muestra los resultados de cada ronda de 64 enfrentamientos de siembra. Úselo para responder las preguntas 1 a 5.

Si no desea ver las respuestas, regrese a la hoja original.

¡Buena suerte!
Preguntas sobre estadísticas:

Consulte nuestros artículos sobre la media, la mediana, la moda y el rango intercuartil si necesita repasar antes de comenzar.

Pregunta 1: ¿Cuál es la diferencia media de puntajes en Región Este, Oeste, Medio Oeste y Sur para la ronda de 64 de marzo de Madness 2018 de 2018?

Pregunta 2: ¿Cuál es la diferencia mediana de puntajes en la región Este, Oeste, Medio Oeste y Sur de 2018 para la ronda de 64 de marzo de Madness de 2018? >

Pregunta 3: ¿Cuál es el IQR (Rango Intercuartil) de diferencia de puntajes en la Región Este, Oeste, Medio Oeste y Sur para la Ronda de Locura de Marzo 2018 de 64?

Pregunta 4: ¿Qué enfrentamientos fueron atípicos en términos de la diferencia de puntajes?

Pregunta 5: ¿Qué región fue más "competitiva" en la ronda de 64 de marzo de 64 de marzo de 2018? ¿Qué métrica usarías para responder esta pregunta: media o mediana? ¿Por qué?

Competitividad:
Cuanto menor es la diferencia entre ganar y perder, más "competitivo" es el juego. Por ejemplo: si los puntajes finales de dos juegos fueron 80-70 y 65-60, entonces, según nuestra definición, el último juego fue más "competitivo".
Respuestas estadísticas:

Pregunta 1 ( diferencia de puntajes):

Este: 26, 26, 10, 6, 17, 15, 17, 3
Oeste: 19, 18, 14, 4, 8, 2, 4, 13
Medio oeste: 16, 22, 4, 4, 11, 5, 5, 11
Sur: 20, 15, 26, 21, 5, 2, 4, 10

Pregunta 2 (media de diferencia de puntajes):

Media \u003d Suma de todas las observaciones /Número de observaciones
Este: (26 + 26 + 10 + 6 + 17 + 15 + 17 + 3 ) /8 \u003d 15
Oeste: (19 + 18 + 14 + 4 + 8 + 2 + 4 + 13) /8 \u003d 10.25
Medio oeste: (16 + 22 + 4 + 4 + 11 + 5 + 5 +11) /8 \u003d 9.75
Sur: (20 + 15 + 26 + 21 + 5 + 2 + 4 + 10) /8 \u003d 12.875

Pregunta 2 (mediana de la diferencia de puntajes ):

La mediana es el valor del percentil 50.

La mediana de una lista se puede encontrar organizando los números en orden creciente y luego seleccionando el valor medio. Aquí, dado que el número de valores es un número par (8), entonces la mediana será la media de los dos valores medios, en este caso la media del 4º y 5º valor.

Este: media de 15 y 17 \u003d 16
Oeste: media de 8 y 13 \u003d 10.5
Medio oeste: media de 5 y 11 \u003d 8
sur: media de 10 y 15 \u003d 12.5

Pregunta 3 (RIC) de diferencia de puntajes):

IQR se define como la diferencia entre el percentil 75 (Q3) y el valor del percentil 25 (Q1).
\\ def \\ arraystretch {1.3} \\ begin {array} {|

c: c: c: c |

} \\ hline Region &Q1 &Q3 &IQR \\; (Q3-Q1) \\\\ \\ hline East &9 &19.25 &10.12 \\\\ \\ hdashline West &4 &15 &11 \\\\ \\ hdashline Midwest &4.75 &12.25 &7.5 \\\\ \\ hdashline South &4.75 &20.25 &15.5 \\\\ \\ hdashline \\ end {array}

Pregunta 4 (enfrentamientos atípicos):

Outliers: cualquier valor que sea menor que Q1 - 1.5 x IQR o mayor que Q3 + 1.5 x IQR
\\ def \\ arraystretch {1.3} \\ begin {array} {|

c: c: c |

} \\ hline Region &Q1-1.5 \\ times IQR &Q3 + 1.5 \\ times IQR \\\\ \\ hline East &-6.375 &34.625 \\\\ \\ hdashline West &-12.5 &31.5 \\\\ \\ hdashline Midwest &-6.5 &23. 5 \\\\ \\ hdashline South &-18.5 &43.5 \\\\ \\ hline \\ end {array}

No, valores atípicos en los datos.

Pregunta 5 (región más competitiva)
:

Orden de competitividad usando la media: Medio Oeste> Oeste> Sur> Este
Orden de competitividad usando la mediana: Medio Oeste> Oeste> Sur> Este

Dado que en este caso particular no hay valores atípicos o trabajos métricos. Pero los estudiantes deben hablar sobre el efecto de los valores atípicos en la media de las observaciones.
Preguntas de probabilidad

Consulte nuestro artículo sobre probabilidad binomial si necesita un repaso.

Tiro libre: en el baloncesto, los tiros libres o los tiros libres son intentos sin oposición de ganar puntos disparando desde detrás de la línea de tiro libre.

Suponiendo que cada tiro libre es un evento independiente, entonces calcular el éxito en el tiro libre puede ser modelado por la distribución de probabilidad binomial. Aquí están los datos de tiros libres realizados por jugadores en el juego del Campeonato Nacional 2018 y su probabilidad de golpear el tiro libre para la temporada 2017-18 (tenga en cuenta que los números se han redondeado al número decimal más cercano en un lugar).
•• • Sciencing

Pregunta 1: Calcule la probabilidad de que cada jugador obtenga el número dado de tiros libres exitosos en el número de intentos que realizó.

Respuesta:

Distribución de probabilidad binomial:
{{N} \\ elegir {k}} \\ cdot p ^ k (1-p) ^ {Nk}

Aquí hay un vistazo a la respuesta en una tabla:
\\ def \\ arraystretch {1.3} \\ begin {matriz} {|

c: c |

} \\ hline \\ bold {Jugadores} &\\ bold {Probabilidad} \\\\ \\ hline Moritz \\; Wagner &0.41 \\\\ \\ hdashline Charles \\; Matthews &0.0256 \\\\ \\ hdashline Zavier \\; Simpson &0.375 \\\\ \\ hdashline Muhammad- Ali \\; Abdur-Rahkman &0.393 \\\\ \\ hdashline Jordan \\; Poole &0.8 \\\\ \\ hdashline Eric \\; Paschall &0.32 \\\\ \\ hdashline Omari \\; Spellman &0.49 \\\\ \\ hdashline Mikal \\; Bridgers &0.64 \\\\ \\ hdashline Collin \\; Gillespie &0.41 \\\\ \\ hdashline Donte \\; DiVincenzo &0.2 \\ end {array}

Pregunta 2: Aquí están los datos de secuencia para los tiros libres de los jugadores en el mismo juego. 1 significa que el tiro libre fue exitoso y 0 significa que no fue exitoso.
••• Sciencing

Calcule la probabilidad de que cada jugador golpee la secuencia exacta anterior. ¿Es la probabilidad diferente de lo que se calculó antes? ¿Por qué?

Respuesta:
\\ def \\ arraystretch {1.3} \\ begin {array} {|

c: c |

} \\ hline \\ bold {Jugadores} &\\ bold {Probabilidad} \\\\ \\ hline Moritz \\; Wagner &0.64 \\\\ \\ hdashline Charles \\; Matthews &0.0256 \\\\ \\ hdashline Zavier \\; Simpson &0.125 \\\\ \\ hdashline Muhammad- Ali \\; Abdur-Rahkman &0.066 \\\\ \\ hdashline Jordan \\; Poole &0.8 \\\\ \\ hdashline Eric \\; Paschall &0.16 \\\\ \\ hdashline Omari \\; Spellman &0.49 \\\\ \\ hdashline Mikal \\; Bridgers &0.64 \\\\ \\ hdashline Collin \\; Gillespie &0.41 \\\\ \\ hdashline Donte \\; DiVincenzo &0.001 \\\\ \\ hline \\ end {array}

Las probabilidades pueden ser diferentes ya que en la pregunta anterior no nos importaba el orden en que "the free throws were made.", 3, [[Pero la probabilidad será la misma para los casos en los que solo hay un pedido posible. Por ejemplo:

Charles Matthews no pudo anotar un tiro libre en los 4 intentos y Collin Gillespie tuvo éxito en los 4 intentos.
Pregunta de bonificación

Usando los números de probabilidad anteriores, responda estas preguntas:

1. ¿Qué jugadores tuvieron un día desafortunado /malo con sus tiros libres?
   
2. ¿Qué jugadores tuvieron un día afortunado /bueno con sus tiros libres?
   
   

   Respuesta: Charles Matthews tuvo un día desafortunado en la línea de tiros libres ya que la probabilidad de que perdiera todos sus tiros libres fue de 0.0256 (solo había un 2.5 por ciento de posibilidades de que ocurriera ese evento).
   

   ¿Sientes el espíritu de March Madness? Vea nuestros consejos y trucos para completar un paréntesis, y lea por qué es tan difícil predecir trastornos y elegir un paréntesis perfecto.