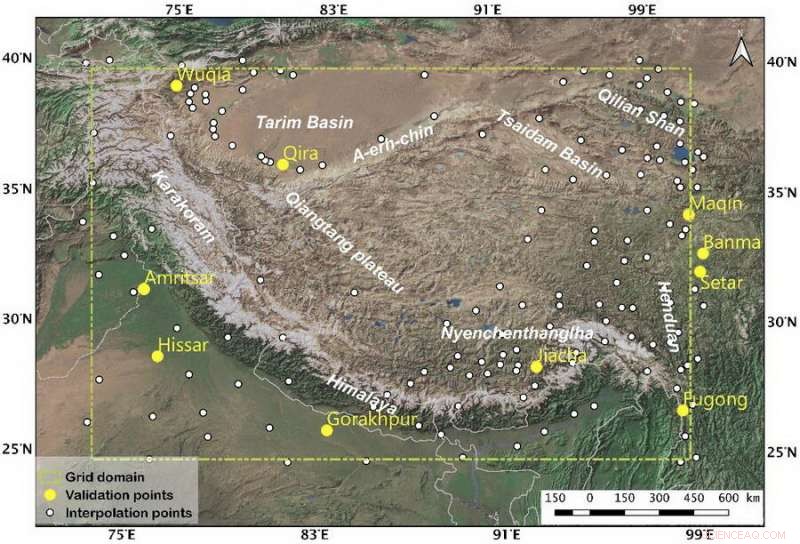
Fig. 1. El área de estudio y la distribución de los sitios de observación. Los diez puntos amarillos representan los sitios independientes utilizados para la validación de la distribución de frecuencia, y los puntos blancos representan los puntos para la cuadrícula. El rectángulo de puntos amarillos es la extensión de interpolación. Crédito:LI Hongyi
Un conjunto de datos precisos de precipitación en cuadrícula es esencial para una mejor comprensión del cambio climático, y procesos hidrológicos y ecológicos en la meseta tibetana. Sin embargo, la red de observación de precipitaciones en esta región es escasa. La precipitación observada es susceptible a complejas condiciones meteorológicas y orográficas, limitar la precisión del conjunto de datos de precipitación en cuadrícula. La variedad de instrumentos de precipitación en la meseta tibetana y áreas circundantes también ha afectado seriamente la corrección de la precipitación medida.
Al compensar la captura insuficiente de precipitación de diferentes tipos de instrumentos alrededor de la meseta tibetana y optimizar la distribución de la frecuencia de precipitación en el esquema de interpolación, un equipo de investigación del Instituto Noroeste de Ecoambiente y Recursos (NIEER) de la Academia de Ciencias de China (CAS) propuso un nuevo conjunto de datos de precipitación.
El conjunto de datos utiliza la precipitación observada de 159 estaciones como fuente de datos (Fig. 1) y corrige la captura insuficiente del medidor. Luego, comparando seis esquemas de interpolación comúnmente usados usando el error de frecuencia de precipitación como estándar de evaluación, Se obtiene el esquema de interpolación óptimo adecuado para la meseta tibetana.
Además, un conjunto de datos de precipitación en cuadrícula diaria con una resolución espacial de 10 km a partir del 1 de enero, 1980 al 31 de diciembre de 2009 se obtiene en base a esos trabajos.
Los resultados muestran que la corrección de la captura insuficiente es necesaria para los datos de la estación, lo que puede reducir el error de distribución en un 30% como máximo. Un algoritmo de interpolación de splines de placa delgada que considere la altitud como una covariable es útil para reducir el error de distribución estadístico en general.
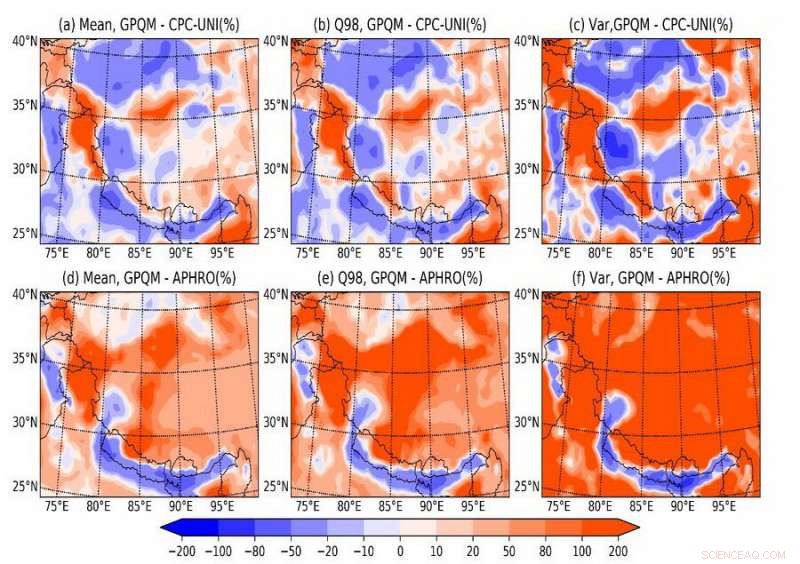
Fig. 2. La diferencia entre los resultados corregidos y el conjunto de datos anterior. La media es el promedio diario, Q98 es el percentil 98, Var es la varianza y APHRO significa el conjunto de datos APHRODITE. Todos los resultados consideran solo los días húmedos, que se clasifican por un umbral de 0,1 mm / d. La primera columna (a, d) muestra la diferencia en el promedio diario. La segunda columna (b, e) muestra la diferencia en el percentil 98 diario. La tercera columna (c, f) muestra la diferencia en la varianza diaria. Crédito:LI Hongyi
En comparación con el conjunto de datos de precipitación en cuadrícula existente, este conjunto de datos tiene mejores características de distribución de frecuencia de precipitación, un valor medio más razonable, diferencia, y un mejor efecto suavizante supresor que existe ampliamente en los productos de precipitación reticulados anteriores (Fig. 2).
Los resultados proporcionan un conjunto de datos de precipitación en cuadrícula relativamente confiable para esos estudios hidrometeorológicos en la meseta tibetana.
El conjunto de datos se ha publicado en línea en un artículo titulado "Reducción del error de distribución estadística en datos cuadriculados para la meseta tibetana" en el Revista de hidrometeorología .