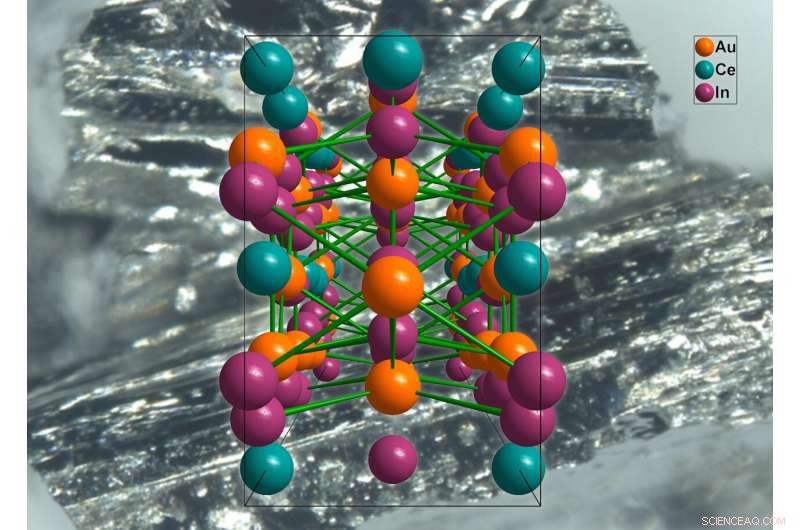
El nuevo material:Ce2 Au3 En5 . Crédito:Universidad Técnica de Viena
¿Cómo encuentra nuevos materiales con propiedades muy específicas, por ejemplo, propiedades electrónicas especiales que se necesitan para las computadoras cuánticas? Esta suele ser una tarea muy complicada:se crean varios compuestos, en los que se organizan átomos potencialmente prometedores en ciertas estructuras cristalinas, y luego se examina el material, por ejemplo, en el laboratorio de baja temperatura de TU Wien.
Ahora, una cooperación entre la Universidad Rice (Texas), TU Wien y otras instituciones internacionales de investigación ha logrado rastrear materiales adecuados en la computadora. Se utilizan nuevos métodos teóricos para identificar candidatos particularmente prometedores entre la gran cantidad de materiales posibles. Las mediciones en TU Wien han demostrado que los materiales tienen las propiedades requeridas y que el método funciona. Este es un importante paso adelante para la investigación de materiales cuánticos. Los resultados se han publicado ahora en la revista Nature Physics .
Semimetales topológicos
Rice University en Texas y TU Wien ya han trabajado juntos con mucho éxito en los últimos años en la búsqueda de nuevos materiales cuánticos con propiedades muy especiales:en 2017, los dos grupos de investigación presentaron el primer llamado "semimetal Weyl-Kondo", un material que potencialmente podría desempeñar un papel importante en la investigación de las tecnologías informáticas cuánticas.
"Los electrones en un material de este tipo no se pueden describir individualmente", explica la profesora Silke Bühler-Paschen del Instituto de Física del Estado Sólido de TU Wien. “Existen interacciones muy fuertes entre estos electrones, se interfieren entre sí como ondas según las leyes de la física cuántica, y al mismo tiempo se repelen debido a su carga eléctrica”.
Es precisamente esta fuerte interacción la que conduce a las excitaciones de los electrones, que solo pueden describirse utilizando métodos matemáticos muy elaborados. En los materiales que se estudian ahora, la topología también juega un papel importante:es una rama de las matemáticas que se ocupa de las propiedades geométricas que no cambian por la deformación continua, como el número de agujeros en una rosquilla, que permanece igual incluso si la la rosquilla está ligeramente exprimida.
De manera similar, los estados electrónicos en el material pueden permanecer estables incluso si el material se altera levemente. Esta es precisamente la razón por la que estos estados son tan útiles para aplicaciones prácticas como las computadoras cuánticas.
Uso de la computadora para identificar posibles candidatos
Calcular el comportamiento de todos los electrones que interactúan fuertemente en el material es imposible:ninguna supercomputadora en el mundo es capaz de hacerlo. Pero en base a hallazgos anteriores, ahora ha sido posible desarrollar un principio de diseño que utiliza cálculos de modelos simplificados combinados con consideraciones de simetría matemática y una base de datos de materiales conocidos para proporcionar sugerencias sobre cuál de estos materiales podría tener las propiedades topológicas teóricamente esperadas.
"Este método proporcionó tres candidatos de este tipo, y luego producimos uno de estos materiales y lo medimos en nuestro laboratorio a bajas temperaturas", dice Silke Bühler-Paschen. "Y, de hecho, estas primeras mediciones indican que es un semimetal topológico altamente correlacionado, el primero en ser predicho sobre una base teórica usando una computadora".
Una clave importante para el éxito fue explotar las simetrías del sistema de una manera inteligente:"Lo que postulamos fue que las excitaciones fuertemente correlacionadas todavía están sujetas a requisitos de simetría. Por eso, puedo decir mucho sobre la topología de un sistema sin recurriendo a cálculos ab initio que a menudo se requieren pero que son particularmente desafiantes para estudiar materiales fuertemente correlacionados", dice Qimiao Si de la Universidad de Rice. "Todo indica que hemos encontrado una forma sólida de identificar materiales que tienen las características que queremos". Método de demostración de físicos para diseñar metales topológicos