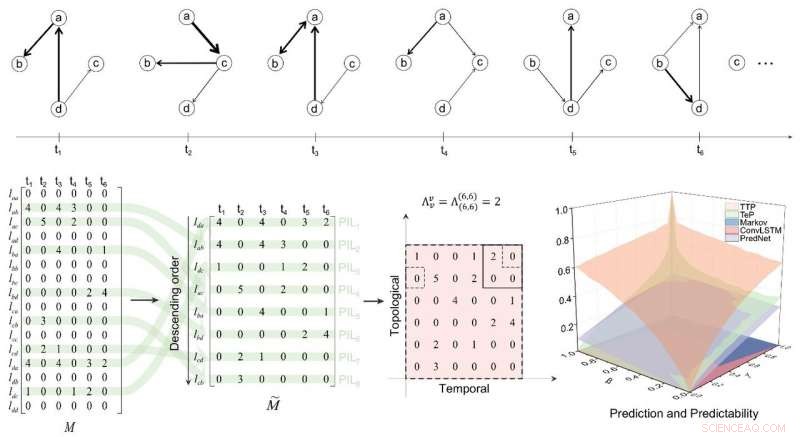
Cuantificar la previsibilidad de una red temporal. Crédito:Science China Press
Las redes o gráficos son descripciones matemáticas de la estructura interna entre los componentes de un sistema complejo, como las conexiones entre neuronas, interacciones entre proteínas, contactos entre individuos en una multitud, e interacciones entre usuarios en plataformas sociales en línea. Los enlaces en la mayoría de las redes reales cambian con el tiempo, y estas redes a menudo se denominan redes temporales. La temporalidad de los enlaces codifica el orden y la causalidad de las interacciones entre nodos y tiene un efecto profundo en la función de la red neuronal. propagación de enfermedades, agregación y recomendación de información, aparición de comportamiento cooperativo, y controlabilidad de la red. El aumento de la investigación se ha centrado en extraer los patrones en una red temporal y predecir su evolución futura utilizando técnicas de aprendizaje automático. especialmente graficar redes neuronales. Sin embargo, cómo cuantificar el límite de previsibilidad de una red temporal, es decir, el límite que ningún algoritmo puede superar, sigue siendo una pregunta abierta.
Recientemente, un equipo de investigación dirigido por Xianbin Cao con la Universidad de Beihang, Beijing, y Gang Yan en la Universidad de Tongji, Llevar a la fuerza, publicó un artículo titulado "Predecibilidad de las redes temporales reales" en Revista Nacional de Ciencias y propuso un marco para cuantificar la predictibilidad de redes temporales basado en la tasa de entropía de campos aleatorios.
Los autores mapearon cualquier red dada a una matriz de temporalidad-topología, y luego extendió el cálculo clásico de la tasa de entropía (que solo es aplicable a matrices cuadradas) a matrices arbitrarias a través de operadores de regresión. Las ventajas significativas de esta predictibilidad temporal-topológica fueron validadas en dos modelos típicos de redes temporales. Aplicando el método para calcular la predictibilidad de 18 redes reales, los autores encontraron que en diferentes tipos de redes reales, las contribuciones de la topología y la temporalidad a la predictibilidad de la red son significativamente variables; Aunque la línea de base teórica y la dificultad de la predictibilidad temporal-topológica son mucho más altas que las de las series de tiempo unidimensionales, la predictibilidad temporal-topológica de la mayoría de las redes reales es aún mayor que la de las series de tiempo.
El límite de previsibilidad calculado en esta investigación es una propiedad intrínseca de las redes temporales, es decir, es independiente de cualquier algoritmo predictivo, por tanto, también se puede utilizar para medir el posible espacio de mejora de los algoritmos predictivos. Los autores examinaron tres algoritmos predictivos ampliamente utilizados y encontraron que el rendimiento de estos algoritmos es significativamente más bajo que los límites predictivos en la mayoría de las redes reales. sugiriendo la necesidad de nuevos algoritmos predictivos que tengan en cuenta tanto las características temporales como las topológicas de las redes.