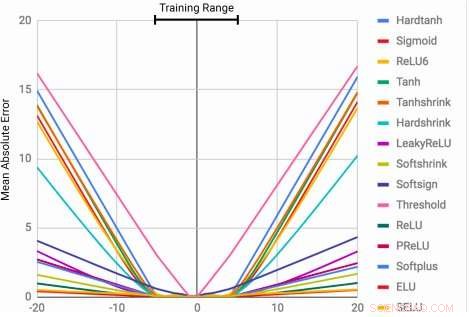
Los MLP aprenden la función de identidad solo para los valores de rango en los que están entrenados. El error medio aumenta considerablemente tanto por debajo como por encima del rango de números observados durante el entrenamiento. Crédito:Trask et al.
La capacidad de representar y manipular cantidades numéricas se puede observar en muchas especies, incluyendo insectos, mamíferos y humanos. Esto sugiere que el razonamiento cuantitativo básico es un componente importante de la inteligencia, que tiene varias ventajas evolutivas.
Esta capacidad podría ser muy valiosa en máquinas, lo que permite completar de forma más rápida y eficiente las tareas que implican la manipulación de números. Todavía, hasta aquí, Las redes neuronales entrenadas para representar y manipular información numérica rara vez han podido generalizar fuera del rango de valores encontrados durante el proceso de entrenamiento.
Un equipo de investigadores de Google DeepMind ha desarrollado recientemente una nueva arquitectura que aborda esta limitación, logrando una mejor generalización tanto dentro como fuera del rango de valores numéricos sobre los que se entrenó la red neuronal. Su estudio, que fue prepublicado en arXiv, podría informar el desarrollo de herramientas de aprendizaje automático más avanzadas para completar tareas de razonamiento cuantitativo.
"Cuando se entrena a las arquitecturas neuronales estándar para contar hasta un número, a menudo luchan por contar hasta uno más alto, "Andrew Trask, investigador principal del proyecto, le dijo a Tech Xplore. "Exploramos esta limitación y descubrimos que también se extiende a otras funciones aritméticas, lo que lleva a nuestra hipótesis de que las redes neuronales aprenden números de forma similar a como aprenden palabras, como un vocabulario finito. Esto les impide extrapolar correctamente funciones que requieren números (más altos) nunca antes vistos. Nuestro objetivo era proponer una nueva arquitectura que pudiera realizar una mejor extrapolación ".

El acumulador neuronal (NAC) es una transformación lineal de sus entradas. La matriz de transformación es el producto por elementos de tanh (Wˆ) y σ (Mˆ). La Unidad Lógica Aritmética Neural (NALU) utiliza dos NAC con pesos vinculados para permitir la suma / resta (celda púrpura más pequeña) y la multiplicación / división (celda púrpura más grande), controlado por una puerta (celda naranja). Crédito:Trask et al.
Los investigadores idearon una arquitectura que fomenta una extrapolación de números más sistemática al representar cantidades numéricas como activaciones lineales que se manipulan utilizando operadores aritméticos primitivos. que están controlados por puertas aprendidas. Llamaron a este nuevo módulo la unidad lógica aritmética neuronal (NALU), inspirado en la unidad lógica aritmética de los procesadores tradicionales.
"Los números generalmente se codifican en redes neuronales utilizando representaciones distribuidas o one-hot, y las funciones sobre números se aprenden dentro de una serie de capas con activaciones no lineales, "Trask explicó." Proponemos que los números se almacenen como escalares, almacenando un solo número en cada neurona. Por ejemplo, si quisieras almacenar el número 42, debería tener una neurona que contenga una activación de exactamente 42, 'en lugar de una serie de neuronas 0-1 que lo codifican ".
Los investigadores también han cambiado la forma en que la red neuronal aprende funciones sobre estos números. En lugar de utilizar arquitecturas estándar, que puede aprender cualquier función, idearon una arquitectura que propaga hacia adelante un conjunto predefinido de funciones que se consideran potencialmente útiles (por ejemplo, adición, multiplicación o división), utilizando arquitecturas neuronales que aprenden los mecanismos de atención sobre estas funciones.
"Estos mecanismos de atención deciden entonces cuándo y dónde se puede aplicar cada función potencialmente útil en lugar de aprender esa función en sí misma, ", Dijo Trask." Este es un principio general para crear redes neuronales profundas con un deseable sesgo de aprendizaje sobre las funciones numéricas ".

(arriba) Fotogramas de la tarea de seguimiento del tiempo de gridworld. El agente (gris) debe moverse al destino (rojo) a una hora especificada. (abajo) NAC mejora la capacidad de extrapolación aprendida por los agentes de A3C para la tarea de datación. Crédito:Trask et al.
Su prueba reveló que las redes neuronales mejoradas con NALU podrían aprender a realizar una variedad de tareas, como el seguimiento del tiempo, realizar funciones aritméticas sobre imágenes de números, traducir el lenguaje numérico a escalares de valor real, ejecutar código de computadora y contar objetos en imágenes.
En comparación con las arquitecturas convencionales, su módulo logró una generalización significativamente mejor tanto dentro como fuera del rango de valores numéricos que se le presentó durante el entrenamiento. Si bien NALU puede no ser la solución ideal para todas las tareas, su estudio proporciona una estrategia de diseño general para crear modelos que se desempeñen bien en una clase particular de funciones.
"La noción de que una red neuronal profunda debe seleccionar de un conjunto predefinido de funciones y aprender los mecanismos de atención que gobiernan dónde se utilizan es una idea muy extensible, "Trask explicó." En este trabajo, exploramos funciones aritméticas simples (suma, sustracción, multiplicación y división), pero estamos entusiasmados con el potencial de aprender los mecanismos de atención sobre funciones mucho más poderosas en el futuro, quizás trayendo los mismos resultados de extrapolación que hemos observado a una amplia variedad de campos ".
© 2018 Tech Xplore