
Figura 1:Expandiendo los vecindarios comenzando desde el nodo marrón en el medio. Primera expansión:verde; segundo:amarillo; tercero:rojo.
Una estructura de gráfico es extremadamente útil para predecir las propiedades de sus componentes. La forma más exitosa de realizar esta predicción es mapear cada entidad a un vector mediante el uso de redes neuronales profundas. Se puede inferir la similitud de dos entidades en función de la proximidad del vector. Un desafío para el aprendizaje profundo, sin embargo, es que uno necesita recopilar información entre una entidad y su vecindario expandido a través de capas de la red neuronal. El vecindario se expande rápidamente, haciendo la computación muy costosa. Para resolver este desafío, proponemos un enfoque novedoso, validado a través de pruebas matemáticas y resultados experimentales, que sugieren que es suficiente recopilar la información de solo un puñado de entidades aleatorias en cada expansión de vecindario. Esta reducción sustancial en el tamaño del vecindario brinda la misma calidad de predicción que las redes neuronales profundas de última generación, pero reduce el costo de capacitación en órdenes de magnitud (por ejemplo, 10 veces a 100 veces menos tiempo de cálculo y recursos), conduciendo a una escalabilidad atractiva. Nuestro artículo que describe este trabajo, "FastGCN:aprendizaje rápido con redes convolucionales gráficas mediante muestreo de importancia, "se presentará en ICLR 2018. Mis coautores son Tengfei Ma y Cao Xiao.
Complejidad del análisis de gráficos
Los gráficos son representaciones universales de relaciones por pares. En aplicaciones del mundo real, vienen en una variedad de formas, incluyendo por ejemplo, redes sociales, redes de expresión génica, y gráficos de conocimiento. Un tema de tendencia en el aprendizaje profundo es extender el notable éxito de arquitecturas de redes neuronales bien establecidas para datos estructurados euclidianos (como imágenes y textos) a datos estructurados irregularmente, incluyendo gráficos. La red convolucional gráfica, GCN, es uno de esos excelentes ejemplos. Generaliza el concepto de convolución para imágenes, que puede considerarse una cuadrícula de píxeles, a gráficos que ya no parecen una cuadrícula regular.
La idea detrás de GCN es muy simple. Aquellos de nosotros que tomamos Signal Processing 101 o un curso básico de visión por computadora ya estamos familiarizados con el concepto de un filtro de convolución. Para imágenes, es una pequeña matriz de números, para ser multiplicado por elementos con una ventana en movimiento de la imagen, con la suma del producto resultante reemplazando el número central de la ventana. Para gráficos, esto es similar. Una buena combinación de filtros puede detectar estructuras locales primitivas, como líneas en diferentes ángulos, bordes esquinas, y manchas de cierto color. Para gráficos, las convoluciones son similares. Imagine que cada nodo de la gráfica está inicialmente asociado con un vector. Para cada nodo, los vectores de los vecinos se suman (con ciertos pesos y transformaciones) en él. Por eso, todos los nodos se actualizan simultáneamente, realizando una capa de propagación hacia adelante. Las convoluciones de gráficos pueden usarse para propagar información a través de vecindarios de modo que la información global se difunda a cada nodo de gráfico.
El problema de GCN es que para una red con múltiples capas, el vecindario se expande rápidamente, involucrando muchos vectores para ser sumados, incluso para un solo nodo. Tal cálculo es prohibitivamente costoso para gráficos con una gran cantidad de nodos. ¿Qué tamaño tendrá un vecindario ampliado? En el análisis de redes sociales, hay un concepto famoso acuñado "seis grados de separación, "¡que establece que uno puede llegar a cualquier otra persona en la Tierra a través de seis conexiones intermedias! La Figura 1 ilustra que a partir del nodo marrón en el centro, expandiendo el vecindario tres veces (en el orden de verde, amarillo, y rojo) tocará casi todo el gráfico. En otras palabras, actualizar el vector del nodo marrón solo es problemático para un GCN con tan solo tres capas.
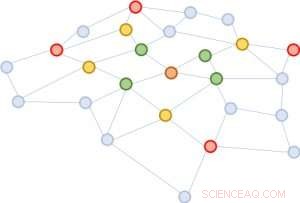
Figura 2:Partiendo del mismo nodo marrón, en cada expansión de barrio, solo muestreamos cuatro nodos.
Simplificando para la escalabilidad
Proponemos una solución simple pero poderosa, llamado FastGCN. Si expandir el vecindario por completo es costoso, ¿Por qué no ampliar solo unos pocos vecinos cada vez? La figura 2 ilustra el concepto. A partir del nodo marrón, en cada expansión elegimos un número constante (cuatro) de nodos y sumamos los vectores de ellos solamente. El muestreo reduce sustancialmente el costo de entrenamiento de la red neuronal, reduciendo el tiempo de entrenamiento en órdenes de magnitud en conjuntos de datos de referencia comúnmente utilizados por los investigadores. Todavía, las predicciones siguen siendo comparativamente precisas. El tamaño de estos gráficos de referencia varía desde unos pocos miles de nodos hasta unos cientos de miles de nodos, confirmando la escalabilidad de nuestro método.
Detrás de este enfoque intuitivo hay una teoría matemática para la aproximación de la función de pérdida. Una capa de la red se puede resumir como una multiplicación de matrices:H '=s (AHW), donde A es la matriz de adyacencia del gráfico, cada fila de H es el vector adjunto a los nodos, W es una transformación lineal de los vectores (también interpretada como el parámetro del modelo a aprender), y las filas de H 'contienen los vectores actualizados. Generalizamos esta multiplicación de matrices a una transformada integral h '(v) =s (òA (v, u) h (u) W dP (u)) bajo una medida de probabilidad P. Entonces, el muestreo de un número fijo de vecinos en cada expansión no es más que una aproximación de Monte Carlo de la integral bajo la medida P. La aproximación de Monte Carlo produce un estimador consistente de la función de pérdida; por eso, tomando el gradiente, podemos utilizar un método de optimización estándar (como el descenso de gradiente estocástico) para entrenar la red neuronal.
Una variedad de aplicaciones de aprendizaje profundo
Nuestro enfoque aborda un desafío clave en el aprendizaje profundo para gráficos a gran escala. Se aplica no solo a GCN sino también a muchas otras redes neuronales de gráficos basadas en el concepto de expansión de vecindario, un componente esencial del aprendizaje de la representación gráfica. Prevemos que la resolución del desafío en esta estructura de datos fundamental (gráficos) se adoptará en una amplia gama de aplicaciones, incluyendo el análisis de redes sociales, el conocimiento profundo de las interacciones proteína-proteína para el descubrimiento de fármacos, y la conservación y descubrimiento de información en bases de conocimiento.