¿Cuánta tensión sufren las tuberías cuando un líquido fluye a través de ellas y cómo depende del grado de curvatura de la tubería?

Las curvaturas de las tuberías son especialmente importantes, por ejemplo en el arco aórtico que conecta con el ventrículo izquierdo del corazón humano. Los sistemas de tuberías en plantas industriales a menudo incluyen curvas de 90 grados o más, pueden ser helicoidales e incluso pueden tener curvas de 180 grados. Los mecánicos de fluidos de Suecia han analizado el flujo de fluidos en este tipo de tuberías con una curva de 180 grados. Su investigación se publica en la revista Physical Review Fluids. .

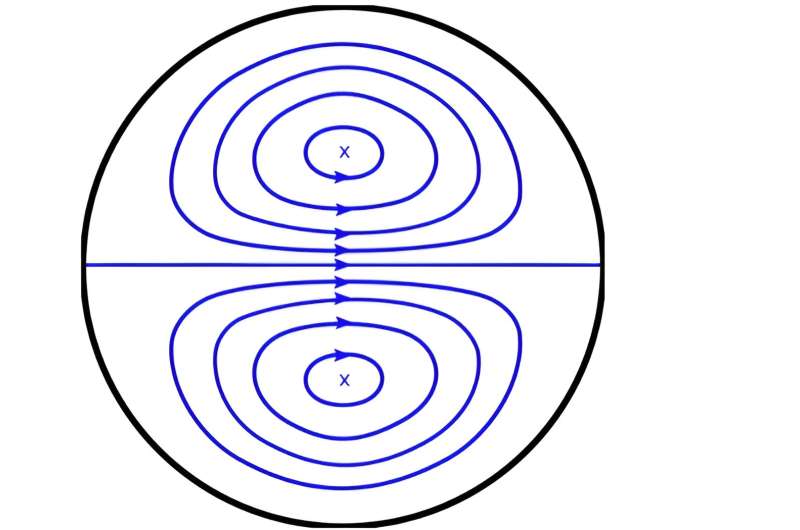
Los codos de las tuberías se diferencian de sus tramos rectos porque, en los tramos curvos, existen fuerzas centrífugas hacia afuera debido a la inercia del líquido en su interior. Esa fuerza se equilibra mediante un gradiente de presión desde la pared exterior de la tubería hasta la pared interior. Debido a que las velocidades del fluido en un corte imaginario a través de la tubería no serán iguales en la sección curva (por ejemplo, la velocidad cerca de la pared exterior de la tubería será mayor que cerca de la pared interior), un patrón de flujo secundario, además del movimiento a través la tubería, se instala perpendicular a la dirección principal del flujo.

Este movimiento es un par de vórtices simétricos y contrarrotativos, llamados vórtices Dean, en honor al científico británico William Reginald Dean, que aparecen en la primera curva de la tubería y pueden complicar el flujo posterior, tanto para flujo laminar como turbulento.

Para una sola curva, la geometría interna del flujo se puede describir mediante el número de Dean, que depende del radio de la tubería en relación con la cantidad de curvatura en la curva, y el número de Reynolds del fluido, que es la relación de fuerzas de inercia. a fuerzas viscosas dentro de un fluido. Los fluidos tienen un número de Reynolds crítico que caracteriza su transición de un flujo laminar suave a un flujo turbulento, y este puede ser dos veces mayor que en el flujo recto. (De hecho, el flujo turbulento de una tubería recta puede volver a ser laminar al entrar en una sección espiral de la tubería).

Aproximadamente, los números de Reynolds por debajo de 2.000 indican flujo laminar, los que están por encima de 3.500, flujo turbulento, con una transición de flujo laminar a turbulento que se produce en algún punto intermedio. El número Dean mide la intensidad del flujo secundario interno.

Daniele Massaro y sus colegas del KTH Royal Institute of Technology de Estocolmo utilizaron un método refinado para resolver numéricamente y computacionalmente las famosas y complicadas ecuaciones de fluidos de Navier-Stokes para analizar la transición (de flujo laminar a turbulento) en una tubería idealizada con una curvatura de 180. grados, comparando su hallazgo con resultados anteriores para codos (curva de 90 grados) y tubos toroidales.

Suponiendo una curvatura de tubería representativa de 1/3 (la relación entre el radio de una sección transversal de la tubería y el radio de curvatura), el grupo dividió el fluido simulado en aproximadamente 30 millones de rejillas, no todas uniformes. Luego resolvieron las ecuaciones de los puntos de la cuadrícula a medida que cambiaban con el tiempo.

Al realizar un análisis de estabilidad (que determina el crecimiento de imperfecciones diminutas e infinitesimales que aparecen en el fluido suave inicial), el cálculo determina los cambios en el fluido a medida que recorre la curva. Los cambios se producen a través de todas las secciones transversales verticales del fluido y a lo largo de la tubería. De esta forma se puede determinar la transición del flujo de laminar a turbulento.

El intenso cálculo (para el cual se necesitaban supercomputadoras, dijo Massaro, con ejecuciones que podrían llevar meses) encontró que el número de Reynolds crítico para la transición era 2.528. Esta es la región del número de Reynolds del fluido, independientemente del tipo, donde surge la inestabilidad y la forma de la estructura conduce a la transición a la turbulencia. Este punto de transición también se conoce como "bifurcación de Hopf". La inestabilidad de la curva de 180 grados se desarrolla de forma muy parecida a la de una curva de 90 grados. El número de Reynolds crítico para una curva de 90 grados es 2531 y para un toroide, 3290.

Debido a la naturaleza detallada de la inestabilidad, se espera que las tuberías con curvaturas superiores a 180 grados sean similares, hasta cierto punto. Para tuberías con curvaturas más cortas, la bifurcación de Hopf debe desaparecer a medida que el ángulo de curvatura se aproxima a cero y el flujo permanece laminar. El grupo estima que la bifurcación desaparece en una curva de unos 20 grados.

Aunque la investigación tiene aplicaciones industriales obvias, la extensión al corazón no es sencilla debido a la diferencia entre la sangre real y el flujo ideal de este estudio. "Nuestro estudio ayuda a comprender dónde podría ocurrir una transición repentina en el arco aórtico, generalmente laminar", dijo Massaro, coautor del estudio y estudiante de posgrado en el departamento de Ingeniería Mecánica del Instituto Real de Tecnología KTH en Estocolmo. . "De hecho, el régimen turbulento en la aorta puede estar relacionado potencialmente con diversas enfermedades del corazón."

Más información: Daniele Massaro et al, Estabilidad global del flujo de tubería con curvatura de 180∘ con adaptabilidad de malla, Revisión física de fluidos (2023). DOI:10.1103/PhysRevFluids.8.113903

Información de la revista: Líquidos de revisión física

© 2023 Red Ciencia X