La mayor parte de la informática en las redes neuronales de última generación comprende operaciones lineales, por ejemplo, multiplicaciones de matrices-vectores y convoluciones. Las operaciones lineales también pueden desempeñar un papel importante en la criptografía. Si bien hay procesadores dedicados, como GPU y TPU, disponibles para realizar operaciones lineales altamente paralelas, estos dispositivos consumen mucha energía y el bajo ancho de banda de la electrónica aún limita su velocidad de operación. La óptica es más adecuada para este tipo de operaciones debido a su paralelismo inherente y su gran ancho de banda y velocidad de cálculo.
Construido a partir de un conjunto de superficies delgadas diseñadas espacialmente, redes neuronales profundas difractivas (D 2 NN), también conocidas como redes difractivas, forman una arquitectura informática óptica de reciente aparición capaz de realizar tareas computacionales de forma pasiva a la velocidad de propagación de la luz a través de un volumen ultradelgado.
Estas computadoras totalmente ópticas para tareas específicas se diseñan digitalmente mediante el aprendizaje de las características espaciales de sus superficies difractivas constituyentes. Después de este proceso de diseño único, las superficies optimizadas se fabrican y ensamblan para formar el hardware físico de la red óptica difractiva.
En su publicación en Advanced Photonics Nexus , un equipo de investigadores dirigido por Aydogan Ozcan, profesor del Canciller y catedrático Volgenau de Innovación en Ingeniería de la UCLA, ha introducido un método para realizar operaciones lineales de valores complejos con redes difractivas bajo iluminación espacialmente incoherente.
El mismo grupo había demostrado previamente que las redes difractivas con suficientes grados de libertad pueden realizar transformaciones lineales arbitrarias de valores complejos con luz espacialmente coherente con un error insignificante.
Por el contrario, con luz espacialmente incoherente, estas redes pueden realizar transformaciones lineales arbitrarias de intensidades ópticas de entrada si los elementos de la matriz que definen la transformación son reales y no negativos. Dado que las fuentes de iluminación espacialmente incoherentes son más frecuentes y de más fácil acceso, existe una creciente necesidad de procesadores de difracción espacialmente incoherentes para manejar datos más allá de los valores no negativos.
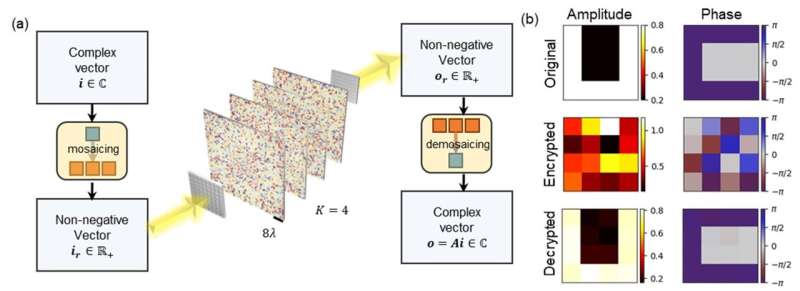
Al incorporar pasos de preprocesamiento y posprocesamiento para representar números complejos mediante un conjunto de números reales no negativos, los investigadores de UCLA han ampliado el poder de procesamiento de redes difractivas espacialmente incoherentes al dominio de los números complejos.
Demostraron que estos procesadores difractivos incoherentes pueden diseñarse para realizar una transformación lineal arbitraria de valores complejos con un error insignificante si hay un número suficiente de características difractivas optimizables de solo fase dentro del diseño, que se escala con las dimensiones del complejo de entrada y salida. espacios vectoriales.
Los investigadores mostraron la aplicación de este nuevo esquema mediante el cifrado y descifrado de imágenes de valores complejos utilizando redes difractivas espacialmente incoherentes. Además del cifrado de imágenes visuales, estos procesadores difractivos espacialmente incoherentes también podrían ser útiles en otras aplicaciones, por ejemplo, en vehículos autónomos para el procesamiento ultrarrápido y de bajo consumo de escenas naturales.
Más información: Xilin Yang et al, Transformaciones lineales universales de valores complejos y cifrado de imágenes utilizando redes difractivas espacialmente incoherentes, Advanced Photonics Nexus (2024). DOI:10.1117/1.APN.3.1.016010
Proporcionado por el Instituto de Ingeniería para el Avance Tecnológico de UCLA