La geometría está repleta de terminología que describe con precisión la forma en que varios puntos, líneas, superficies y otros elementos dimensionales interactúan entre sí. A veces son ridículamente complicados, como el rombicosidodecaedro, que creemos que tiene algo que ver con los agujeros de gusano o los polígonos de "Star Trek". ¿O qué tal el dodecaedro de 12 lados?

Otras veces, estamos dotados de términos más simples, como ángulos correspondientes .

Pero antes de explicar qué son, repasemos rápidamente algunos conceptos fundamentales.

Para empezar, ¿recuerdas la definición de ángulo? Es lo que obtienes cuando dos rayos (líneas con un único punto final) se unen en un punto. La distancia entre los dos rayos es el ángulo .

Líneas paralelas son dos líneas en un plano bidimensional que nunca se cruzan, sin importar cuán largas se vuelvan esas líneas.

Entonces, tenemos líneas transversales . Esta es simplemente una forma elegante de nombrar una línea que cruza al menos otras dos líneas.

Ahora nos estamos metiendo en la magia. Porque cuando una recta transversal cruza dos rectas paralelas, los ángulos que resultan de estas intersecciones son muy especiales. Es decir, los pares de ángulos del mismo lado de la transversal, y en la misma posición para cada línea que cruza la transversal, tienen el mismo ángulo. En otras palabras, esos ángulos son congruentes (lo mismo).

Si eso no está claro, tal vez la definición de Merriam-Webster ayude. Dice que los ángulos correspondientes son "cualquier par de ángulos, cada uno de los cuales está en el mismo lado de una de dos líneas cortadas por una transversal y en el mismo lado de la transversal".

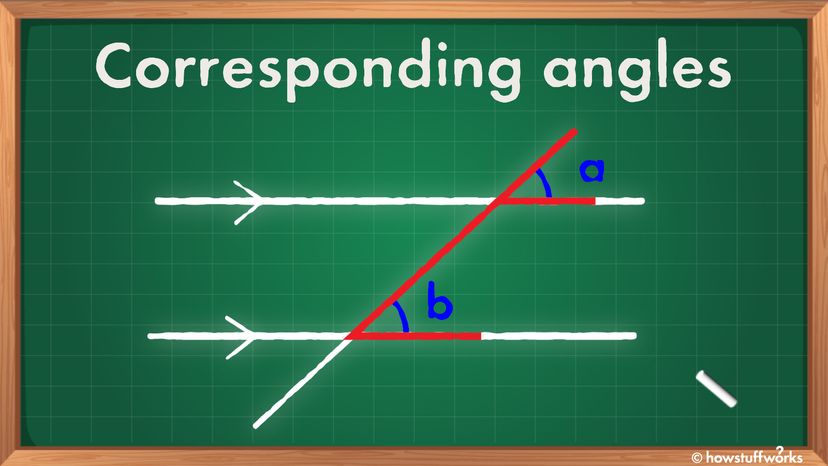
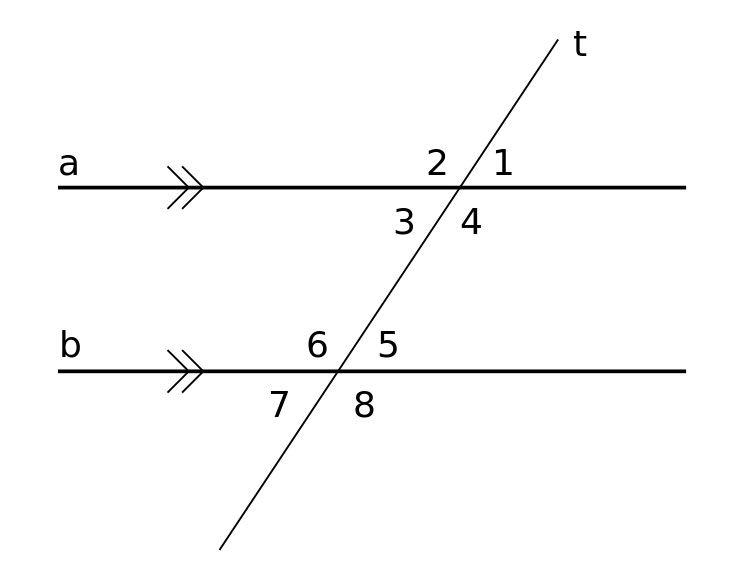
En la imagen principal de arriba, los ángulos correspondientes están etiquetados como "a" y "b". Tienen el mismo ángulo. Siempre puede encontrar los ángulos correspondientes buscando la formación F (ya sea hacia adelante o hacia atrás), resaltada en rojo. Aquí hay otro ejemplo en la imagen de abajo.

John Pauly es un profesor de matemáticas de secundaria que usa una variedad de formas para explicar los ángulos correspondientes a sus alumnos. Dice que a muchos de sus alumnos les cuesta identificar estos ángulos en un diagrama.

Por ejemplo, dice que tomemos dos triángulos similares, triángulos que tienen la misma forma pero no necesariamente el mismo tamaño. estas diferentes formas pueden ser transformadas. Es posible que hayan sido redimensionados, rotados o reflejados.

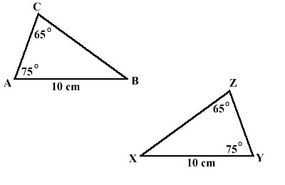
En ciertas situaciones, puedes asumir ciertas cosas sobre los ángulos correspondientes.

Por ejemplo, toma dos figuras que sean similares, lo que significa que tienen la misma forma pero no necesariamente el mismo tamaño. Si dos figuras son similares, sus ángulos correspondientes son congruentes (iguales). Eso es genial, dice Pauly, porque esto permite que las figuras mantengan su misma forma.

Dice que pienses en una imagen que quieras incluir en un documento. "Sabes que si cambias el tamaño de la imagen, tienes que tirar de una esquina determinada. Si no lo haces, los ángulos correspondientes no serán congruentes, en otras palabras, se verá torcido y desproporcionado. Esto también funciona para lo contrario. Si está tratando de hacer un modelo a escala, sabe que todos los ángulos correspondientes tienen que ser iguales (congruentes) para obtener la copia exacta que está buscando".

Ahora eso es interesante

Al igual que con todos los conceptos relacionados con las matemáticas, los estudiantes a menudo quieren saber por qué son útiles los ángulos correspondientes. "Bueno, si quieres asegurarte de que tienes dos líneas paralelas, puedes usar este pequeño truco", dijo Pauly. "¿Por qué no dibujar una línea recta que intercepte ambas líneas y luego medir los ángulos correspondientes?" Si son congruentes, sabrás que has medido y cortado correctamente las piezas. Conocer los ángulos correspondientes es útil cuando se construyen vías férreas, rascacielos y otras estructuras.