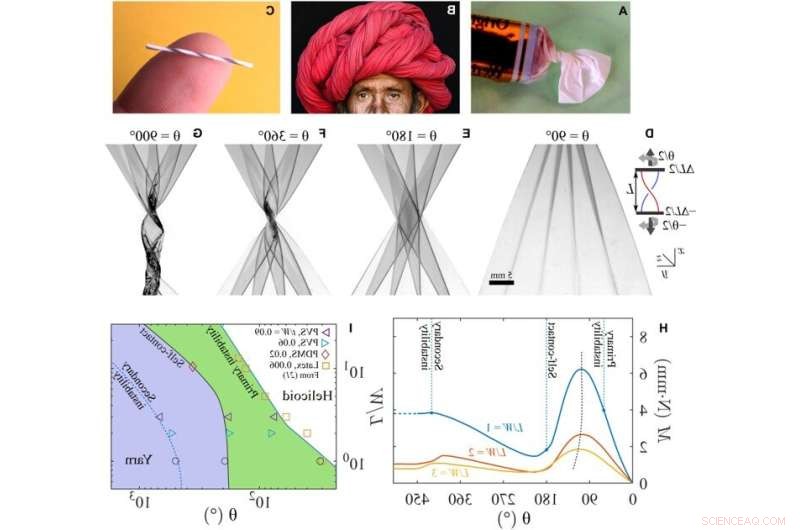
Los experimentos revelan una transformación muy ordenada de los hilos cuando las láminas que se mantienen bajo tensión se retuercen más allá del inicio de las inestabilidades primarias. Los siguientes son ejemplos de estructuras torcidas, plegadas y enrolladas:(A) caramelo envuelto, (B) turbante Rajashtani multifuncional (crédito de la foto:Lauren Cohen) y (C) hilo enrollado de una lámina de polietileno (consulte la sección S4). (D a G) Gráficos de sombras de una hoja de PDMS transparente retorcida en un ángulo θ como se muestra en el recuadro (L/W =1; t/W =0,0028; ΔL/L =0,1; θp =60 ± 5°). Recuadro:Esquema y sistema de coordenadas de laboratorio. (D) Arrugas observadas justo por encima del inicio de la inestabilidad primaria. (E) Hoja plegada en acordeón con autocontacto. (F) Un helicoide anidado con capas plegadas que se desarrollan a medida que la lámina se retuerce más. (G) La inestabilidad de pandeo secundario ocurre con más torsión, lo que da como resultado una estructura similar a un hilo. La barra de escala es la misma en (D) a (G). (H) El par medido muestra una variación de diente de sierra creciente y decreciente repetida con torsión. La amplitud de variación aumenta a medida que L/W disminuye. (I) Un mapa que delinea las regiones donde ocurren la inestabilidad primaria, el autocontacto y la inestabilidad secundaria en función de la relación de aspecto y la torsión. Las líneas son guías para el ojo, excepto la inestabilidad primaria para L/W> 3. Crédito:Science Advances (2022). DOI:10.1126/sciadv.abi8818
En un nuevo estudio publicado ahora como informe y también ilustrado como la portada en línea de Science Advances , Julien Chopin, Arshad Kudrolli y un equipo de investigación en Física de EE. UU. y Brasil demostraron cómo láminas hiperelásticas retorcidas formaban hilos autoenrollados de varias capas. Al incorporar el estiramiento dominante con la cinemática de plegado, midieron el par y la energía que se originaban en las no linealidades geométricas. Luego introdujeron un modelo geométrico para explicar la formación y la estructura de tales hilos autoenrollados. Los resultados mostraron cómo un simple giro de origami en el marco de torsión y plegado tensional condujo a la transformación de láminas estirables en arquitecturas autoensambladas.
Transformación de formas de hojas
Tradicionalmente, las láminas retorcidas pueden formar hilos funcionales que se basan en milenios de práctica humana para formar cuerdas de catgut, suturas quirúrgicas y prendas de vestir de tela; sin embargo, la práctica aún carece de principios generales que guíen la complejidad de tales arquitecturas. Los hilos enrollados con estructuras anidadas se pueden utilizar para aprovechar la energía de las baterías y para incrustar materiales amorfos. El plegado por torsión tensional puede transformar láminas planas en estructuras en capas a través de la regulación remota de límites. El plegado giratorio y el desplazamiento se pueden utilizar para reconfigurar y reutilizar hojas planas como se ve con el turbante multifuncional de Rajasthan.
Para comprender la transformación de forma de las láminas y la interacción entre la topología y las transformaciones de forma grande, Chopin y otros utilizaron escaneo de rayos X tridimensional para detallar la formación espontánea de hilos retorcidos de varias capas con arquitecturas internas ordenadas. Sin embargo, sigue siendo un desafío modelar las transformaciones y configuraciones de formas grandes. Estudios recientes han incorporado modelos de placas elásticas que incluyen la ecuación de Föppl-von Kármán (FvK) para resolver el crecimiento inicial por encima del inicio de la inestabilidad primaria, pero dichos métodos siguen explicando la transformación de una lámina plana en hilos enrollados. En este trabajo, Chopin et al desarrollaron un nuevo marco para combinar la cinemática de hojas estructuradas y usaron origami para explicar estas observaciones. El equipo mostró cómo las láminas plegadas mostraban formas poligonales regulares descritas por los símbolos de Schläfli y cómo la cinemática del origami capturó las principales características de la estructura para proporcionar un marco que sirvió como guía para desarrollar materiales hiperelásticos con amplias aplicaciones.
Portada en línea:Una hoja delgada de polidimetilsiloxano (PDMS) se retuerce en hilo enrollado de varias capas. Durante milenios, los humanos han torcido láminas estirables para formar hilos funcionales para crear prendas de vestir, instrumentos de cuerda y plástico reciclado. Chopin y Kudrolli, desarrollan un marco elasto-geométrico para comprender los mecanismos físicos involucrados en la torsión de láminas estirables en arquitecturas autoensambladas para estrategias de fabricación avanzadas. Crédito:Avances científicos (2022). DOI:10.1126/sciadv.abi8818
El equipo mostró ejemplos de láminas de polidimetilsiloxano (PDMS) con torsión creciente. A medida que la torsión aplicada aumentaba aún más, notaron la formación de una estructura helicoidal anidada en la cintura, seguida de inestabilidades secundarias y el resultante plegado recursivo y un hilo enrollado de múltiples capas. Cada transformación importante de la forma provocó que la tasa de cambio del par aplicado cambiara de signo y formara una variación en forma de diente de sierra con un giro.
Chopin et al ilustraron el marco de torsión tensional para comprender las principales etapas observadas de transformación de una hoja plana en hilos autoenrollados. Lo lograron mediante la introducción de un conjunto de modelos para combinar geometría, elasticidad y cinemática para luego capturar las transformaciones de forma observadas. Los investigadores capturaron la energía elástica almacenada y la respuesta torsional y siguieron este trabajo con tomografía de rayos X 3D para reconstruir láminas de polivinil siloxano (PVS) retorcidas. Luego, los científicos calcularon la densidad de energía de flexión utilizando láminas con varios módulos de Young y caracterizaron la transferencia con torsión.
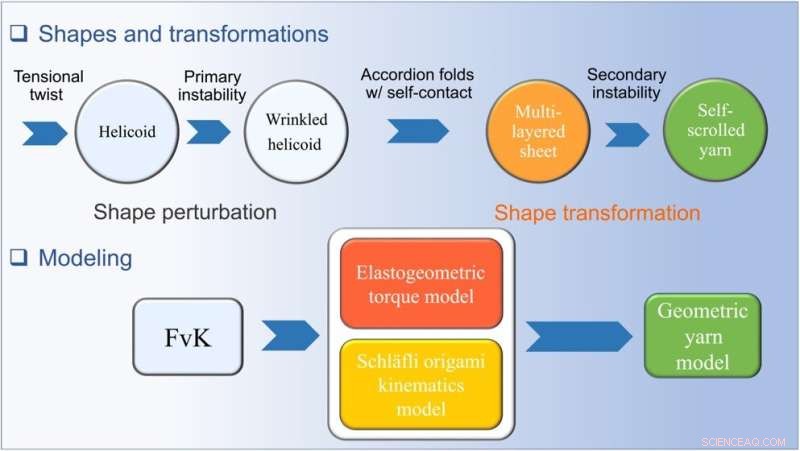
Una descripción general de las transformaciones de observación con torsión y el marco de plegado de torsión tensional. Las principales transformaciones observadas a medida que una hoja plana experimenta un plegado por torsión tensional y un desplazamiento con torsión aplicada. Se muestra el marco elastogeométrico, incluido el formalismo FvK perturbativo, el modelo de par elastogeométrico que incorpora no linealidades geométricas para explicar la relación tensión-deformación con torsión, el modelo cinemático de origami de Schläfli y el modelo de hilo geométrico. Crédito:Avances científicos (2022). DOI:10.1126/sciadv.abi8818
Modelo de torque elastogeométrico, autoplegable y origami Schläfli
Con base en las observaciones experimentales, Chopin et al desarrollaron un modelo elastogeométrico para calcular la energía elástica almacenada y la respuesta torsional de la lámina. Lo lograron inspirándose en la teoría del campo tensional para describir láminas altamente arrugadas, donde las tensiones de flexión y compresión eran insignificantes en comparación con las trenzas de tracción. Como en la teoría del campo tensional, Chopin et al asumieron que la energía durante el plegamiento estaba dada predominantemente por los modos de estiramiento en la dirección longitudinal, mientras que los modos de flexión eran subdominantes. El equipo comparó el par medido en función de la torsión en relación con la naturaleza hiperelástica del material y complementó su análisis elastogeométrico con la construcción de origami para mostrar una buena concordancia entre la forma de origami y la hoja torcida. Luego, los científicos identificaron estos origamis utilizando los símbolos de Schläfli, a los que luego llamaron Schläfli origami. Al variar los símbolos de Schläfli, Chopin y otros obtuvieron envolturas en forma de triángulo, pentágono, heptágono y nonágono. El trabajo destacó cómo la cinemática del origami apuntaló el plegado por torsión tensional.
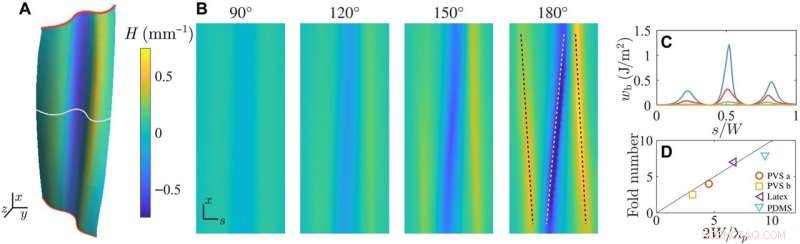
Plegado en acordeón a través de la localización de la curvatura. (A) La deformación de una hoja de polivinil siloxano (PVS) torcida por θ =120° obtenida con tomografía de rayos X y renderizada con curvatura media H dada por la barra de color a la derecha (L/W =3; t/W =0,009; θp =75° ± 5°). Se muestra el 80% central de la lámina lejos de las abrazaderas. (B) La distribución espacial H mapeada en un dominio rectangular muestra la ruptura de la simetría y la localización de la curvatura de la lámina con torsión. (C) El contenido de flexión wb muestra la localización de la energía con arrugas en la sección transversal indicada por la línea blanca sólida en (A). (D) El número medido de pliegues n comparado con la relación dada por la longitud de onda de la inestabilidad primaria n =2W/λp. Las relaciones de aspecto (t/W, L/W) son las siguientes:PVS a (0,009,2), PVS b (0,006,3), PDMS (0,003,1) y látex (0,003,2). Los tres materiales son hiperelásticos con módulo de Young E =1,2 MPa (PVS), 6,2 MPa (PDMS) y 3,6 MPa (látex). Crédito:Avances científicos (2022). DOI:10.1126/sciadv.abi8818
Formación del hilo y modelo geométrico del hilo
Para modelar el crecimiento del hilo, Chopin et al asumieron que la lámina podría dividirse en tres secciones, para incluir una estructura de longitud similar a un hilo y dos estructuras similares a un abanico. Esta simplificación les permitió conservar el papel fundamental del borde torcido de la hoja en el modelo de torque elastogeométrico. También estudiaron la evolución de la longitud del hilo envolviendo helicoidalmente los bordes del abanico alrededor de un núcleo cilíndrico de un diámetro específico para finalmente formar un modelo de crecimiento en buena concordancia con los datos experimentales.
El origami parcial de Schläfli explica las arquitecturas en capas a medio giro. (A) Formas geométricas obtenidas al aumentar los símbolos de Schläfli y el número de facetas. (B) Comparación del radiograma experimental y el origami de plegado de Schläfli. Se observa una buena correspondencia en los cuatro casos. (C) El ángulo Ψi del i-ésimo pliegue en función del ángulo calculado i α usando el modelo geométrico está en excelente acuerdo. (D) Comparación del ángulo del ápice α como función calculada α usando varias hojas y cargas. (E) El ángulo del vértice en función del número de triángulos es esencialmente constante. Crédito:Avances científicos (2022). DOI:10.1126/sciadv.abi8818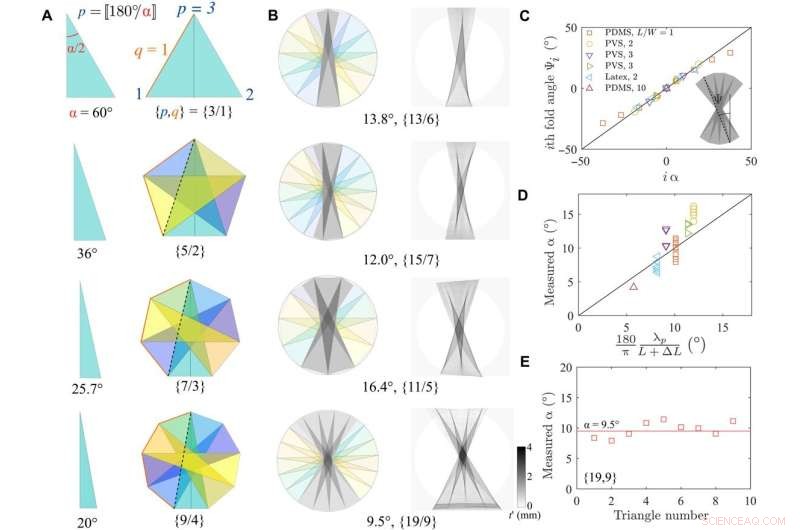
De esta manera, Julien Chopin, Arshad Kudrolli y sus colegas describieron la transformación notablemente ordenada de hojas planas en hilos enrollados de varias capas. Lo lograron mediante la introducción de una serie de modelos elastogeométricos simplificados para formar un marco de torsión y plegado tensional. El equipo exploró la estructura plana de varias capas mediante la introducción de un modelo de origami de Schläfli, en el que el origami, cuando se retorcía media vuelta, formaba polígonos regulares en forma de estrella caracterizados mediante símbolos de Schläfli. Chopin et al utilizaron el análisis de tomografía de rayos X para explicar la evolución de la hoja e indicaron la composición de una región de hilo altamente torcido en el centro y regiones en forma de abanico débilmente torcidas conectadas a las dos abrazaderas. El modelo incorporado en este trabajo se basó en una cinemática simplificada para proporcionar un marco que permita hilos multifuncionales que utilizan polímeros ultrafinos, nanotubos de carbono y láminas de grafeno, adecuados como materiales con aplicaciones en la medicina y la electrónica flexible. Los científicos utilizaron polímeros PDMS (polidimetilsiloxano) y PVS (polivinil siloxano) debido a su hiperelasticidad en diferentes condiciones de carga. La estrategia de plegado por torsión tensional resultante puede crear estructuras funcionales reubicables a partir de elementos simples para la fabricación avanzada con materiales blandos.
© 2022 Red Ciencia X Usar las matemáticas para describir la transición de hilado entre el ensamblaje de fibras en hilo