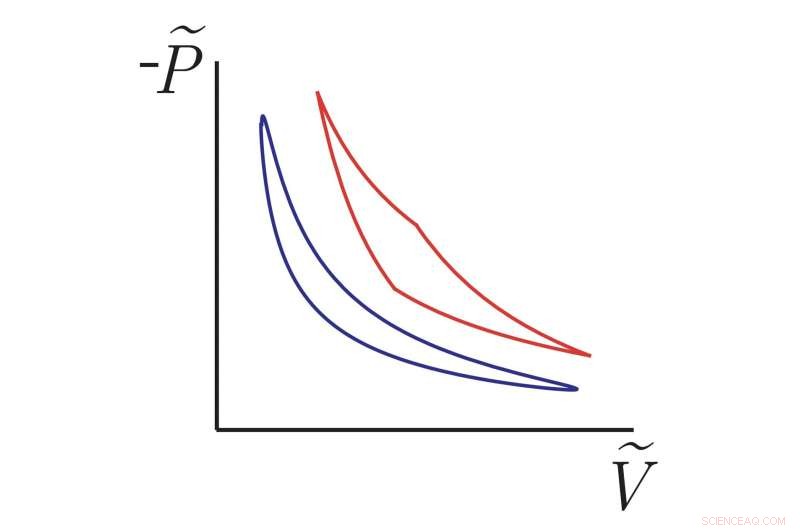
Los ciclos termodinámicos recientemente descubiertos (curva azul suave) se acercan a un límite geométrico novedoso en la eficiencia, superando a otros motores fuera del equilibrio como el ciclo de Carnot (curva roja) que opera en tiempo finito. Los ejes vertical y horizontal representan análogos de presión (negativa) y volumen para un motor microscópico que consiste en una partícula unida a un resorte que es sacudida por fluctuaciones térmicas de su entorno. Estas son curvas teóricas basadas en nuestros resultados matemáticos, pero los experimentadores han ideado recientemente métodos para medir la eficiencia de este tipo de sistemas para que nuestros resultados puedan probarse. Crédito:Frim &DeWeese.
La termodinámica estocástica es un área emergente de la física destinada a una mejor comprensión e interpretación de los conceptos termodinámicos fuera del equilibrio. En los últimos años, los hallazgos en estos campos han revolucionado la comprensión general de los diferentes procesos termodinámicos que operan en un tiempo finito.
Adam Frim y Mike DeWeese, dos investigadores de la Universidad de California, Berkeley (UC Berkeley), han llevado a cabo recientemente un estudio teórico que explora el espacio completo de los ciclos termodinámicos con una temperatura de baño que cambia continuamente. Sus resultados, presentados en un artículo publicado en Physical Review Letters , se obtuvieron utilizando métodos geométricos. La geometría termodinámica es un enfoque para comprender la respuesta de los sistemas termodinámicos mediante el estudio del espacio geométrico de control.
"Por ejemplo, para un gas en un pistón, una coordenada en este espacio de control podría corresponder al volumen del gas controlado experimentalmente y otra a la temperatura", dijo DeWeese a Phys.org. "Si un experimentador girara esas perillas, trazaría una trayectoria en este espacio termodinámico. Lo que hace la geometría termodinámica es asignar a cada curva una 'longitud termodinámica' correspondiente a la mínima energía disipada posible de un camino dado".
La geometría termodinámica permite a los investigadores examinar cuestiones de investigación interesantes, como la forma óptima de manipular un sistema nanoscópico dado, borrar un poco de información o construir un motor térmico clásico o cuántico.
"Nuestro principal objetivo en este documento era descubrir la forma más eficiente de hacer funcionar un motor microscópico para que produzca el trabajo más útil para la cantidad de combustible que consume", dijo DeWeese a Phys.org. "Mientras que la mayoría de los estudios de geometría termodinámica anteriores se centraban en optimizar el control de un sistema con una configuración inicial y final determinada, nosotros estábamos interesados en construir curvas cerradas óptimas que pudieran funcionar como motores térmicos altamente eficientes".
Las "reglas" principales para comprender cómo hacer funcionar de manera eficiente motores grandes, como los que se encuentran dentro de los automóviles, cuando se operan lentamente, se describieron por primera vez hace más de un siglo, cuando se formularon por primera vez las leyes de la termodinámica. En su artículo, Frim y DeWeese ampliaron estas teorías para que también pudieran aplicarse a motores microscópicos que funcionan en un tiempo finito. A diferencia de los motores grandes que funcionan lentamente, estos motores no están en equilibrio térmico con el mundo exterior y se ven fuertemente afectados por las fluctuaciones térmicas en el entorno circundante.
"En cualquier curso de termodinámica de pregrado, aprendemos que si graficas la presión frente al volumen de un gas en un cilindro y consideras cualquier ciclo cerrado que regresa al mismo punto en el gráfico, el área contenida dentro de la curva te da la cantidad útil trabajo que se obtiene de un ciclo de este motor térmico", dijo DeWeese. "Esto supone que te mueves muy lentamente alrededor del ciclo, de modo que el gas en el cilindro siempre permanece cerca del equilibrio con el mundo exterior. Hay una analogía con este diagrama P-V para motores microscópicos, como una pequeña partícula unida a un resorte. siendo azotado por las fluctuaciones térmicas de su entorno".
Cuando trazaron ciclos en el análogo de un diagrama P-V para un motor microscópico, Frim y DeWeese descubrieron que una función particular del área contenida dentro de la curva cerrada aún podía considerarse como la cantidad de trabajo útil proporcionado por un ciclo del motor. . Además, se encontró que la longitud de la curva cerrada está relacionada con la cantidad de "trabajo útil" que se ha perdido por disipación (es decir, calentar el ambiente sin ir hacia la operación del motor).
"Nuestro resultado es relativamente simple conceptualmente", explicó DeWeese. "En la geometría termodinámica, la longitud es algo así como la disipación. Entonces, pensamos:si tomas un ciclo (un ciclo cerrado) con un perímetro que tiene una longitud fija, ¿qué representa el área dentro de este ciclo? Resulta que va más o menos como la salida de trabajo del ciclo, por lo que en realidad, los ciclos óptimos deberían tener una disipación baja y un trabajo de salida alto, es decir, una longitud pequeña y un área grande".
Aprovechando los resultados geométricos clásicos, los investigadores pudieron identificar protocolos óptimos que establecieron un límite en la eficiencia de todos los ciclos cerrados. Sus hallazgos podrían contribuir significativamente al diseño y desarrollo de motores térmicos microscópicos eficientes. El límite de la eficiencia de los ciclos termodinámicos irreversibles establecido por este equipo de investigadores es general, por lo que sus implicaciones podrían ir mucho más allá de los motores microscópicos específicos considerados en su artículo.
"Uno de nuestros objetivos a largo plazo es desarrollar la teoría necesaria para que los ingenieros diseñen y construyan motores muy pequeños y eficientes", dijo DeWeese. "Esta podría convertirse en un área importante de la nanotecnología. También estamos muy motivados para comprender la estructura y función de los motores moleculares y otros tipos de 'máquinas' moleculares que vemos en las células de todas las criaturas y plantas". /P>
En su trabajo, De Weese y Frim plantean la hipótesis de que la evolución natural podría haber seleccionado máquinas moleculares eficientes. Si este fuera el caso, las reglas que descubrieron podrían ser un primer paso para poder predecir la estructura y función de las máquinas moleculares que son ubicuas en biología.
"Las desigualdades isoperimétricas (es decir, la interacción de longitudes y áreas de curvas cerradas) en los enfoques geométricos de la física podrían tener innumerables implicaciones en el futuro", agregó DeWeese. "Nuestro límite matemático es más realista que los resultados anteriores que suponían que el motor estaba muy cerca del equilibrio térmico con el medio ambiente (o baño de calor) en todo momento, pero aun así asumimos que el sistema funciona lentamente (es decir, los parámetros de control se cambian lentamente). Ahora estamos interesados en extender nuestros resultados más allá de este régimen para incluir sistemas más alejados del equilibrio".
© 2022 Red Ciencia X Los 'motores térmicos' miniaturizados podrían impulsar las máquinas a nanoescala del futuro