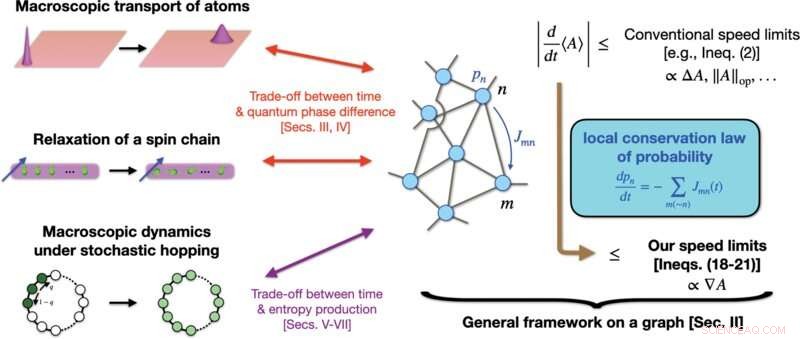
Ilustración esquemática de nuestros logros. Establecemos un marco general para derivar límites de velocidad cualitativamente más estrictos de una cantidad A que muchos convencionales, que dependen de toda la gama de A , como ΔA o ∥A ∥op . Nuestra estrategia es mapear la dinámica general de nuestro interés a la dinámica en un gráfico, donde usamos la conservación local de probabilidad. En contraste con los límites convencionales, nuestros límites de velocidad involucran el gradiente ∇A de A en el gráfico, lo que puede estrechar significativamente el límite cuando ∇A ≪ΔA o ∥A ∥op . Cuando se aplica a sistemas cuánticos macroscópicos (como el transporte macroscópico de átomos o la relajación de una cadena de espín perturbada localmente), nuestra teoría indica una nueva relación de compensación entre el tiempo y la diferencia de fase cuántica. Cuando se aplica a la dinámica estocástica macroscópica, incluida la cuántica, nuestra teoría indica una relación de compensación entre el tiempo y las cantidades, como la producción de entropía. Crédito:PRX Quantum (2022). DOI:10.1103/PRXQuantum.3.020319
Un físico teórico de RIKEN derivó una expresión para la velocidad máxima a la que pueden ocurrir cambios en los sistemas macroscópicos. Esto profundizará nuestra comprensión de los fenómenos cuánticos en sistemas que no están en equilibrio.
Uno de los aspectos más difíciles de comprender de la mecánica cuántica es el principio de incertidumbre de Heisenberg, que establece que no es posible precisar simultáneamente la posición y el momento de un objeto. En otras palabras, cuanto más precisamente se determina la posición de una partícula, más amplio se vuelve el rango de su posible momento (y viceversa).
En 1945, dos físicos, Leonid Mandelstam e Igor Tamm, se centraron en otro tipo de relación de incertidumbre, a saber, una entre el tiempo y la fluctuación de la energía, y demostraron que las transiciones en los sistemas cuánticos no ocurren instantáneamente; más bien, la velocidad a la que ocurre una transición está limitada por una cantidad determinada por cuánto fluctúa la energía del sistema.
Posteriormente se derivaron muchos otros llamados límites de velocidad cuánticos, que ayudaron a comprender mejor la física de los sistemas cuánticos y han sido útiles en diversas aplicaciones cuánticas.
Pero surgen grandes problemas cuando se aplican límites de velocidad cuánticos a sistemas macroscópicos. "Los límites de velocidad cuánticos anteriores, que son útiles para sistemas pequeños, por lo general pierden sentido para las transiciones macroscópicas", señala Ryusuke Hamazaki, del equipo de investigación RIKEN Hakubi de mecánica estadística cuántica sin equilibrio. "Por ejemplo, los límites de velocidad cuánticos convencionales dan un límite superior infinito para la velocidad de las transiciones en un gas formado por átomos".
Ahora, Hamazaki logró derivar un límite de velocidad cuántico para las transiciones en sistemas macroscópicos.
"Esta nueva derivación proporciona límites fundamentales que se pueden aplicar a varios tipos de fenómenos macroscópicos cuánticos fuera del equilibrio", dice. "Espero que aparezcan muchas leyes y aplicaciones fundamentales relacionadas con la dinámica cuántica macroscópica basadas en los conceptos presentados en este estudio".
Hamazaki derivó el límite de velocidad cuántica más estricto mediante el desarrollo de un marco general basado en la ley de conservación de la probabilidad, un principio fundamental de la física.
Un resultado inesperado para Hamazaki fue el descubrimiento de una nueva relación de compensación. "En lugar de una relación de compensación entre el tiempo y la fluctuación de la energía, como en el límite de Mandelstam-Tamm, encontré una entre el tiempo y el gradiente de la fase cuántica, una cantidad fundamental en la física cuántica".
Hamazaki ahora tiene la intención de extender su estrategia para ver si se puede usar para derivar límites de velocidad cuántica para cantidades como el crecimiento del entrelazamiento cuántico. Los límites de velocidad cuánticos no son realmente cuánticos