
Una configuración experimental para medir el efecto Hall convencional con un campo magnético perpendicular a la superficie. Crédito:FLOTA
Un estudio teórico de FLEET publicado esta semana ha encontrado una "pistola humeante" en la larga búsqueda del monopolo magnético topológico conocido como la curvatura de Berry.
Este descubrimiento es un gran avance en la búsqueda de efectos topológicos en sistemas que no están en equilibrio.
El grupo, dirigido por Dimi Culcer en UNSW, identificó un efecto Hall no convencional impulsado por un campo magnético en el plano en sistemas de orificios semiconductores, que se remonta exclusivamente a la curvatura Berry.
(En cambio, el efecto Hall ordinario y el efecto Hall anómalo requieren un campo magnético / magnetización que sea perpendicular a la superficie).
Los efectos topológicos mejorados permitirían que la electrónica topológica de baja energía sea viable para funcionamiento a temperatura ambiente, y se incluyeron recientemente en la hoja de ruta de IEEE hacia la electrónica del futuro.
Aislar la respuesta, un momento decisivo
"Aislar las respuestas topológicas en 'conductores regulares' ha sido una tarea históricamente difícil, ", dice el líder del equipo de investigación A / Prof Dimi Culcer (UNSW)." Aunque se cree que estas respuestas topológicas son ubicuas en los sólidos ".
Respuestas cuantificadas, como el efecto Hall cuántico y el efecto Hall de giro cuántico proporcionan una huella clara de la topología, sin embargo, estos solo se han observado en sistemas unidimensionales (1D) y están íntimamente conectados con la existencia de estados de borde.
En conductores 'regulares', es decir, sistemas 2D y 3D, Existe mucha literatura teórica que predice contribuciones topológicas a, por ejemplo, el efecto Hall anómalo, pero estos nunca se han observado de forma inequívoca en una medición de transporte.
Hay dos razones principales para esto:(i) los electrones de giro hacia arriba y hacia abajo generalmente hacen contribuciones opuestas, y estos casi se cancelan; (ii) lo que queda se ve abrumado por el desorden.
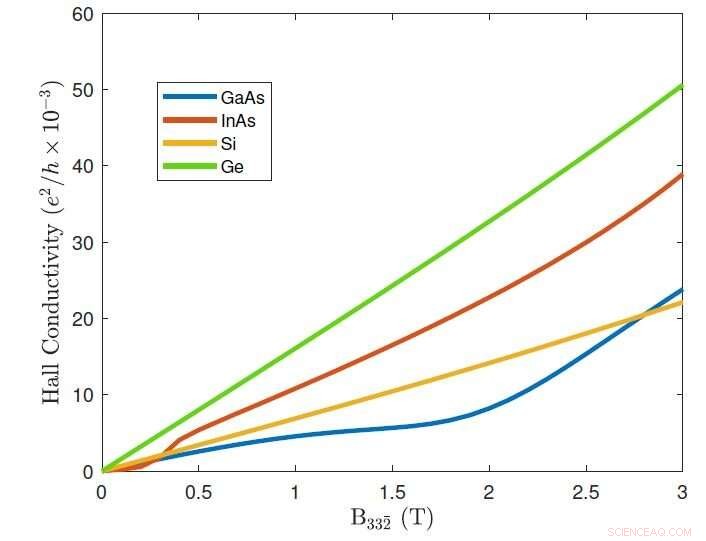
Respuesta de conductividad Hall al campo magnético. Crédito:FLOTA
El nuevo papel FLEET soluciona esta deficiencia de larga data identificando un sistema bidimensional en el que la curvatura Berry, y solo la curvatura Berry, es responsable de la señal de Hall lineal en el campo magnético aplicado en el plano.
"Notablemente, todas las contribuciones al desorden se desvanecen:no somos conscientes de ningún otro sistema multidimensional en el que esto sea cierto, "dice el autor principal, Doctorado en UNSW estudiante James Cullen. "Su medición experimental es accesible a cualquier laboratorio de vanguardia en todo el mundo, por lo tanto, esperamos un gran interés de los experimentadores ".
Curvatura de baya, el efecto Hall anómalo y los materiales topológicos
El equipo de investigación buscó el rastro matemático revelador llamado "Curvatura de Berry, "que se puede entender si pensamos en el concepto de transporte paralelo que aparece de forma rutinaria en la geometría y la relatividad general.
"Piense en un vector como una flecha que colocamos en algún lugar de la superficie de un objeto sólido, "explica Dimi." Ahora movemos la flecha, asegurándose de que siempre apunte en el mismo ángulo a la superficie; esto es, de hecho, como un ser humano caminando por la superficie de la Tierra. Finalmente, llevamos la flecha al punto de partida después de haber dado la vuelta, y encontramos que, en general, apunta en una dirección diferente, ha girado mágicamente en algún ángulo. El tamaño de este ángulo está determinado por la curvatura de la superficie. "
En mecánica cuántica, en lugar de vectores tenemos funciones de onda, pero podemos describir la dinámica usando la misma imagen, y la curvatura se llama curvatura Berry.
El ángulo de rotación es reemplazado por la famosa fase Berry, nombrado en honor al físico matemático Prof Sir Michael Berry, quien formuló el problema en la década de 1980. Mas tarde, basándose en el trabajo del premio Nobel David Thouless, Qian Niu de UT Austin demostró que la curvatura Berry se comporta como el codiciado monopolo magnético, pero no en el espacio real. más bien en el espacio de impulso, que es el espacio en el que piensan la mayoría de los físicos de materia condensada.
La curvatura de Berry genera efectos topológicos en sistemas fuera de equilibrio porque cuando se aplica un campo eléctrico, se acelera un electrón, por lo que su impulso cambia. Cuando esto sucede, su función de onda cambia lentamente, de la misma manera que la 'flecha' gira en transporte paralelo, y como resultado de esta rotación gradual se genera una corriente transversal (Hall). Las relaciones de Onsager, que son fundamentales para la física del desequilibrio, decir que la corriente de Hall no disipa energía. El caso extremo es el efecto Hall anómalo cuántico (QAHE), una clave de efecto cuántico para la función de los materiales topológicos, en el que las corrientes de borde pueden fluir con una resistencia eléctrica efectivamente cero.
('Quantum' describe la transición de 'escalón' en la resistencia transversal (Hall), es decir, varía en pasos discretos en lugar de suavemente, mientras que 'anómalo' se refiere a la ocurrencia del fenómeno en ausencia de cualquier campo magnético aplicado).
Los investigadores buscan mejorar QAHE para proteger el comportamiento topológico a temperaturas más altas, permitiendo la electrónica topológica que sería viable para el funcionamiento a temperatura ambiente.
"La reducción significativa de la resistencia eléctrica que permite la temperatura ambiente QAHE nos permitiría reducir significativamente el consumo de energía en los dispositivos electrónicos, "dice Dimi.