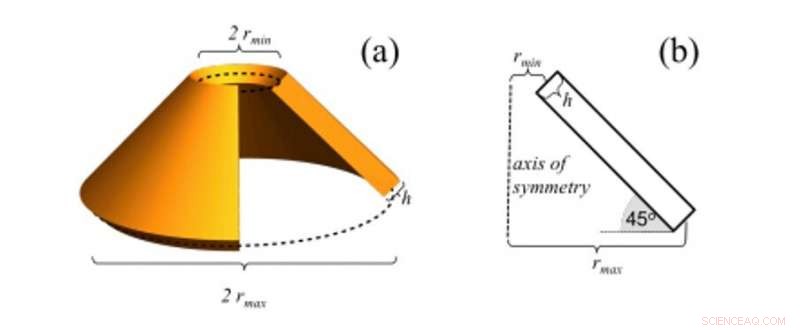
Un boceto del cono viscoelástico, y sus dimensiones. (a) Una vista en ángulo con una sección de la concha cónica cortada. (b) Un diagrama de sección transversal que incluya el eje de simetría y una sola sección de la carcasa cónica. Crédito:Science Advances, doi:10.1126 / sciadv.abb2948
Actualmente es un desafío determinar la estabilidad de las estructuras viscoelásticas ya que las conformaciones aparentemente estables pueden deslizarse gradualmente (deformación plástica de un material bajo tensión en función del tiempo) hasta que se pierde su estabilidad. Aunque un efecto de arrastre perceptible no conduce necesariamente a la inestabilidad de los sólidos viscoelásticos, Los investigadores actualmente están limitados con simulaciones numéricas para predecir la estabilidad futura en relación con las herramientas predictivas teóricas. En un nuevo informe sobre Avances de la ciencia , Erez Y. Urbach y Efi Efrati en física y sistemas complejos en el Instituto de Ciencias Weizmann, Israel, describió sólidos viscoelásticos a través de una métrica de referencia instantánea en evolución para medir las deformaciones elásticas. Los métodos transparentes e intuitivos derivados de este trabajo para sólidos viscoelásticos incompresibles redujeron la cuestión de la estabilidad futura a solo cálculos estáticos. El equipo demostró el poder predictivo del enfoque al comprender los mecanismos sutiles de la inestabilidad retardada en conchas elastoméricas delgadas para demostrar la concordancia cuantitativa con los experimentos.
Movimiento rastrero en la naturaleza
Un movimiento lento relativamente lento subyace a la trampa para moscas de Venus, uno de los movimientos más rápidos en el reino vegetal. Se observa una fluencia similar antes de que se rompan las carcasas elastoméricas delgadas, conocidos como poppers saltarines que duran una fracción de segundo. Mientras que el lento movimiento de las conchas parece ser elásticamente estable, órdenes de magnitud más duraderas, los de una escala mucho mayor se pueden observar en la corteza terrestre antes de la réplica de un terremoto. Los investigadores aún están aprendiendo el papel exacto de la viscoelasticidad en las réplicas debido a la ausencia de un marco teórico predictivo para detectar la estabilidad futura de dichos sistemas. En cada uno de los ejemplos descritos, el lento flujo viscoelástico en el material puede llevar al sistema a inestabilidades, provocando una liberación abrupta de energía elástica almacenada internamente. Aunque los científicos pueden determinar las variables que gobiernan el comportamiento viscoelástico, los mecanismos de las inestabilidades retardadas en los fluidos viscoelásticos siguen siendo poco conocidos. En este trabajo, Urbach y Efrati abordaron cuantitativamente la característica de inestabilidad viscoelástica mediante el uso de una descripción métrica.
Representación esquemática de la colinealidad de las métricas. La minimización de la métrica g (marcada por un círculo negro completo) está restringida y se realiza con respecto al subconjunto de métricas que corresponden a configuraciones realizables (línea negra gruesa). Estas métricas están en, especial, orientación conservando y euclidiana. Dada una métrica de referencia instantánea, g¯ (marcado por un círculo gris completo), la métrica realizada corresponderá al punto más cercano del conjunto de métricas admisibles a g¯ de acuerdo con la función de distancia dada por la energía elástica instantánea. Partiendo del descanso g¯ evoluciona de g¯0 (marcado por un círculo rojo completo) hacia g, que sigue siendo la métrica admisible más cercana a g¯ debido a la colinealidad de las tres métricas. Como g permanece estacionario, la evolución de g¯ preservará la colinealidad, acercándose asintóticamente a g¯stat (marcado por un círculo abierto), que también es colineal. Destacamos que a lo largo de esta evolución, g permanece sin cambios; por lo tanto, no se observará variación de la configuración a pesar de la relajación de la tensión. Crédito:Science Advances, doi:10.1126 / sciadv.abb2948 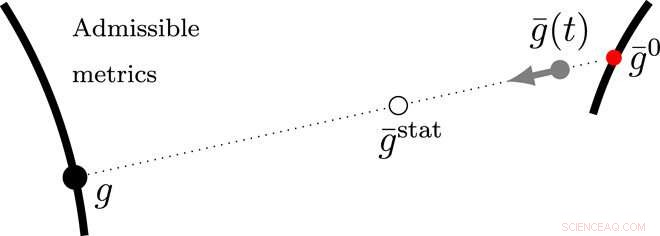
El equipo describió el comportamiento de los materiales como una respuesta elástica rápida en relación con las longitudes de prueba que evolucionan temporalmente y que pueden cambiar debido al flujo viscoelástico lento. Interpretaron la respuesta microscópica en el material y predijeron la estabilidad futura de las estructuras viscoelásticas sin restricciones. Urbach y col. explicó todas las relaciones de los materiales viscoelásticos lineales a través de intrincados cálculos de la velocidad de deformación con una función de relajación de la tensión, luego derivó relaciones matemáticas para sistemas unidimensionales en este trabajo; algunos de los cuales dependían de las propiedades del material, como el módulo de Young y la relación de Poisson. Las deformaciones incrementales instantáneas causaron un aumento de la tensión lineal para una respuesta puramente elástica en el material. Dado que los materiales viscoelásticos tienden a ser disipativos (termodinámicamente abiertos), la definición de energía libre elástica puede ser incompleta. Por lo tanto, los científicos eliminaron la inercia del sistema y aproximaron el movimiento del material a un cuasi-estado que evoluciona entre estados de equilibrio elástico. Como resultado, una métrica de referencia instantánea dada podría producir múltiples configuraciones elásticamente estables.
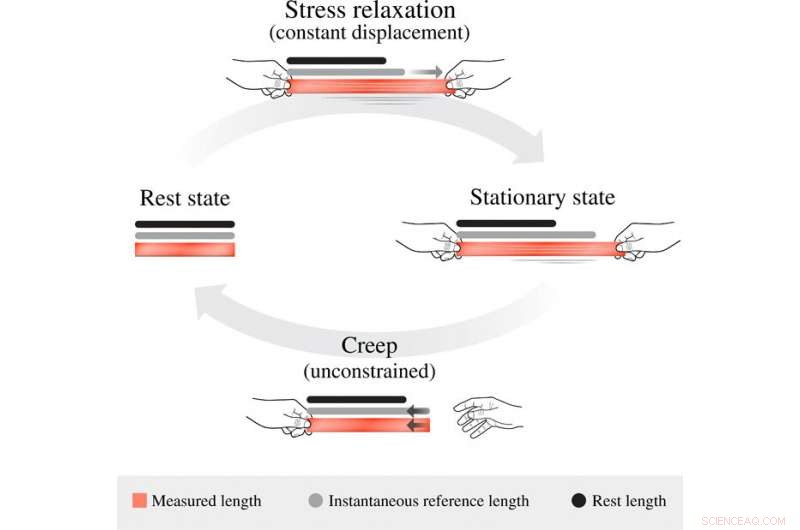
La evolución de la longitud de referencia viscoelástica. En el estado de reposo, las tres medidas de longitud en el cuerpo, su longitud medida g (marcada en rojo), su longitud de referencia instantánea g¯ (marcada en gris), y su longitud de referencia en reposo g¯0 (marcada en negro) son todas iguales. Cuando se somete a una extensión de desplazamiento constante, la longitud de referencia instantánea evoluciona alejándose de la longitud en reposo y hacia la longitud actualmente asumida, resultando así en la relajación del estrés. Se aproxima asintóticamente al estado estacionario g¯stat =βg + (1 − β) g¯0, en el que la tensión inicial se reduce en un factor de 1 - β. Cuando se libera, el sistema no restringido adopta inmediatamente su longitud de referencia instantánea preferida, cuales, Sucesivamente, se arrastra gradualmente hacia las longitudes de descanso. Crédito:Science Advances, doi:10.1126 / sciadv.abb2948
Inestabilidades viscoelásticas a través de la descripción métrica
La métrica de referencia instantánea dependiente del tiempo del material podría de esta manera evolucionar para adquirir nuevas configuraciones estables, fusionar puntos estables existentes, o hacer que las configuraciones elásticas estables pierdan estabilidad. En el último escenario, la lenta evolución viscoelástica será seguida por un chasquido rápido, lo que destaca la principal dificultad de predecir la estabilidad de las estructuras viscoelásticas. Esta característica se conoce como biestabilidad temporal, pseudo biestabilidad o pandeo por fluencia. Deben tener lugar dos procesos distintos para que los sólidos linealmente viscoelásticos incompresibles se introduzcan en la inestabilidad. Primero, un estado elásticamente estable adquirirá estabilidad a través de la relajación viscoelástica bajo alguna carga externa durante un período de tiempo. Luego, a medida que se quita la carga externa, el cuerpo asumirá el estado estable recién adquirido, junto con la fluencia viscoelástica para la inestabilidad resultante. Sin embargo, un estado estable adquirido es transitorio (temporal). De este modo, Urbach y col. utilizó la descripción métrica de la viscoelasticidad para proporcionar una imagen del mecanismo que gobierna la estabilidad de las estructuras viscoelásticas.
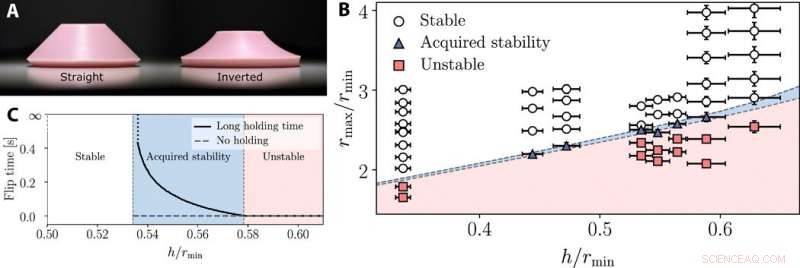
Verificación experimental del diagrama de estabilidad viscoelástica. (A) Poppers cónicos rectos e invertidos. Crédito de la foto:Erez Y. Urbach, Instituto Weizmann. (B) Los dos ejes abarcan las propiedades geométricas adimensionales de los poppers cónicos truncados. Los colores de fondo representan las regiones predichas teóricamente de cada una de las fases. Cada marcador corresponde a un popper diferente; Los marcadores de diferentes formas (y colores) indican las diferentes fases observadas en el experimento. (C) Tiempo de volteo calculado numéricamente en función del espesor normalizado del popper cónico para una liberación inmediata y un tiempo de retención prolongado. Los diferentes poppers se simularon variando sus espesores y radios constantes rmin =10 mm, rmáx =25 mm. Las propiedades del material tomadas fueron β =0,1, y se asumió que el núcleo de memoria era exponencial con τ =0.1 s, Módulo de Young E =2.5 MPa, y la razón de Poisson v =0.47. La variación del kernel puede provocar una variación en la tasa de divergencia del tiempo de cambio entre la región de estabilidad estable y adquirida, sin embargo, la ubicación de esta divergencia permanecerá sin cambios. La divergencia de los tiempos de inversión se abordó en un estudio anterior, y más recientemente, la tasa de divergencia también se estudió previamente. Crédito:Science Advances, doi:10.1126 / sciadv.abb2948
Resultados experimentales
Los cálculos realizados en este trabajo revelaron muchas características cualitativas de las inestabilidades viscoelásticas. Luego, los científicos probaron las predicciones cuantitativas de la teoría examinando experimentalmente la respuesta de los poppers cónicos de caucho de silicona. Para esto, Fundieron poppers de caucho de silicona como conchas cónicas truncadas para obtener un control más simple sobre el espesor del material. A medida que aumentaba el espesor, la biestabilidad disminuyó, luego, en un momento determinado, el popper respondió de inmediato. Los científicos produjeron 50 poppers cónicos diferentes de diferentes geometrías y probaron sus fases para determinar experimentalmente los límites de fase de las propiedades viscoelásticas.
El trabajo presentado aquí fue similar a estudios previos sobre elastoplasticidad. La teoría métrica se puede implementar en sólidos viscoelásticos incompresibles isotrópicos para proporcionar reglas básicas para las inestabilidades viscoelásticas. Para que una estructura dada se deslice hacia la inestabilidad, el arrastre debería haber precedido dentro de un período de tiempo en el que las estructuras se mantuvieron bajo una carga externa. La teoría fue especialmente poderosa en la aplicación para describir la inestabilidad retardada experimentalmente en conchas elastoméricas delgadas. Estos resultados podrán arrojar luz sobre el papel de la viscoelasticidad en el desencadenamiento de réplicas tardías del terremoto. De este modo, La descripción métrica propuesta aquí proporcionará un marco teórico para comprender las inestabilidades viscoelásticas retardadas.
© 2020 Science X Network