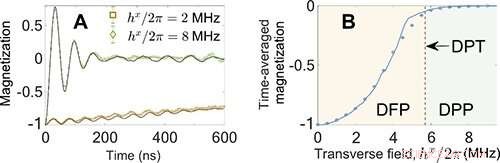
Fig. 1 Evolución temporal de la magnetización y magnetización promediada en el tiempo en función del campo transversal. Crédito:IOP
La simulación cuántica utiliza un sistema cuántico controlable para imitar sistemas complejos o resolver problemas intratables. entre los cuales los problemas de no equilibrio de los sistemas cuánticos de muchos cuerpos han atraído un amplio interés de investigación. Estos sistemas son difíciles de simular con computadoras clásicas. En lugar de, simuladores cuánticos populares, como circuitos superconductores, puede proporcionar información sobre estos problemas. Dado que se han realizado avances considerables en escalabilidad, coherencia y controlabilidad, Los circuitos superconductores se han convertido en una de las plataformas de simulación cuántica más importantes.
Recientemente, un grupo de investigación del Instituto de Física de la Academia de Ciencias de China, Universidad de Zhejiang y RIKEN en Japón, ha realizado con éxito la simulación cuántica de transiciones de fase dinámicas en un modelo de Lipkin-Meshkov-Glick con un simulador cuántico superconductor de 16 qubit.
La transición de fase dinámica (DPT) es una especie de transición de fase sin equilibrio y se ha investigado teóricamente en varios modelos cuánticos de muchos cuerpos. Hay dos tipos de TED. El primer tipo (DPT-1) se centra en el parámetro de orden de no equilibrio, mientras que el segundo tipo (DPT-2) se caracteriza por los comportamientos no analíticos del eco de Loschmidt asociado con los ceros de Lee-Yang-Fisher en mecánica estadística. Otras investigaciones teóricas y numéricas han revelado que DPT-1 y DPT-2 pueden estudiarse en el mismo marco.
El procesador cuántico integra 20 qubits superconductores, todos acoplados a un bus resonador común, que se utilizó para generar estados del gato de Schrödinger en trabajos anteriores. Esta vez, Se utilizaron 16 qubits para diseñar el modelo de Lipkin-Meshkov-Glick (LMG) aplicando un campo transversal controlable a cada qubit. El sistema se conduce a un estado de no equilibrio con microondas y luego evoluciona bajo el modelo LMG.
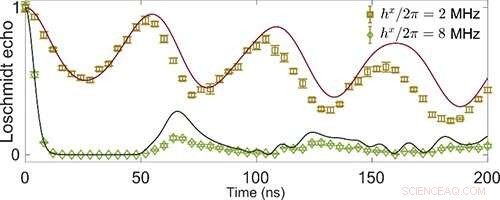
Fig. 2 Evolución temporal del eco de Loschmidt. Crédito:IOP
Los investigadores observaron por primera vez las características típicas del DPT-1. Para el pequeño campo transversal, el sistema permanece en la fase ferromagnética dinámica (DFP), y la magnetización exhibe una relajación lenta. Sin embargo, dado un fuerte campo transversal, el sistema entra en la fase paramagnética dinámica (DPP), en el que la magnetización exhibe una gran oscilación en un tiempo temprano y se acerca a cero en el límite de tiempo largo. La magnetización promediada en el tiempo como parámetro de orden de no equilibrio es cero en el DPP, mientras que se vuelve finito en el DFP.
Luego demostraron la existencia de los ceros del eco de Loschmidt en el DPP, sugiriendo la relación entre DPT-1 y DPT-2. Además, los investigadores exploraron las DPT desde una perspectiva novedosa. Estudiaron la compresión de espín mínimo como una sonda de la transición de fase.
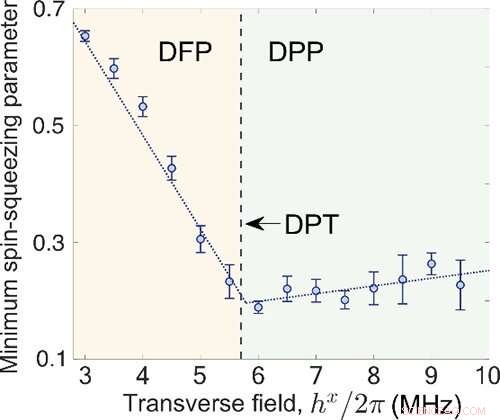
Fig. 3 El parámetro mínimo de compresión de giro en función del campo transversal. Crédito:IOP
Los resultados experimentales muestran que el valor mínimo de los parámetros de compresión de giro se puede lograr muy cerca del punto crítico del DPT. Esto indica una posible aplicación del DPT a la metrología cuántica.
Este estudio, titulado "Probar transiciones de fase dinámicas con un simulador cuántico superconductor, "fue publicado en Avances de la ciencia .