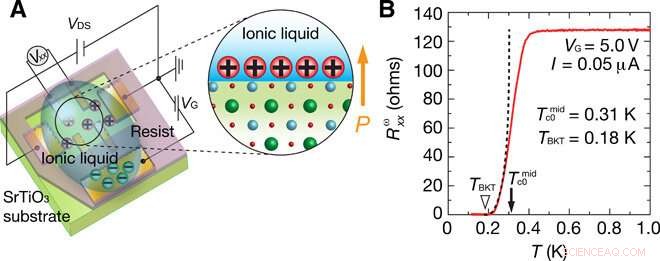
Imagen de dispositivo y superconductividad inducida por puerta en SrTiO3. (A) Imagen esquemática de SrTiO3-EDLT. (B) Primera resistencia armónica longitudinal Rωxx en función de la temperatura T bajo campo magnético cero. La corriente aplicada fue de 0.05 μA, que puede considerarse como límite de baja corriente. La temperatura de transición definida por el punto medio de la transición resistiva se estima como Tc0 =0.31 K (flecha negra). La línea discontinua negra muestra la curva de ajuste según la fórmula Halperin-Nelson, donde RN =128 ohmios es la resistencia en estado normal (T =1.0 K), b =1,17 es una constante adimensional, y TBKT =0,18 K es la temperatura de transición de BKT (triángulo blanco). El voltaje de puerta aplicado VG es 5.0 V a T =260 K. Crédito:Science Advances, doi:10.1126 / sciadv.aay9120
En ciencia de materiales, Los sistemas de electrones bidimensionales (2DES) realizados en la superficie o interfaz del óxido son un candidato prometedor para lograr nuevas propiedades físicas y funcionalidades en un campo cuántico que emerge rápidamente. Si bien 2-DES proporciona una plataforma importante para eventos cuánticos exóticos, incluido el efecto Hall cuántico y la superconductividad, el efecto de la ruptura de la simetría; transición de un estado desordenado a un estado más definido, sobre tales fases cuánticas siguen siendo esquivas. El transporte eléctrico no recíproco o la resistencia dependiente de la dirección de la corriente es una sonda para la simetría de inversión rota (presencia de un dipolo), como se observa en varios cristales e interfaces nocentrosimétricos. En un nuevo informe, Yuki M. Itahashi y un equipo de científicos en física aplicada, nanosistemas y ciencia de materiales en Japón y los EE. UU. informaron sobre el transporte no recíproco en la superficie de un superconductor 2-D hecho del material superconductor titanato de estroncio (SrTiO 3 ). El equipo observó una mejora gigantesca de la región no recíproca en la región de fluctuación superconductora, seis órdenes de magnitud mayor en comparación con su estado normal. Los resultados ahora se publican en Avances de la ciencia y demostrar características sin precedentes del superconductor polar bidimensional.
Los conductores polares o superconductores son plataformas de materiales potenciales para el transporte cuántico y las funcionalidades espintrónicas, con transporte no recíproco inherente que refleja la elusiva propiedad de romper la simetría de inversión del tiempo (es decir, romper la conservación de la entropía). Experimentos recientes se han extendido al estado superconductor para observar una gran respuesta no recíproca y los físicos están ansiosos por examinar la no reciprocidad en torno a la transición superconductora en un sistema electrónico simple. Para esto, Itahashi y col. electrodos de cromo / oro (Cr / Au) diseñados en la superficie atómicamente plana de SrTiO 3 y se colocó líquido iónico en la parte superior para formar un transistor eléctrico de doble capa (EDLT) para realizar un superconductor Rashba; basado en el efecto Rashba, con una técnica de activación de iones en SrTiO 3 superficie del material. Luego, los científicos midieron el transporte electrónico armónico primero y segundo utilizando una técnica de bloqueo estándar para medir el transporte de carga no recíproco y cuantificar la ruptura de la simetría de inversión del tiempo en el sistema. El transporte no recíproco también es una herramienta eficaz para identificar pares de Cooper, donde un par de electrones superan su repulsión habitual para compartir un estado cuántico de paraconductividad no recíproca en superconductores, que Itahashi et al. también pretende cuantificar en el superconductor Rashba.
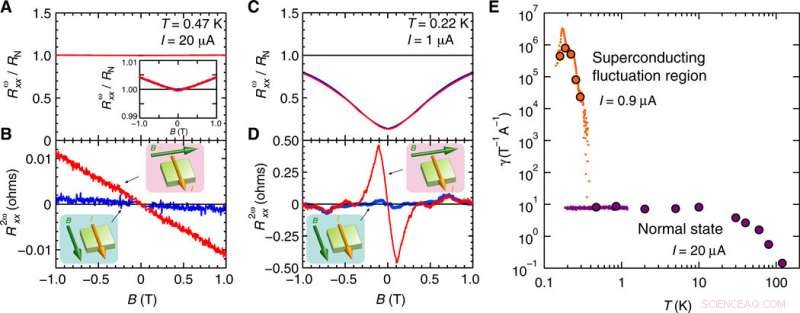
Magnetotransporte de SrTiO3 2D inducido por la puerta para los estados normal y superconductor y mejora del transporte no recíproco en la región de fluctuación superconductora. (A) Magnetorresistencia armónica primero y (B) segundo (Rωxx y R2ωxx, respectivamente) por encima de Tc0 (estado normal, T =0.47 K e I =20 μA) como una función del campo magnético en el plano B perpendicular (rojo) o paralelo (azul) a I.Los recuadros en (A) y (B) muestran la vista ampliada de Rωxx (B) y esquemas de la configuración de medición (direcciones de B e I), respectivamente. (C) Rωxx y (D) R2ωxx por debajo de Tc0 (región de fluctuación superconductora, T =0,22 K e I =1 μA) en función del plano B perpendicular (rojo) o paralelo (azul) a I. En (A) a (D), Rωxx está normalizado por la resistencia de estado normal RN =128 ohmios, y Rωxx / R2ωxx está simétrizado / antisimetrizado en función de B. (E) Dependencia de la temperatura de γ =2R2ωxxRωxxBI en el estado normal (I =20 μA) y región de fluctuación superconductora (I =0,9 μA). Se extrajeron círculos púrpura (estado normal) y naranja (región de fluctuación superconductora) de la medición del escaneo del campo magnético de R2ωxx a un B bajo por debajo de 0.1 T, mientras que los puntos púrpura (estado normal) y naranja (región de fluctuación superconductora) se trazaron a partir del escaneo de temperatura de R2ωxx bajo B =3 y 0.05 T, respectivamente. Crédito:Science Advances, doi:10.1126 / sciadv.aay9120
Los científicos detallaron inicialmente la primera resistencia armónica (FHR) correspondiente a la resistencia lineal cerca de la transición superconductora para un voltaje de puerta de 5.0 V. Los resultados mostraron una dependencia de la temperatura en el límite de corriente baja (I =0.05 μA). Luego se enfocaron en la resistencia del segundo armónico (SHR) y acreditaron el transporte de carga no recíproco observado en la superficie de SrTiO 3 a la simetría polar dentro de la región de fluctuación superconductora y en el estado normal. El equipo observó transporte magnético en SrTiO 2-D inducido por la puerta 3 dentro de un campo magnético (B) perpendicular a la corriente (I) para los estados normal y superconductor, con un transporte no recíproco mejorado en la región de fluctuación superconductora. Para comparar la magnitud de la no reciprocidad entre el estado normal y la región de fluctuación de superconductividad, calcularon el coeficiente de magnetorresistencia no recíproca (γ), que dependía de la temperatura dentro de las regiones.
Posteriormente, el equipo midió la dependencia de las señales del segundo armónico en la corriente (I), en el estado normal y en la región de fluctuación superconductora. En el estado normal el SHR mostró una dependencia casi lineal de la corriente. En la región de fluctuación de la superconductividad en un campo magnético de 0,1 Tesla, el SHR aumentó linealmente, alcanzó un máximo de alrededor de 1 µA y se suprimió, para indicar la supresión de la superconductividad por la alta corriente.
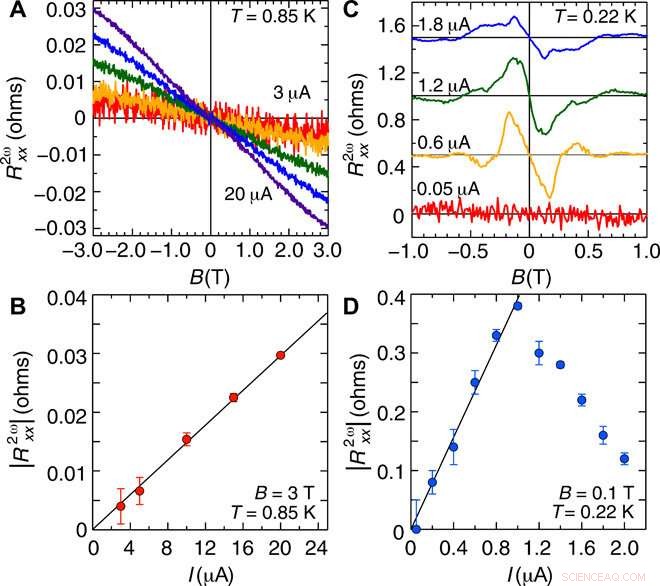
Dependencia actual de la magnetorresistencia del segundo armónico en la región de fluctuación normal y superconductora. (A) Magnetorresistencia de segundo armónico R2ωxx en T =0.85 K bajo I =3 μA (rojo), 5 μA (naranja), 10 μA (verde), 15 μA (azul), y 20 μA (violeta). R2ωxx está antisimetrizado en función de B. (B) ∣∣R2ωxx∣∣ en B =3 T como función de I, que se extrae de (A). La línea continua negra muestra un ajuste lineal en función de I. (C) Dependencia del campo magnético de ∣∣R2ωxx∣∣ en T =0.22 K bajo I =0.05 μA (rojo), 0,6 μA (naranja), 1,2 μA (verde), y 1,8 μA (azul). Cada curva se desplaza verticalmente en 0,5 ohmios y se antisimetriza en función de B. (D) Dependencia actual de ∣∣R2ωxx∣∣ en B =0,1 T, donde R2ωxx se considera una función lineal de B. En la región de baja corriente (I ≤ 1 μA), ∣∣R2ωxx∣∣ aumenta linealmente (línea negra sólida) con I. Crédito:Science Advances, doi:10.1126 / sciadv.aay9120
Para investigar más a fondo el posible origen del transporte superconductor no recíproco en el sistema, los científicos midieron la dependencia de la temperatura de FHR y SHR durante la transición. Para lograr esto, observaron la dependencia del campo magnético de FHR y SHR a varias temperaturas y observaron específicamente que SHR se mejoraba en gran medida durante el transporte superconductor. Aunque Itahashi et al. aplicó una corriente relativamente grande y un campo magnético en el plano, registraron un estado de resistencia cero a la temperatura más baja. Los resultados implicaron la existencia de la transición Berenzinskii-Kosterlitz-Thouless (transición BKT), el nombre de un equipo de físicos de materia condensada ganadores del premio Nobel. Describe las transiciones de fase en sistemas 2-D en la física de la materia condensada aproximadas por un modelo XY para comprender fases o estados inusuales de la materia en superconductores.
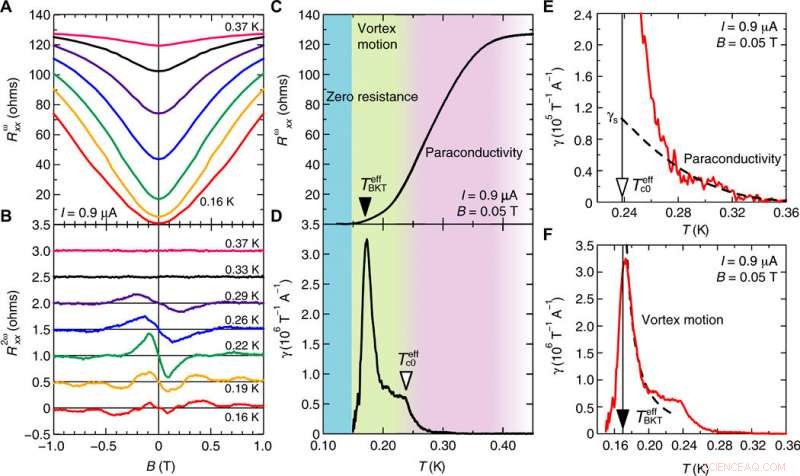
Dependencia de la temperatura de la magnetorresistencia y el transporte no recíproco. Dependencia del campo magnético de (A) la primera (Rωxx) y (B) la segunda magnetorresistencia armónica (R2ωxx) en T =0.16 K (rojo), 0,19 K (naranja), 0,22 K (verde), 0,26 K (azul), 0,29 K (violeta), 0,33 K (negro), y 0,37 K (rosa), respectivamente. En (B), cada curva se desplaza verticalmente 0,5 ohmios. Rωxx / R2ωxx está simétrizado / antisimetrizado en función de B. Variación de temperatura de (C) Rωxx y (D) γ bajo B =0,05 T e I =0,9 μA. En esta región, R2ωxx es lineal en función de B e I. Rωxx / γ está simétrizado / antisimetrizado en función de B. La estructura característica (estructura de torsión alrededor de T =0,24 K y estructura de pico alrededor de T =0,17 K) aparece en (D), según el cual podemos identificar dos regiones del transporte no recíproco de diferentes orígenes, es decir., región de paraconductividad y región de vórtice. A la temperatura más baja, se observa un estado de resistencia cero, donde Rωxx y γ se vuelven insignificantes. Ampliación de γ en la región de paraconductividad (E) y la región de vórtice (F). La línea punteada negra en (E) muestra la curva de ajuste por γ (T) =γs (1 − R (T) RN) 2, y la línea punteada negra en (F) indica la curva de ajuste por γ (T) =C (T − TeffBKT) −3/2. La resistencia en estado normal RN =128 ohmios se define como Rωxx en T =1.0 K. Crédito:Science Advances, doi:10.1126 / sciadv.aay9120
De este modo, Yuki M. Itahashi y sus colegas propusieron el transporte no recíproco en superconductores bidimensionales no centrífugos (sin simetría de inversión) dentro de un campo magnético. El transporte no recíproco se originó a partir de la fluctuación de amplitud del estado normal al superconductor. La dependencia de la temperatura del coeficiente de magnetorresistencia no recíproca (γ) observado en los experimentos concordaba bien con la imagen teórica microscópica del movimiento libre para vórtices y antivortices térmicamente excitados en superconductores 2-D polares. La respuesta no recíproca es, por tanto, una herramienta poderosa para comprender la naturaleza de los superconductores nocentrosimétricos.
Itahashi y col. creen que el transporte no recíproco podría aparecer universalmente para diferentes materiales en sistemas superconductores interfaciales con simetría polar. Los resultados proporcionan información sobre funciones previamente desconocidas de la superconductividad e información importante sobre el estado electrónico y los mecanismos de emparejamiento en superconductores nocentrosimétricos, como un tema importante para una mayor investigación. El trabajo destacó el transporte no recíproco en sistemas superconductores interfaciales como el superconductor 2-D inducido por puerta SrTiO 3 . El equipo probó el marcado salto del transporte no recíproco desde los estados normales a los superconductores como evidencia directa de una mejora gigante del transporte no recíproco en el sistema. Los resultados ofrecen información importante sobre los superconductores polares y allanan una nueva forma de buscar propiedades y funcionalidades emergentes desconocidas hasta ahora en interfaces y superconductores de óxido 2-D.
© 2020 Science X Network