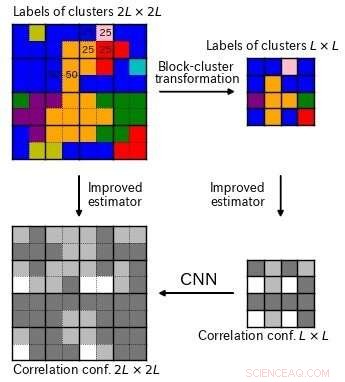
Una configuración de correlación (arriba a la izquierda) se reduce mediante una transformación de clúster de bloques recientemente desarrollada (arriba a la derecha). Tanto la configuración original como la reducida tienen una técnica de estimador mejorada aplicada para dar pares de configuración de diferente tamaño (fila inferior). Usando estos pares de entrenamiento, una CNN puede aprender a convertir patrones pequeños en grandes, logrando una transformación RG inversa exitosa. Crédito:Universidad Metropolitana de Tokio
Investigadores de la Universidad Metropolitana de Tokio han mejorado las técnicas de aprendizaje automático de "superresolución" para estudiar las transiciones de fase. Identificaron características clave de cómo grandes matrices de partículas que interactúan se comportan a diferentes temperaturas simulando matrices diminutas antes de usar una red neuronal convolucional para generar una buena estimación de cómo se vería una matriz más grande usando configuraciones de correlación. El enorme ahorro en costos computacionales puede dar lugar a formas únicas de comprender cómo se comportan los materiales.
Estamos rodeados de diferentes estados o fases de la materia, es decir, gases, líquidos y sólidos. El estudio de las transiciones de fase, cómo una fase se transforma en otra, se encuentra en el corazón de nuestra comprensión de la materia en el universo, y sigue siendo un tema candente para los físicos. En particular, la idea de universalidad, en el que materiales tremendamente diferentes se comportan de manera similar gracias a algunas características compartidas, es poderoso. Es por eso que los físicos estudian sistemas modelo, a menudo, cuadrículas simples de partículas en una matriz que interactúan a través de reglas simples. Estos modelos destilan la esencia de la física común compartida por los materiales y, Asombrosamente, todavía exhiben muchas de las propiedades de los materiales reales, como las transiciones de fase. Debido a su elegante sencillez, estas reglas se pueden codificar en simulaciones que nos dicen cómo se ven los materiales en diferentes condiciones.
Sin embargo, como todas las simulaciones, el problema comienza cuando queremos mirar muchas partículas al mismo tiempo. El tiempo de cálculo requerido se vuelve particularmente prohibitivo cerca de las transiciones de fase, donde la dinámica se ralentiza, y la longitud de la correlación, una medida de cómo el estado de un átomo se relaciona con el estado de otro a cierta distancia, crece más y más. Este es un dilema real si queremos aplicar estos hallazgos al mundo real:los materiales reales generalmente siempre contienen muchos más órdenes de magnitud de átomos y moléculas que la materia simulada.
Es por eso que un equipo dirigido por los profesores Yutaka Okabe e Hiroyuki Mori de la Universidad Metropolitana de Tokio, en colaboración con investigadores del Instituto de Tecnología y Bioinformática Shibaura de Singapur, han estado estudiando cómo extrapolar de manera confiable simulaciones más pequeñas a otras más grandes utilizando un concepto conocido como grupo de renormalización inversa (RG). El grupo de renormalización es un concepto fundamental en la comprensión de las transiciones de fase y llevó a Wilson a recibir el Premio Nobel de Física de 1982. Recientemente, el campo conoció a un poderoso aliado en las redes neuronales convolucionales (CNN), la misma herramienta de aprendizaje automático que ayuda a la visión por computadora a identificar objetos y descifrar la escritura a mano. La idea sería darle a un algoritmo el estado de una pequeña matriz de partículas y hacer que calcule cómo se vería una matriz más grande. Existe una fuerte analogía con la idea de imágenes de superresolución, donde blocky, Las imágenes pixeladas se utilizan para generar imágenes más suaves a una resolución más alta.
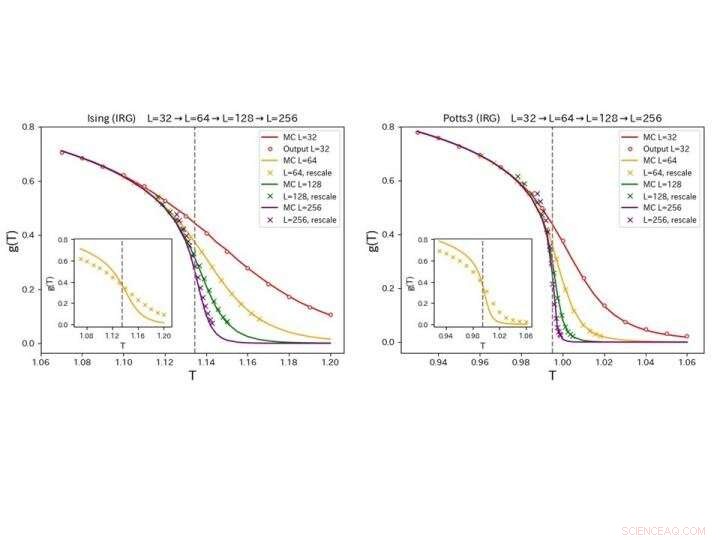
Las CNN capacitadas reproducen fielmente las tendencias encontradas a partir de simulaciones de sistemas más grandes para los modelos de Ising (izquierda) y Potts de tres estados (derecha). (recuadro) El reajuste de temperatura correcto se logra utilizando datos en algún tamaño de sistema arbitrario. Crédito:Universidad Metropolitana de Tokio
El equipo ha estado analizando cómo se aplica esto a los modelos de espín de la materia, donde las partículas interactúan con otras partículas cercanas a través de la dirección de sus giros. Los intentos anteriores han tenido problemas para aplicar esto a sistemas a temperaturas superiores a una transición de fase, donde las configuraciones tienden a parecer más aleatorias. Ahora, en lugar de usar configuraciones de giro, es decir, instantáneas simples de la dirección en la que apuntan los giros de las partículas, consideraron configuraciones de correlación, donde cada partícula se caracteriza por lo similar que es su propio giro al de otras partículas, específicamente los que están muy lejos. Resulta que las configuraciones de correlación contienen colas más sutiles sobre cómo se organizan las partículas, particularmente a temperaturas más altas.
Como todas las técnicas de aprendizaje automático, la clave es poder generar un conjunto de entrenamiento confiable. El equipo desarrolló un nuevo algoritmo llamado transformación de bloque-clúster para configuraciones de correlación para reducirlas a patrones más pequeños. Aplicar una técnica de estimador mejorada tanto a los patrones originales como a los reducidos, tenían pares de configuraciones de diferente tamaño basadas en la misma información. Todo lo que queda es entrenar a la CNN para convertir los patrones pequeños en patrones más grandes.
El grupo consideró dos sistemas, el modelo de Ising 2D y el modelo de Potts de tres estados, Ambos puntos de referencia clave para estudios de materia condensada. Para ambos, descubrieron que su CNN podía usar una simulación de un conjunto muy pequeño de puntos para reproducir cómo cambiaba una medida de la correlación g (T) a través de un punto de transición de fase en sistemas mucho más grandes. Comparando con simulaciones directas de sistemas más grandes, se reprodujeron las mismas tendencias para ambos sistemas, combinado con un simple cambio de escala de temperatura basado en datos en un tamaño de sistema arbitrario.
Una implementación exitosa de transformaciones RG inversas promete dar a los científicos un vistazo de tamaños de sistemas previamente inaccesibles. y ayudar a los físicos a comprender las características de los materiales a mayor escala. El equipo ahora espera aplicar su método a otros modelos que pueden mapear características más complejas, como un rango continuo de giros, así como el estudio de sistemas cuánticos.