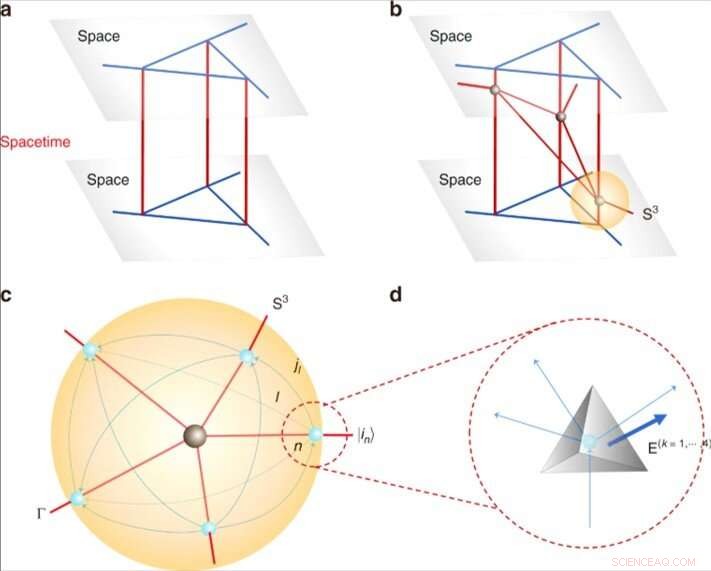
Espacio-tiempo cuántico y tetraedros. (a) Un espacio-tiempo cuántico estático 4d a partir de la evolución de la red de espines. (b) Un espacio-tiempo cuántico dinámico con un número de cinco vértices de valencia (en negro) mediante la intersección de las hojas del mundo, uno de los cuales se denota por S3. (c) La estructura local de un vértice de b considerando una S3 de 3 esferas que encierra el vértice. Las intersecciones entre las hojas del mundo y S3 dan una red de giro (en azul). Cada red de espín representa un estado | in⟩ y cada enlace l está orientado, que lleva un jl medio entero. (d) Tetraedros geométricos cuánticos. Cada nodo de la red de espines representa un tetraedro cuántico. Conectar 2 nodos por un enlace en la red de espín corresponde a pegar 2 tetraedros a través de la cara dual al enlace. Las áreas orientadas se denotan con E (k =1, ⋯, 4) =(E (k) x, E (k) y, E (k) z). Crédito:Física de la comunicación, doi:10.1038 / s42005-019-0218-5
La simulación cuántica juega un papel insustituible en diversos campos, más allá del alcance de las computadoras clásicas. En un estudio reciente, Keren Li y un equipo de investigación interdisciplinario en el Centro de Computación Cuántica, Ciencia e Ingeniería Cuántica y el Departamento de Física y Astronomía en China, Estados Unidos, Alemania y Canadá. Estados de red de espines simulados experimentalmente mediante la simulación de tetraedros del espacio-tiempo cuántico en un simulador cuántico de resonancia magnética nuclear (RMN) de cuatro qubits. La fidelidad experimental fue superior al 95 por ciento. El equipo de investigación utilizó los tetraedros cuánticos preparados por resonancia magnética nuclear para simular una amplitud (modelo) de vértice de espuma de espín bidimensional (2-D), y mostrar la dinámica local del espacio-tiempo cuántico. Li y col. midió las propiedades geométricas de los tetraedros cuánticos correspondientes para simular sus interacciones. El trabajo experimental es un intento inicial y un módulo básico para representar el vértice del diagrama de Feynman en la formulación de spinfoam, estudiar la gravedad cuántica de bucles (LQG) mediante el procesamiento de información cuántica. Los resultados ya están disponibles en Física de la comunicación.
Las computadoras clásicas no pueden estudiar grandes sistemas cuánticos a pesar de las exitosas simulaciones de una variedad de sistemas físicos. Las restricciones sistemáticas de las computadoras clásicas ocurrieron cuando el crecimiento lineal de los tamaños de los sistemas cuánticos correspondió al crecimiento exponencial del Espacio de Hilbert, una base matemática de la mecánica cuántica. Los físicos cuánticos tienen como objetivo superar el problema utilizando computadoras cuánticas que procesan la información de forma intrínseca o cuántica para superar exponencialmente a sus homólogos clásicos. En 1982, El físico Richard Feynman definió las computadoras cuánticas como sistemas cuánticos que pueden controlarse para imitar o simular el comportamiento o las propiedades de sistemas cuánticos relativamente menos accesibles.
En el presente trabajo, Li y col. utilizó resonancia magnética nuclear (RMN) con un alto rendimiento controlable en el sistema cuántico para desarrollar métodos de simulación. La estrategia facilitó la presentación de geometrías cuánticas del espacio y el espacio-tiempo basadas en las analogías entre los estados de espín nuclear en muestras de RMN y los estados de redes de espín en la gravedad cuántica. La gravedad cuántica tiene como objetivo unir la gravedad de Einstein con la mecánica cuántica para ampliar nuestra comprensión de la gravedad a la escala de Planck (1,22 x 10 19 GeV). En la escala de Planck (magnitudes del espacio, tiempo y energía) La gravedad de Einstein y el continuo de la ruptura del espacio-tiempo se pueden reemplazar a través del espacio-tiempo cuántico. Los enfoques de investigación para comprender los espaciotiempos cuánticos se basan actualmente en redes de espín (un gráfico de líneas y nodos para representar el estado cuántico del espacio en un determinado momento), que son importantes marco no perturbativo de la gravedad cuántica.
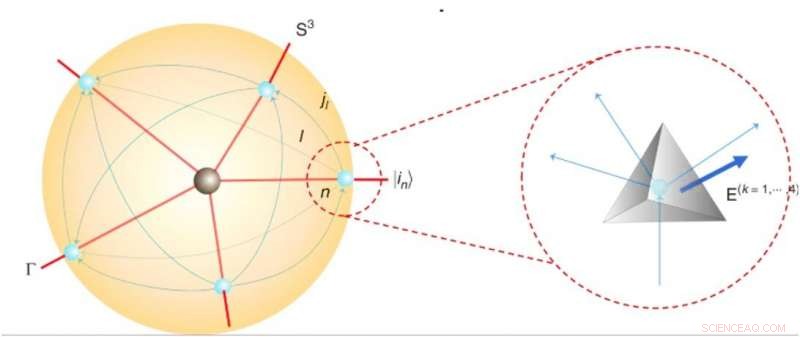
El espacio-tiempo cuántico y los tetraedros dentro de una red de espines. Crédito:Física de la comunicación, doi:10.1038 / s42005-019-0218-5
En 1971, El físico Roger Penrose propuso redes de espín motivadas por la teoría de twistor con aplicaciones posteriores a la gravedad cuántica de bucles (LQG). Las redes de espín eran estados cuánticos que representan geometrías cuánticas del espacio fundamentalmente discretas en la escala de Planck. En el presente estudio, el equipo de investigación representó la red de espín mediante un gráfico con enlaces y nodos coloreados por mitades de espín. Por ejemplo, cualquier nodo con aristas correspondía a una geometría y, por tanto, un gráfico que contenía nodos cuatrivalentes correspondía a la geometría tetraedro cuántica.
El equipo de investigación desarrolló una "red" que contiene una serie de láminas del mundo tridimensionales (3-D) (superficies 2-D) y sus intersecciones. Demostraron que cada vértice donde se unían las superficies, condujo a una transición cuántica que cambió la red de espín para representar la dinámica local de la geometría cuántica. Al igual que los diagramas de Feynman (representaciones esquemáticas de expresiones matemáticas que describen el comportamiento de partículas subatómicas), los espaciotiempos cuánticos codificaron las amplitudes de transición y las amplitudes de la espuma de espín entre las redes de espín inicial y final. Los espaciotiempos cuánticos y las amplitudes de la espuma de espín desarrolladas en el estudio proporcionaron un enfoque consistente y prometedor de la gravedad cuántica. Li y col. presentó la simulación de RMN por la capacidad de controlar qubits individuales con alta precisión. Los tetraedros cuánticos y las amplitudes de los vértices sirvieron como bloques de construcción de LQG (gravedad cuántica de bucle) para abrir una nueva ventana para incluir LQG en experimentos cuánticos.
Los científicos primero derivaron ecuaciones para describir un tetraedro cuántico dentro de una red de espines. En un modelo de espacio-tiempo cuántico dinámico esquemático de 3 + 1 dimensiones, demostraron que un átomo es una esfera tridimensional que encierra una parte del espacio-tiempo cuántico que rodea a un vértice. El equipo modeló el límite del espacio-tiempo cuántico cerrado precisamente como una red de espín y mostró la posibilidad de simular grandes espaciotiempos cuánticos con muchos vértices pegando cuánticamente los átomos. La estructura resultante se asemejaba a la amplitud del vértice del espacio-tiempo cuántico similar a los modelos de celosía topológica desarrollados previamente por Ooguri en cuatro dimensiones. Los investigadores mostraron a LQG para identificar geometrías cuánticas de tetraedros con los momentos angulares cuánticos. La identificación les permitió simular geometrías cuánticas con registros cuánticos (análogo mecánico cuántico de un registro de procesador clásico). En general, un registro cuántico se puede lograr matemáticamente utilizando productos tensoriales.
ARRIBA:Estados preparados experimentalmente en la esfera de Bloch y sus correspondientes tetraedros clásicos. Los estados toman la forma cosθ2 | 0⟩L + eiϕsinθ2 | 1⟩L y están etiquetados por Ai, Bi, Ci, Di, Ei (i =0, 1), dentro de los cuales, C0 y C1 son tetraedros regulares. | 0L⟩ y | 1L⟩ son los estados base en un subespacio de un sistema de cuatro qubit, representando un solo qubit lógico. INFERIOR:Valores de coseno de ángulos entre caras normales en el tetraedro cuántico (los cosenos de ángulos diedros difieren por un signo menos). Los resultados de los experimentos (teoría) están representados por las columnas de colores (transparentes). Las barras de error provienen de la incertidumbre al ajustar los espectros de resonancia magnética nuclear (RMN). Crédito:Física de la comunicación, doi:10.1038 / s42005-019-0218-5 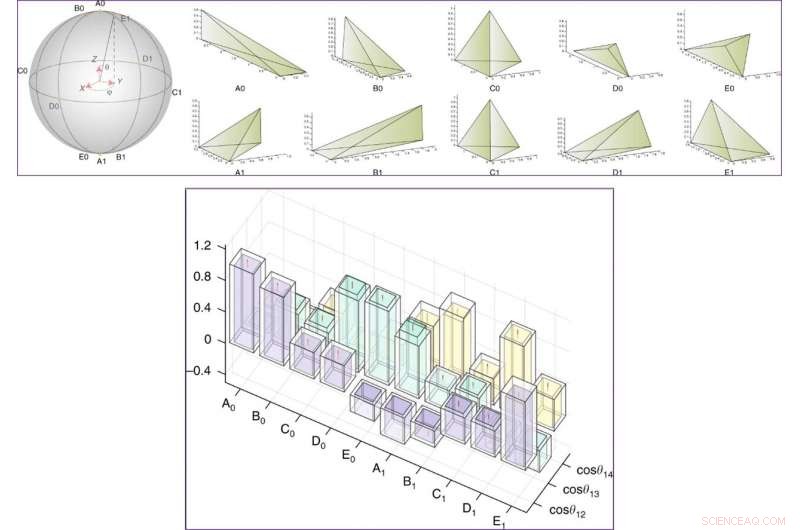
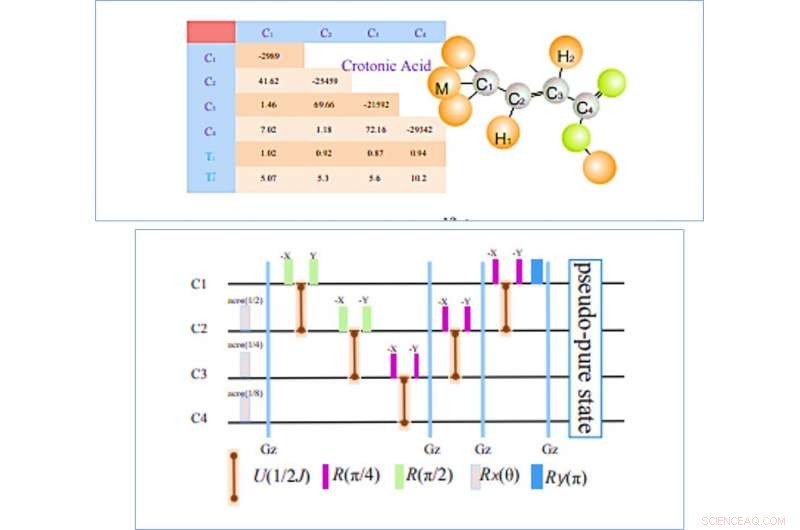
IZQUIERDA:Estructura de la molécula de ácido crotónico; Los cuatro núcleos de 13C se indican como los cuatro qubits y la tabla de la izquierda presenta los parámetros que construyen el hamiltoniano interno. Desplazamientos químicos (Hz), Las fuerzas de acoplamiento J (Hz) y los tiempos de relajación (T1 y T2) se enumeran en la parte diagonal, elementos fuera de la diagonal y la parte inferior, respectivamente. Todos los parámetros se midieron en un espectrómetro Bruker DRX de 700 MHz a temperatura ambiente. DERECHA:Secuencias de pulsos para crear el estado pseudo-puro. Basado en la técnica de promedio espacial, los circuitos incluyen operaciones locales, cinco evoluciones de acoplamiento en J, y cuatro pulsos de gradiente z para destruir los términos coherentes no deseados. la duración de la evolución libre de 1 / 2J depende de la fuerza del acoplamiento J entre los giros relevantes. Crédito:Física de la comunicación, doi:10.1038 / s42005-019-0218-5
Para obtener las amplitudes de los vértices, los investigadores calcularon los productos internos entre cinco estados cuánticos tetraédricos diferentes. Idealmente, los investigadores podrían haber usado una computadora cuántica de 20 qubit, estableciendo estados de dos qubit entrelazados al máximo entre dos tetraedros arbitrarios. Sin embargo, Dado que una computadora cuántica de tales dimensiones está actualmente más allá de la tecnología de vanguardia comercializada, los investigadores realizaron alternativamente una tomografía completa de la preparación del estado para obtener información de los estados cuánticos del tetraedro. Cuando los científicos calcularon las fidelidades entre los estados experimentales del tetraedro cuántico y la teoría, los resultados estuvieron muy por encima del 95 por ciento. Usando los tetraedros cuánticos, el equipo de investigación simuló la amplitud del vértice. Compararon los resultados entre el experimento y la simulación numérica entre los cinco tetraedros. Respectivamente, Los puntos de silla de la amplitud en los experimentos ocurrieron donde los cinco tetraedros interactuantes demostraron un significado geométrico simple cuando se pegaron para formar un cuatro simplex geométrico.
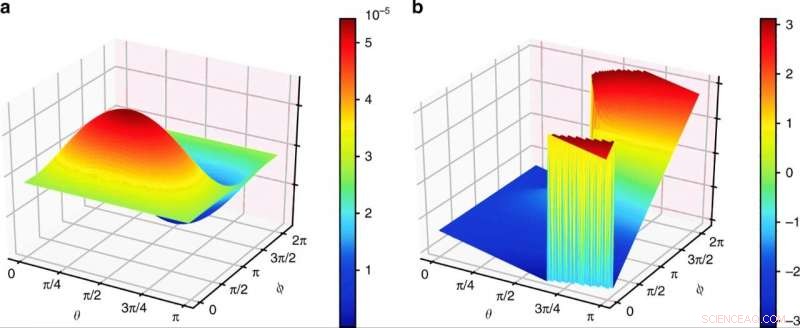
Los resultados de las amplitudes de vértice simuladas a son la amplitud de la ecuación. (3) yb describen la información de su fase. θ y ϕ son los parámetros del estado del tensor invariante de cuatro qubit correspondientes a las coordenadas esféricas en la esfera de Bloch. Crédito:Física de la comunicación, doi:10.1038 / s42005-019-0218-5
De este modo, Keren Li y sus colaboradores utilizaron un registro cuántico en el sistema de RMN para crear 10 estados de tensor invariante para representar 10 tetraedros cuánticos. Alcanzaron una fidelidad superior al 95 por ciento y posteriormente midieron los ángulos diedros (dos caras planas) del modelo. Consideraron los errores de ajuste del espectro y la identificación geométrica para comprender el éxito en la simulación de tetraedros cuánticos en el estudio. El nuevo trabajo de investigación presentó un primer paso para explorar los estados de la red de espín y las amplitudes de la espuma de espín utilizando un simulador cuántico. El trabajo adjunto también demostró experimentos válidos para estudiar LGQ.
© 2019 Science X Network