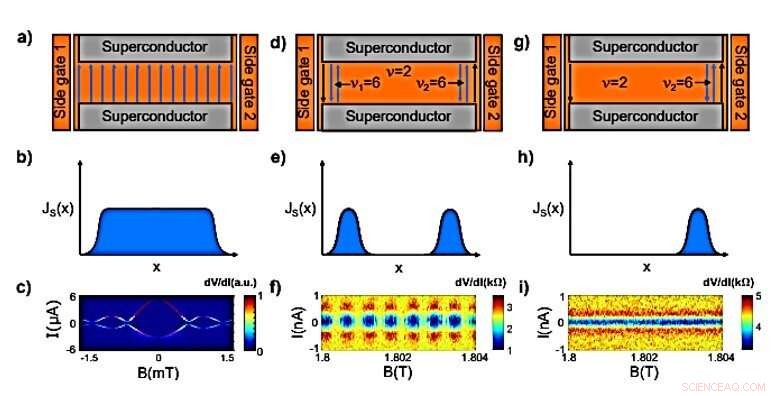
Comparación de tres columnas de las distribuciones de supercorriente y los patrones de interferencia magnética resultantes. a) Diagrama de flujo de supercorriente en campos magnéticos bajos, resultando en una distribución uniforme que se muestra en el panel (b). c) Medición del segundo dispositivo con un campo magnético bajo que muestra un patrón de interferencia típico de Fraunhofer con un período de ∼ 0,7 mT, lo que indica una distribución uniforme de supercorriente. Los datos son una derivada numérica de las curvas I-V medidas (unidades arbitrarias). T =230 mK. d) Esquema de los bordes QH cuando se aplican ambas puertas laterales (volumen ν =2, inducida localmente ν =6 en cada borde). Los estados de contrapropagación estrechamente espaciados soportan supercorrientes en ambos bordes de la muestra, resultando en la distribución que se muestra en el panel (e). El panel (f) muestra el patrón de interferencia magnética similar a SQUID (dispositivo superconductor de interferencia cuántica) de la supercorriente cuántica de Hall correspondiente al panel (d) con una periodicidad de ∼ 0,6 mT. El panel (g) es similar al panel (d) pero con una sola puerta lateral aplicada. Esto da como resultado que la supercorriente fluya solo en un borde de la muestra, como se muestra en el panel (h). El panel (i) muestra el patrón de interferencia magnética correspondiente al panel (g). No hay variación en el patrón en esta escala de campo, indicando un solo, Distribución de corriente muy localizada. Crédito:Science Advances, doi:10.1126 / sciadv.aaw8693
En un informe reciente publicado en Avances de la ciencia , Andrew Seredinski y sus colaboradores presentaron una unión Josephson basada en grafeno con puertas laterales dedicadas fabricadas con la misma hoja de grafeno que la unión en sí. El equipo de investigación interdisciplinario en los departamentos de física, La astronomía y los materiales avanzados en los EE. UU. y Japón encontraron que las puertas laterales eran altamente eficientes, permitiéndoles controlar la densidad del portador a lo largo de cualquier borde de la unión a través de una amplia gama de campos magnéticos. Por ejemplo, poblaron el siguiente nivel de Landau (donde el número de electrones es directamente proporcional a la fuerza del campo magnético aplicado) dentro de campos magnéticos en el rango de 1 a 2-Tesla (T), para dar lugar a mesetas de Hall cuánticas. Luego, cuando introdujeron estados de borde de Hall cuánticos contrapropagados a ambos lados del dispositivo, observaron una supercorriente localizada a lo largo del borde del cruce. En el presente trabajo, estudiaron estas supercorrientes en función del campo magnético y la densidad de portadores.
En mecánica cuántica, los físicos clasifican las partículas como fermiones o bosones. Esta clasificación es crucial para comprender una variedad de sistemas físicos, incluidos los láseres, metales y superconductores. Las interacciones entre electrones o átomos en algunos sistemas bidimensionales (2-D) pueden conducir a la formación de cuasi partículas que rompen con la dicotomía fermión-bosón; para formar estados de materia "no abelianos". Muchos estudios experimentales intentan identificar estados no abelianos en sistemas que manifiestan los efectos de Hall cuántico (QH) (cuantificación de la resistencia en sistemas electrónicos bidimensionales). La identificación de tales estados será útil para la computación cuántica.
Los físicos predicen la interacción de los estados espín-helicoidales y la superconductividad para permitir el acceso a excitaciones no abelianas como los modos Majorana Zero (MZM). Estos estados pueden formar la base de las arquitecturas de computación cuántica, que aprovechan las protecciones topológicas para lograr la tolerancia a fallas, lo que permite que un sistema continúe funcionando correctamente en caso de falla. Los investigadores tienen como objetivo desarrollar varias técnicas, incluyendo nanocables híbridos superconductores-semiconductores y estructuras de aisladores superconductores-topológicos para tales aplicaciones basadas en cuasipartículas. El interés de la investigación reciente en la superconductividad también había llevado a una ráfaga de actividad en la interfaz de la superconductividad y el efecto Hall cuántico (QH). Por ejemplo, Los científicos han deducido que los contactos superconductores cuasi unidimensionales (1-D) pueden habilitar MZM y parafermiones, mientras que las heteroestructuras de grafeno y nitruro de boro hexagonal (BN) con contactos superconductores 1-D pueden demostrar una notable transparencia de contacto para observar la supercorriente en el régimen QH. Sin embargo, Los detalles microscópicos de la supercorriente en el régimen QH siguen siendo hasta ahora un tema abierto.
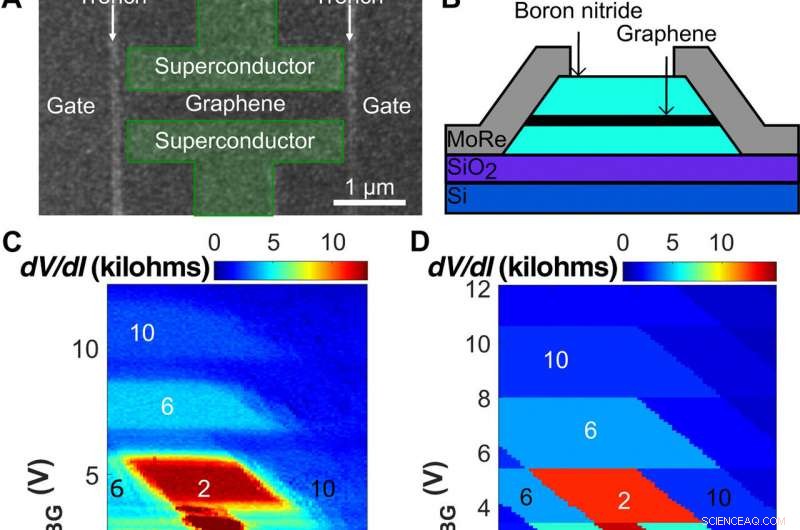
El diseño del dispositivo y la influencia de la puerta en las mesetas de QH. (A) Micrografía de microscopía electrónica de barrido (SEM) del dispositivo antes del grabado con iones reactivos. Los contactos más están delineados y de color verde para el contraste. Dos trincheras (gris claro), ~ 60 nm de ancho, separe el cruce de las puertas laterales. Los contactos de MoRe están separados de las trincheras por regiones de grafeno de ~ 100 nm de ancho, evitando el contacto directo entre MoRe y el borde de la mesa. (B) Vista lateral esquemática de una sección transversal vertical de (A). (C) Mapa de resistencia en función del voltaje de la puerta trasera, VBG, y voltajes de compuerta lateral aplicados simétricamente, VSG1 =VSG2, en B =1,8 T. Las regiones en forma de diamante corresponden a las mesetas de resistencia cuantificada. Sus límites horizontales (afectados solo por VBG) corresponden a una densidad de electrones constante en la masa. Los límites laterales inclinados de los diamantes corresponden a factores de relleno constantes cerca de los bordes, donde las influencias de las puertas traseras y laterales se compensan entre sí. Los números blancos marcan el factor de llenado de la muestra, mientras que los números negros en la puerta del lado alto marcan la conductancia de la muestra en unidades de e2 / h. (D) Simulación electrostática de elementos finitos de (C) que reproduce las regiones en forma de diamante de conductancia constante. Las mesetas de conductancia marcadas en (C) están marcadas de manera similar. (E) Resistencia de la muestra en función de VBG en varios VSG1, 2, correspondiente a las secciones transversales verticales de (C). Las curvas muestran que las mesetas QH se desarrollan mejor con las puertas laterales configuradas en −1 V.En VSG1, 2 =- 3 V y +1 V, las mesetas se encogen y se vuelven asimétricas entre el electrón y los lados dopados con huecos, como se encuentra a menudo en muestras sin control de puerta lateral. Crédito:Science Advances, doi:10.1126 / sciadv.aaw8693
En el presente trabajo, Seredinski y col. examinó una unión de Josephson de grafeno con dos puertas laterales de grafeno para manipular directamente los estados del borde QH. Sintonizaron cada puerta para cambiar el factor de llenado del nivel de Landau a lo largo de los bordes para observar una supercorriente, únicamente localizado a lo largo de un borde. El equipo construyó las muestras a partir de grafeno encapsulado en nitruro de boro hexagonal (BN) para proteger los dispositivos de la contaminación y producir transporte balístico a través de escalas micrométricas. Grabaron la pila de grafeno-BN y luego fabricaron contactos cuasi-1-D en la región expuesta. Usaron molibdeno renio (MoRe), un superconductor de tipo II y separó los contactos de 3 μm de ancho por 500 nm para formar la configuración experimental. En el siguiente paso, formaron tanto la unión como las puertas laterales grabando trincheras estrechas a cada lado de los contactos, para controlar eficientemente la densidad de electrones a lo largo de los bordes de la unión, después de aplicar voltaje a las regiones de grafeno. No superpusieron las trincheras grabadas con los contactos y en su lugar los espaciaron usando una tira de grafeno, para evitar que los electrones formen un túnel directamente desde el superconductor hasta el borde.
Cuando Seredinksi et al. aplicó un campo magnético perpendicular a la muestra, la unión entró en el régimen QH (Quantum Hall). Por 1.8 Tesla, el efecto QH fue muy bien desarrollado y observado usando mapas de resistencia reproducidos por una simple simulación electrostática en el trabajo. El equipo de investigación obtuvo más información sobre la función del dispositivo al aplicar las puertas laterales de forma independiente. Observaron la influencia de las puertas laterales en las conductancias para mostrar una diafonía insignificante entre la puerta izquierda y el borde derecho. y viceversa. Los científicos ajustaron las puertas para inducir un estado QH para crear estados de contrapropagación dentro del dispositivo. El equipo observó la supercorriente QH y sus patrones de interferencia como una región de resistencia suprimida flanqueada por picos; característica de una pequeña supercorriente. El equipo reguló las características del dispositivo para localizar la supercorriente en cualquiera de las uniones.
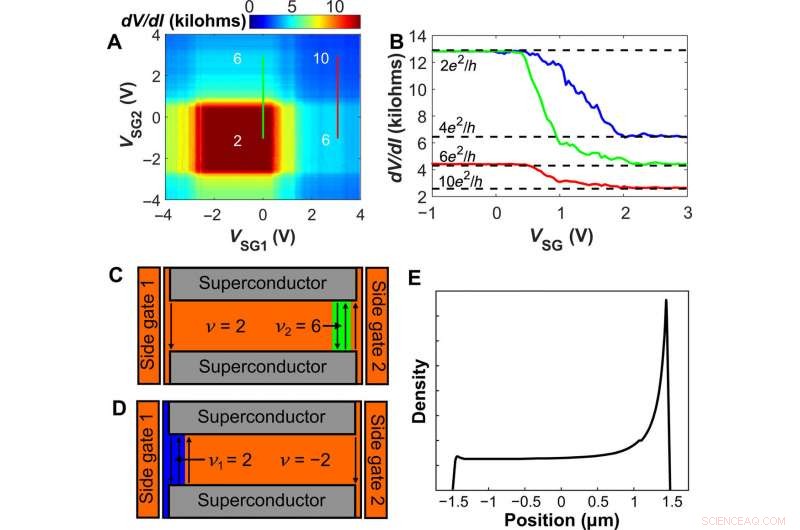
Mesetas de QH inducidas por la puerta lateral. (A) Mapa dV / dI trazado frente a los voltajes de puerta lateral VSG1 y VSG2 en B =1.8 T. El voltaje de puerta trasera se fija en VBG =4.7 V, correspondiente al estado global ν =2. Los números marcan la conductancia de la muestra en unidades de e2 / h. (B) Resistencia de la muestra medida en función de una puerta lateral única. Las curvas verde y roja corresponden a las líneas verticales en (A) en VSG1 =0 y 3 V, respectivamente (con VBG =4,7 V). La curva azul muestra una traza similar con un factor de llenado a granel ν =- 2 (VBG =1.5 V), barriendo VSG1 con VSG2 =0 V. (C y D) Esquemas correspondientes a las curvas verde y azul en (B) para VSG mayor que ∼2 V. Se crean canales de borde adicionales cerca de la puerta, con factor de llenado local ν2 =6 (C, región verde) y ν1 =2 (D, región azul). La conductancia adicional es igual a 4e2 / hy 2e2 / h en (C) y (D), respectivamente, además de la conductancia base de 2e2 / h, como se observa para las curvas azul y verde en (B). (E) Esquema de la densidad de portadores dentro de la unión de grafeno en función de la posición cuando SG2 (1) está activo (pasivo), similar a (C). Crédito:Science Advances, doi:10.1126 / sciadv.aaw8693.
La supercorriente no varió para pequeños cambios en el campo magnético. Por ejemplo, cuando el equipo abrió una puerta lateral, la distancia entre los canales de borde de contrapropagación en el dispositivo facilitó el acoplamiento de los estados de borde al superconductor, para que apareciera la supercorriente. Cuando aplicaron ambos lados de las puertas simultáneamente, la dependencia de la supercorriente de los campos magnéticos cambió por completo. El mapa resultante demostró un patrón de interferencia similar a un dispositivo de interferencia cuántica superconductor (SQUID). Cuando Seredinski et al. exploró el dispositivo como un interferómetro para supercorrientes QH, cambiaron el campo a 1 T para observar una firma de sobrealimentación más robusta. Obtuvieron el patrón de oscilaciones de resistencia en el campo magnético, donde el período de oscilaciones fue independiente del voltaje de la puerta, mientras que la fase de oscilaciones variaba con la puerta.
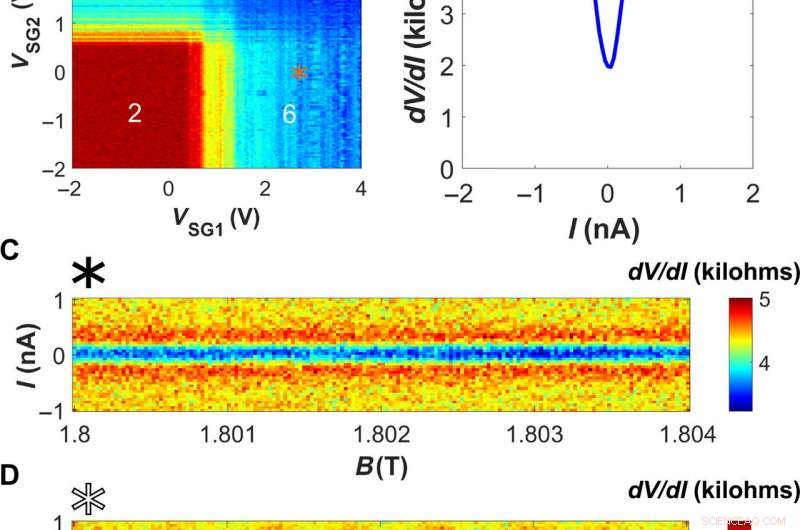
Supercorriente QH y sus patrones de interferencia. (A) Mapa de resistencia diferencial frente a VSG1, 2 como en la Fig.2A pero medido con polarización de corriente CC de 0 nA, permitiendo la observación de la resistencia suprimida debido a la supercorriente. Las ubicaciones de voltaje de puerta de (B) a (D) están marcadas por (B) un asterisco naranja, (C) un asterisco negro, y (D) un asterisco blanco. (B) dV / dI medido frente a I, lo que indica la presencia de una supercorriente en la parte superior de la meseta h / 6e2 cuantificada. (C) Mapa de campo magnético de corriente de la resistencia diferencial cuando se induce una supercorriente a lo largo de un lado de la muestra solo con VSG2, mientras que VSG1 permanece en cero. La supercorriente no es sensible a un cambio incremental de campo en una escala de pocos militesla. (D) Un mapa similar con ambas puertas laterales induciendo supercorriente, mostrando un patrón de interferencia similar a un CALAMAR. Crédito:Science Advances, doi:10.1126 / sciadv.aaw8693.
En un patrón de interferencia adicional, el equipo de investigación observó la diferencia en la resistencia de la muestra entre el sesgo de CC de 0 y 10 nanoamperios (nA), para resaltar las regiones superconductoras. Midieron el mapa en función de ambas puertas laterales y observaron la interferencia correspondiente a las supercorrientes que fluían a lo largo de la puerta lateral 1 (SG1) y la puerta lateral 2 (SG2). Las dos puertas presentaron una eficiencia comparable. Cuando los científicos aumentaron el voltaje de una puerta, disminuyeron el voltaje de la puerta opuesta para mantener aproximadamente la misma área del SQUID (dispositivo superconductor de interferencia cuántica). Estos cambios de área fueron suficientes para evolucionar la fase de diferencia a través de la unión, aunque demasiado pequeño para crear cambios notables en la periodicidad del campo magnético.
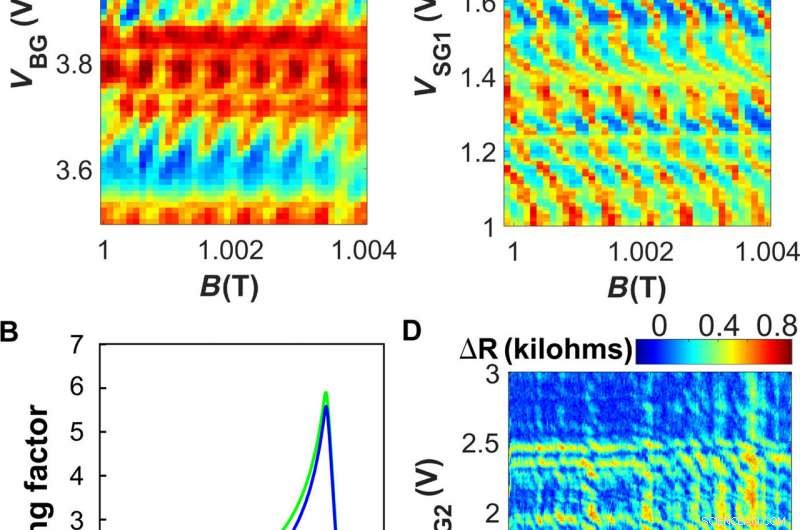
Interferometría de supercorriente QH. (A) Mapa dV / dI medido en VSG1 =2.34 V y VSG2 =2.36 V en función de VBG y B cerca de 1 T. Para un voltaje de puerta dado, las regiones de resistencia suprimida corresponden a una supercorriente más fuerte. La fase de las oscilaciones depende del voltaje de la puerta, indicando que el área de interferencia disminuye con el voltaje de la puerta (positivo dVBG / dB). Esto se explica porque los estados del borde interno se mueven más hacia adentro a medida que aumenta la densidad de electrones [esquema en (B)]. (B) Esquema de la densidad del portador en la muestra a lo largo de la línea media entre los contactos. La línea azul representa alguna densidad de carga de referencia; la línea verde muestra un voltaje de puerta trasera más alto. (C) Mapa dV / dI similar a (A) medido en función del voltaje B y SG1 para VBG =3.8 V. El mapa muestra un patrón de interferencia con una pendiente opuesta a la de (A), lo que indica que el área de interferencia aumenta con el voltaje de la puerta a medida que los electrones se empujan más hacia la puerta. (D) Mapa ΔR que muestra la diferencia entre la resistencia en las condiciones de polarización de CC de 0 y 10 nA, medido a 1 T con VBG =3,9 V. Ambos voltajes de compuerta lateral son lo suficientemente altos como para inducir una supercorriente (VSG1, 2> 1 V), y las características verticales y horizontales corresponden a la supercorriente inducida por SG1 o SG2, respectivamente. En sus intersecciones, aparecen características diagonales adicionales, indicando interferencia entre las supercorrientes en los dos lados de la muestra. Las franjas tienen una pendiente ∼ −1, sugiriendo una eficiencia comparable de las dos puertas laterales. Crédito:Science Advances, doi:10.1126 / sciadv.aaw8693.
De este modo, Andrew Seredinski y sus colegas demostraron que las puertas laterales de grafeno nativo son notablemente eficientes en el control de la propagación del estado de borde en el régimen de Hall cuántico (QH). Observaron supercorrientes inducidas por las puertas laterales, para ser transportado por los estados de borde QH. Estas supercorrientes fluían de forma independiente en cada borde del dispositivo y podían ser controladas de forma independiente por sus correspondientes puertas. El experimento abre una nueva ruta prometedora para acoplar superconductores con estados de borde QH para inducir excitaciones no abelianas para formar la base de las arquitecturas de computación cuántica.
© 2019 Science X Network