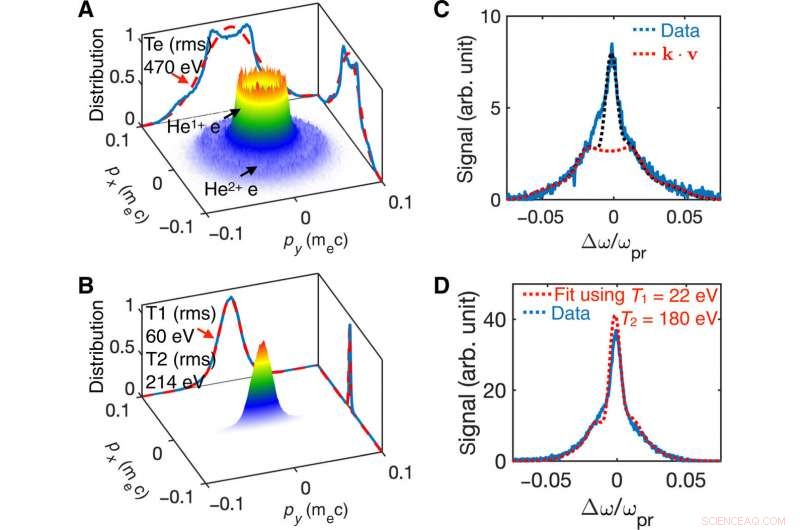
Distribución de velocidad de electrones inicial (EVD) del plasma de helio de ionización inducida por campo óptico (OFI). EVD (A) para polarización circular (CP) y (B) para pulso láser de polarización lineal (LP) de simulaciones 3D OSIRIS. Las líneas azules sólidas en (A) y (B) muestran las distribuciones proyectadas. En el caso CP (A), la distribución proyectada se desvía significativamente de una distribución maxwelliana que tiene la misma temperatura de raíz cuadrada media (rms) de 470 eV, como se muestra con la línea discontinua roja. En el caso LP (B), la distribución proyectada se puede aproximar bien mediante una distribución de dos temperaturas (1D Maxwelliana) con THe1 + =60eV y THe2 + =60eV =214 eV. Las líneas azules en (C) y (D) muestran el espectro de TS medido para CP (C) y LP (D) para una densidad plasmática inicialmente bastante baja de 6,6 × 1017 cm − 3. Las líneas punteadas rojas en (C) y (D) se ajustan al espectro medido. Crédito:Science Advances, doi:10.1126 / sciadv.aax4545
Las inestabilidades cinéticas comúnmente surgen de distribuciones de velocidad de electrones anisotrópicos (diferentes propiedades en diferentes direcciones) dentro de la ionosfera, plasmas cósmicos y terrestres. Pero solo unos pocos experimentos han validado esa teoría hasta ahora. Se pueden utilizar pulsos de láser ultrarrápidos durante la ionización de átomos por campo óptico para generar plasmas con distribuciones de velocidad de electrones anisotrópicos conocidas para comprender el fenómeno en la práctica. En un estudio reciente, Chaojie Zhang y un equipo de investigación interdisciplinario en los departamentos de Ingeniería Eléctrica e Informática, y Física y Astronomía en los EE. UU., mostró que el plasma se sometió a una filamentación de dos corrientes después de la ionización, pero antes de la termalización basada en la colisión de los electrones constituyentes.
Observaron inestabilidades de Weibel (presentes en plasma homogéneo o casi homogéneo) que isotropizan (propiedades similares en todas las direcciones) las distribuciones de electrones. Los investigadores midieron la frecuencia dependiente de la polarización y las tasas de crecimiento de estas inestabilidades cinéticas utilizando la dispersión de Thomson (TS) de un láser de sonda, que concuerda bien con la teoría cinética y las simulaciones. El equipo de investigación demostró una plataforma de laboratorio fácilmente desplegable para estudiar las inestabilidades cinéticas dentro del plasma; los resultados ahora se publican en Avances de la ciencia .
Los plasmas son susceptibles a inestabilidades cinéticas cuando la distribución de la velocidad de sus electrones plasmáticos constituyentes, iones o ambos se vuelven no térmicos. Los físicos pueden validar experimentalmente la teoría de estas inestabilidades si tienen conocimiento directo de las funciones de distribución de velocidad inicial de tales especies de plasma. Con el advenimiento del pulso ultracorto intenso, láseres de infrarrojo cercano, Los investigadores han ionizado átomos y / o moléculas de un gas en unos pocos ciclos de láser para generar funciones de distribución de velocidad de electrones (EVD) anisotrópicas o no térmicas. El proceso se conoce como ionización de túnel o inducida por campo óptico (OFI). La capacidad de iniciar funciones de distribución de velocidad permitirá a los investigadores probar cuantitativamente la teoría cinética de los plasmas en escalas de tiempo ultrarrápidas. antes de las colisiones electrón-electrón (e-e) y la termalización de iones. Sin embargo, los mecanismos y la escala de tiempo en los que los electrones del plasma evolucionaron de un estado anisotrópico a un estado térmico siguen siendo un problema experimental sin resolver en la ciencia básica.
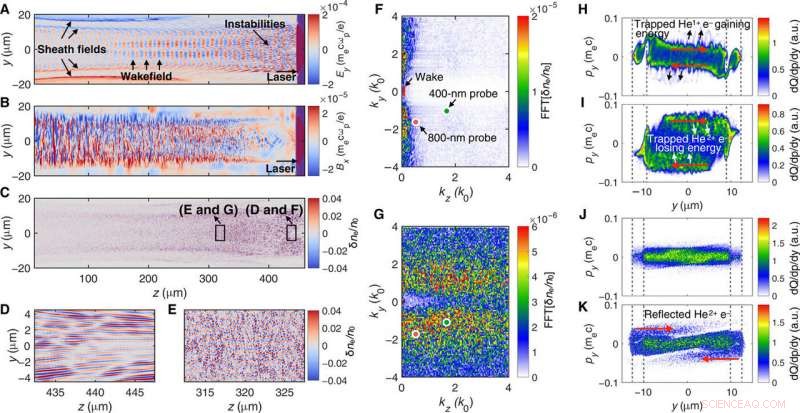
Las simulaciones 2-D muestran inestabilidades de filamentación y flujo cinético desencadenado por OFI en un plasma de helio. El plasma (ne =5 × 1018 cm − 3) es ionizado por un láser CP (τ =50 fs, w0 =8 micras, I =1,6 × 1017 W / cm2). El campo Ey, Campo Bx, y las fluctuaciones de densidad asociadas con la inestabilidad se muestran en (A), (B), y C), respectivamente. (D) y (E) se acercan a las regiones marcadas por los cuadros en (C). El espacio k correspondiente de estas fluctuaciones de densidad se muestra en (F) y (G), donde los dos puntos marcan la k de las ondas que se están midiendo en los experimentos y donde se utiliza la sonda de 400 nm (800 nm) para los pulsos de la bomba CP (LP). (H e I) y (J y K) muestran el espacio de fase transversal de los electrones He1 + y He2 + ionizados por láseres CP y LP, respectivamente. Estos resultados provienen de simulaciones con resoluciones más altas. Las barras de color representan la densidad de los electrones [en unidades arbitrarias (a.u.)]. La caja de simulación tiene 35 μm de ancho en y. Debido a que el láser solo ioniza los 20 μm centrales de He, En estos gráficos se muestra una ventana de 30 μm. En todos los casos, los electrones dentro de una placa Δz =2 μm en z =20 μm se utilizan para mostrar el espacio de fase. (H) e (I) se toman 0.14 ps mientras que (J) y (K) se toman 1.9 ps después de que el láser ha pasado la losa. Las líneas discontinuas grises marcan la ubicación de las delgadas fundas. La dirección de las flechas indica el cambio de las distribuciones de impulso. Crédito:Science Advances, doi:10.1126 / sciadv.aax4545
Como resultado de la gama extremadamente amplia de situaciones que dan lugar a inestabilidades cinéticas, incluidos los destellos de rayos gamma, plasmas de positrones de electrones, campos magnéticos, sincrotrones de protones, corona solar y medios interplanetarios. Existe un volumen voluminoso de trabajo teórico sobre la teoría cinética de los plasmas. En este trabajo, El equipo de investigación primero describió brevemente tres de las inestabilidades cinéticas más frecuentemente estudiadas habilitadas por el plasma OFI para el estudio cuantitativo en el laboratorio. Por ejemplo, cuando los electrones del plasma se componen de dos o más corrientes (haces) de propagación conjunta o contrapropagación, pueden volverse inestables. Si bien existe una gran cantidad de trabajo teórico sobre inestabilidades cinéticas en plasmas, quedan por verificar en el laboratorio. Los equipos de investigación habían estudiado previamente estas inestabilidades pasando haces de electrones relativistas a través de plasmas o creando dos plasmas interpenetrantes.
En este trabajo, Zhang y col. mostró que un plasma de helio ultrarrápido OFI (ionización inducida por campo óptico) con una distribución de velocidad de electrones anisotrópica dependiente de la polarización (EVD) conocida era susceptible a la transmisión cinética, filamentación e inestabilidades de filamentación tipo Weibel. Midieron las tasas de crecimiento y las frecuencias de estas inestabilidades utilizando la dispersión de Thomson resuelta en el tiempo. Compararon las mediciones con simulaciones por computadora autoconsistentes (exactas) de partículas en la celda (PIC) y con la teoría a partir de entonces, y observó un buen acuerdo.
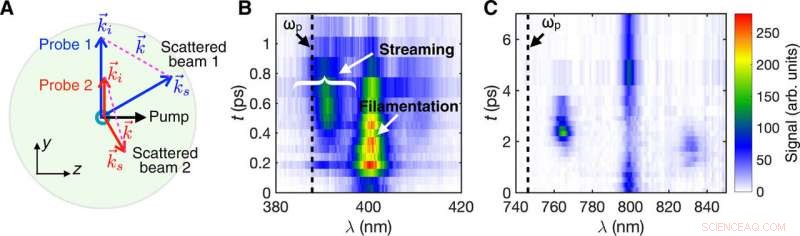
Diagrama de dispersión de Thomson (TS) y ejemplos de espectros TS medidos. (A) diagrama de coincidencia de k donde un plasma de helio producido por un 50-fs, El láser de bomba CP (LP) de 800 nm se diagnostica mediante un láser de 400 nm, sonda 1 (800 nm, sonda 2) láser atravesando el plasma con un retardo variable. Los espectros TS medidos con resolución temporal se muestran en (B) y (C) para las bombas CP y LP, respectivamente. Tenga en cuenta que las escalas de tiempo para las dos polarizaciones son diferentes. Las líneas discontinuas marcan la posición de la frecuencia de plasma esperada correspondiente a la densidad del plasma. El conjunto de datos completo se obtiene escaneando el tiempo en pasos de 50 a 200 fs, y cada paso es el promedio de 20 eventos de dispersión individuales. El tiempo t =0 se define como el tiempo en el que la bomba y la sonda se superponen entre sí (determinado al ubicar la posición del frente de ionización visto en un diagrama de sombras formado por la sonda en la misma ubicación que el haz de la sonda). Crédito:Science Advances, doi:10.1126 / sciadv.aax4545
En los experimentos y simulaciones, El equipo inicializó las funciones anisotrópicas EVD (distribución de velocidad de electrones) ionizando el primer y segundo electrón de helio (He) utilizando pulsos de láser Ti-Sapphire polarizados circularmente (CP) o polarizados linealmente (LP). Monitorearon el potencial de ionización del electrón como la intensidad del láser requerida para ionizar más del 90 por ciento de los átomos de He a través de un mecanismo de túnel desarrollado en otros lugares. Durante los experimentos, la función EVD del segundo electrón He era "más caliente" que la del primer electrón He. Zhang y col. obtuvieron los resultados después del paso de pulsos lineales de una simulación de partículas en celda (PIC) 3-D, que construyeron utilizando el código OSIRIS. La distribución del momento de los electrones se asemejaba a una forma de "doble rosquilla" para los láseres de polarización circular (CP) y una distribución de dos temperaturas en la dirección de los láseres de polarización lineal (LP). Confirmaron que los plasmas producidos de esta manera tienen funciones de EVE. Los valores medidos por el equipo de investigación coincidieron excelentemente con los valores esperados de la simulación PIC.
Luego, el equipo de investigación utilizó simulaciones 2-D de inestabilidades de flujo cinético e inestabilidades de filamentación activadas por ionización de campo óptico (OFI) en un plasma de He. Respectivamente, tanto la inestabilidad del flujo como de la filamentación comenzaron a crecer inmediatamente después de la creación del plasma. Observaron que la inestabilidad de la transmisión eventualmente se saturaba y humedecía muy rápidamente y Zhang et al. por lo tanto, se esperaba de manera similar que la inestabilidad de la filamentación tuviera un comportamiento temporal comparable. En etapas posteriores, La inestabilidad de la filamentación similar a Weibel impulsada por una anisotropía de los electrones a temperatura reducida pero finita comenzó a dominar en el plasma.
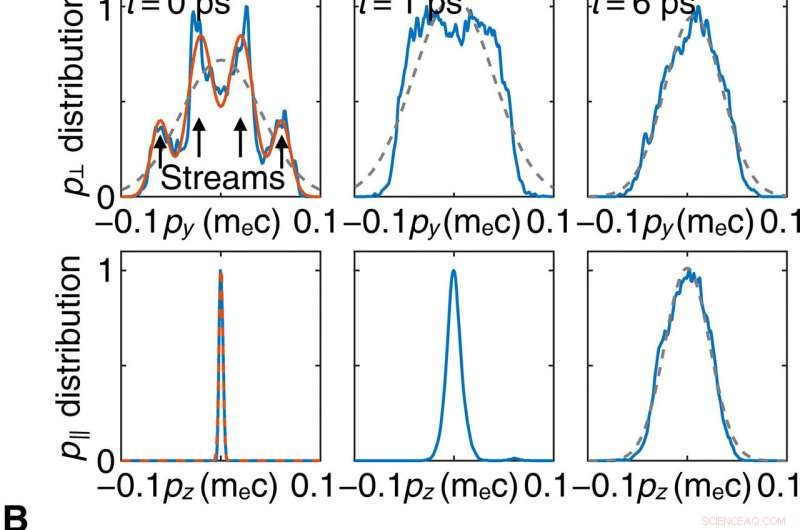
Evolución de la anisotropía térmica del plasma OFI. La fila superior (inferior) en (A) muestra la función de distribución py (pz) de los electrones en t =0, 1, y 6 ps. La línea gris discontinua es un ajuste gaussiano a la distribución. La distribución inicial puede aproximarse mediante cuatro haces maxwellianos a la deriva en el plano transversal, como lo indican la línea roja y las flechas. La línea punteada roja es un ajuste gaussiano a la distribución pz. (B) La línea azul muestra la anisotropía de la misma simulación que en (A), que no incluye colisiones. La línea roja muestra la simulación de la evolución de la anisotropía de un plasma preionizado con solo colisiones de Coulomb incluidas. (C) La energía del campo magnético promedio en función del tiempo muestra dos fases de crecimiento distintas correspondientes a los regímenes de filamentación y Weibel, respectivamente. Crédito:Science Advances, doi:10.1126 / sciadv.aax4545
Para obtener más información sobre la inestabilidad cinética, Zhang y col. sondeó un vector de onda. Para esto, utilizaron un láser de 400 nm o un láser de 800 nm con un ancho de banda de 5 nm y un ancho de pulso de 100 femtosegundos (fs) y probaron los componentes electrostáticos de las inestabilidades del plasma. Midieron los espectros y observaron dos características notables. En primer lugar, la característica del electrón creció y se saturó para amortiguarse en un marco de tiempo mucho más corto que el tiempo para la colisión electrón-electrón. Próximo, el cambio espectral de la característica del electrón mostró un comportamiento anómalo de la onda de Langmuir habitual (oscilaciones de plasma electrostáticas). La frecuencia máxima de la característica electrónica y la existencia de la característica de frecuencia cero fueron evidencia esencial para Zhang et al. para corroborar la transmisión y las inestabilidades filamentosas en la configuración. El equipo de investigación investigó más transmisiones, filamentación e inestabilidades de Weibel inducidas por láseres de polarización circular ampliamente dentro del sistema experimental.
Los científicos también rastrearon la evolución de las distribuciones de velocidad de los electrones y la anisotropía de temperatura de la ionización del campo óptico en una simulación 2-D. Modelaron consistentemente la ionización y la evolución del plasma en la simulación mientras excluían las colisiones de Coulomb para aislar el efecto de las inestabilidades en la anisotropía de la temperatura. Observaron inestabilidades cinéticas en los experimentos, debido a lo cual la anisotropía del plasma disminuyó rápidamente.
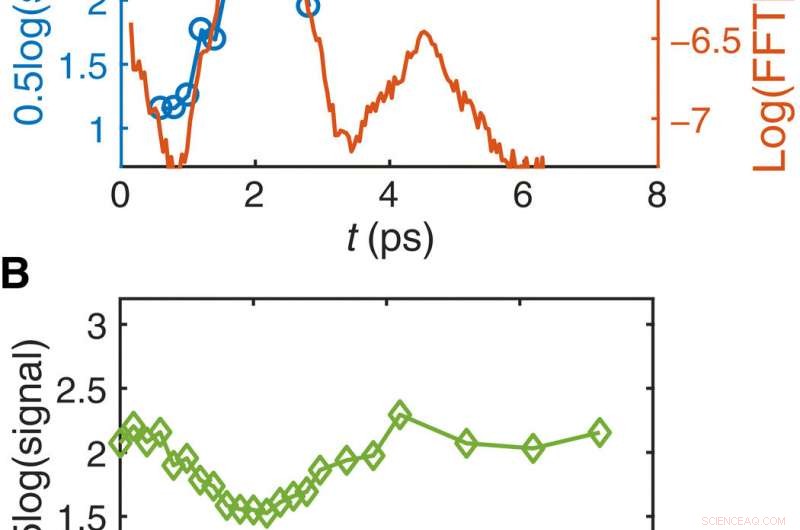
Inestabilidades en un plasma ionizado por un láser LP. (A) Evoluciones medidas (azul) y simuladas (rojo) de la magnitud de las fluctuaciones de la densidad electrónica de la inestabilidad de la transmisión. (B) La magnitud medida del modo de frecuencia cero en función del tiempo, mostrando un comportamiento oscilatorio con un período acústico iónico aproximado. Crédito:Science Advances, doi:10.1126 / sciadv.aax4545
A medida que la inestabilidad de Weibel se saturó en la simulación, los campos magnéticos se autoorganizaron en una estructura cuasi-helicoidal como se predijo en otros lugares. Usando más simulaciones, Zhang y col. confirmaron que las colisiones de electrones no jugaron un papel significativo durante los primeros 10 picosegundos después de la formación del plasma. Durante este tiempo, Las inestabilidades cinéticas dominaron la isotropización del plasma, sin embargo, eventualmente, las colisiones termalizarán el plasma.
El equipo de investigación también investigó las inestabilidades cinéticas inducidas por láseres de polarización lineal, que mostró resultados contrastantes con los láseres polarizados circularmente. En este caso, la inestabilidad fue impulsada por electrones reflejados, que se propaga a través de electrones de movimiento más lento. El espectro de frecuencia del modo era más estrecho que con los láseres CP. El proceso experimental también tardó más en crecer y saturar la inestabilidad de la transmisión. Zhang y col. observó un notable acuerdo entre las mediciones y la simulación.
De este modo, Chaojie Zhang y sus colegas mostraron la posibilidad de generar EVD de "diseñador" utilizando una combinación de condiciones que incluyen diferentes polarizaciones, longitudes de onda, perfiles de intensidad y medios ionizantes. El equipo controló la velocidad de deriva y las temperaturas transversales de las corrientes cambiando la elipticidad de la polarización para suprimir las inestabilidades de la corriente o de la filamentación. Los investigadores demostraron que los plasmas OFI ultrarrápidos no eran térmicos con una anisotropía de gran velocidad. Los plasmas sufrieron inestabilidades filamentosas y fluidas, seguido de inestabilidad de filamentación similar a Weibel para isotropizar el plasma. Cuando midieron la frecuencia dependiente de la polarización y la tasa de crecimiento de estas inestabilidades cinéticas, los resultados concordaron bien con la teoría cinética y las simulaciones. De este modo, el equipo de investigación desarrolló y demostró una plataforma fácilmente desplegable para estudiar las inestabilidades cinéticas del plasma en el laboratorio.
© 2019 Science X Network