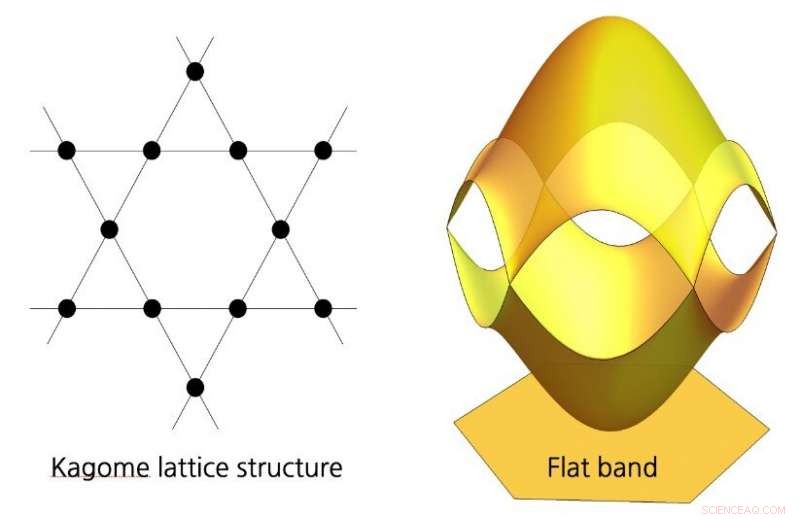
(Izquierda) La estructura de celosía de Kagome en el espacio real. (Derecha) La estructura de bandas correspondiente en el espacio de momento. La banda inferior es la banda plana que exhibe un espectro de nivel de Landau anómalo. Crédito:IBS
La geometría de un objeto indica su forma o la relación de sus partes entre sí. ¿Sabías que los electrones de los sólidos también tienen estructuras geométricas? En mecánica cuántica, un electrón en sólidos toma la forma de una onda con periodicidad de modo que el estado electrónico periódico, el llamado estado de Bloch, se puede caracterizar especificando su energía y momento cristalino que es proporcional a su número de onda. La relación entre la energía y el momento cristalino de los electrones se denomina estructura de bandas de los sólidos. Para electrones en sólidos, la curvatura de Berry y la métrica cuántica de los estados de Bloch toman el papel de la curvatura y la distancia de un objeto en geometría.
De hecho, la geometría de los estados cuánticos es uno de los conceptos centrales que subyacen a diversos fenómenos físicos, que van desde el célebre efecto Aharonov-Bohm hasta las fases topológicas de la materia desarrolladas más recientemente. Por ejemplo, la curvatura local de Berry es responsable del transporte de Hall anómalo, mientras que su integral sobre un colector cerrado bidimensional da el número de Chern, un número entero que describe la conductividad Hall cuantificada. Sin embargo, en comparación con la física de la curvatura Berry, los efectos de la métrica cuántica sobre los fenómenos físicos se comprenden menos, especialmente en sólidos, aunque hay varios trabajos recientes que proponen los observables físicos relacionados con la métrica cuántica. Especialmente, No ha habido una pauta clara para la búsqueda de materiales en los que se puedan observar las propiedades físicas relacionadas con la métrica cuántica.
El profesor Yang Bohm-Jung y el Dr. Rhim Jun-Won en el Centro de sistemas de electrones correlacionados del Instituto de Ciencias Básicas (IBS) de la Universidad Nacional de Seúl, Seúl Corea del Sur, y el Dr. Kim Kyoo del Instituto de Investigación de Energía Atómica de Corea, Daejeon, Corea del Sur, informaron que encontraron una manera de medir la distancia cuántica de los estados de Bloch en sólidos mediante la aplicación de un campo magnético. Más específicamente, los investigadores han examinado el espectro de energía bajo un campo magnético, llamado espectro de nivel de Landau, de bandas planas en las celosías de kagome y tablero de ajedrez, y observó una expansión anómala del nivel de Landau que surge de la banda plana. Asombrosamente, encontraron que la propagación de energía total del nivel de Landau de la banda plana está determinada únicamente por la distancia cuántica máxima entre los estados de Bloch de la banda plana. A saber, La distancia cuántica de los estados de Bloch en un sólido se puede medir aplicando un campo magnético a materiales bidimensionales con bandas planas.
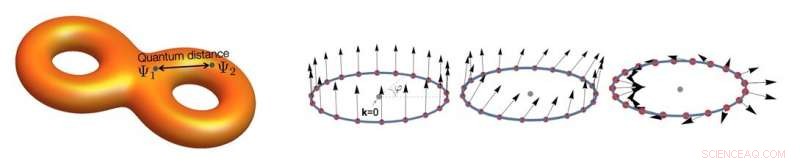
(Izquierda) Una caricatura que representa la estructura geométrica de los estados de Bloch. La distancia cuántica mide la distancia mecánica cuántica entre dos funciones de onda de Bloch. (Derecha) Las funciones de onda de Bloch de la banda plana se pueden representar mediante el pseudo-spin (flechas). El ángulo relativo entre dos pseudo-espines corresponde a la distancia cuántica entre los estados de Bloch relevantes. Crédito:IBS
Recientemente, Los materiales bidimensionales con bandas planas han recibido una gran atención como una nueva plataforma para realizar estados electrónicos intrigantes. Una banda plana indica una estructura de banda electrónica en la que la energía no cambia cuando se varía el impulso del cristal. Estas intrigantes estructuras de bandas planas aparecen en varias celosías bidimensionales, incluida la celosía de kagome, celosía de tablero de ajedrez, etc. El grupo de teoría del equipo de investigación de IBS CCES se dio cuenta de que, en muchos de los sistemas de banda plana, la curvatura de Berry de los estados de Bloch es cero debido a la simetría de la celosía. Si la curvatura de Berry es estrictamente cero, naturalmente se puede esperar que la geometría de los estados de Bloch esté determinada únicamente por la métrica cuántica. Este interesante aspecto motivó al equipo de teoría del IBS a considerar seriamente los materiales bidimensionales con bandas planas como un campo de juego prometedor para estudiar las propiedades físicas relacionadas con la métrica cuántica.
De hecho, la regla de cuantificación semiclásica predice que una banda parabólica ordinaria bajo un campo magnético forma niveles de Landau discretos igualmente espaciados, y la diferencia de energía entre los niveles vecinos de Landau es inversamente proporcional a la masa efectiva de los electrones. Cuando se aplica a una banda plana con una masa efectiva infinita, la teoría semiclásica predice un espaciado de nivel de Landau cero, de modo que una banda plana permanece inerte bajo el campo magnético. En este estudio, los investigadores observaron una naturaleza bastante peculiar del espectro de niveles de Landau que contrasta fuertemente con la norma convencional. Informaron que los niveles de Landau de las bandas planas se extendieron a la región vacía del espacio energético donde no hay estados electrónicos disponibles en ausencia de campo magnético.
Los investigadores encontraron que la clave de un espectro de nivel de Landau tan inusual es el hecho de que la banda plana en las celosías de kagome y tablero de ajedrez se cruza con otra banda parabólica en un punto. La singularidad en la función de onda de la banda plana que surge del punto de cruce de la banda induce un efecto geométrico no trivial relacionado con la distancia cuántica de la función de onda, que a su vez induce un espectro de nivel de Landau anómalo. El primer autor, El Dr. Rhim Jun-Won afirma:"Comprender el papel del cruce de bandas en bandas planas fue la clave para describir los niveles anómalos de Landau. Este hallazgo proporciona una forma práctica de extraer sin ambigüedades la distancia cuántica en sólidos".
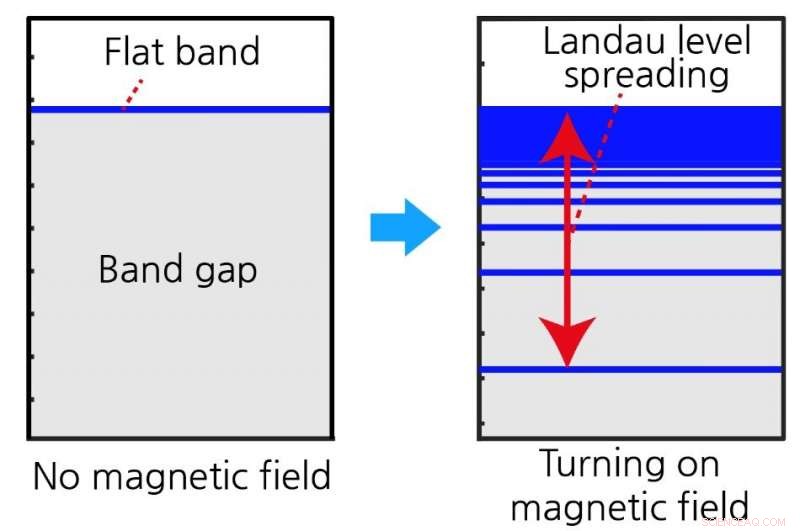
(Izquierda) El espectro de energía de la banda plana cuando el campo magnético está ausente. No hay un estado de energía disponible dentro de la banda prohibida. (Derecha) El espectro de energía bajo el campo magnético (los niveles de Landau) que surge de la banda plana. Los niveles de Landau se distribuyen en la región con huecos y el ancho de la expansión del nivel de Landau está determinado por la distancia cuántica de los estados de Bloch de la banda plana. Crédito:IBS
Este estudio muestra que la distancia cuántica o la métrica cuántica también pueden desempeñar un papel crucial en la determinación de las propiedades de los materiales, como lo hace la curvatura de Berry. Al contrario de los trabajos anteriores, este estudio identificó claramente los sistemas de celosía candidatos en los que se maximiza el efecto de la métrica cuántica mientras que se minimiza el efecto de curvatura de Berry, y descubrió una forma de extraer directamente la distancia cuántica en sólidos por primera vez. Considerando el tremendo impacto del concepto de curvatura Berry en la comprensión de las propiedades de los sólidos, Es natural esperar que este estudio pueda facilitar el estudio futuro sobre las propiedades geométricas de los sólidos relacionadas con la métrica cuántica y la búsqueda de materiales en los que se puedan observar las respuestas físicas relacionadas.
El profesor Yang Bohm-Jung explica que "este resultado proporcionaría un paso crítico hacia la comprensión completa de las propiedades geométricas de los estados cuánticos en los sólidos. Como hay muchas estructuras reticulares bidimensionales que albergan bandas planas, nuestro estudio puede desencadenar futuras actividades de investigación para descubrir nuevos fenómenos geométricos relacionados con la métrica cuántica en varios materiales de materia condensada ".