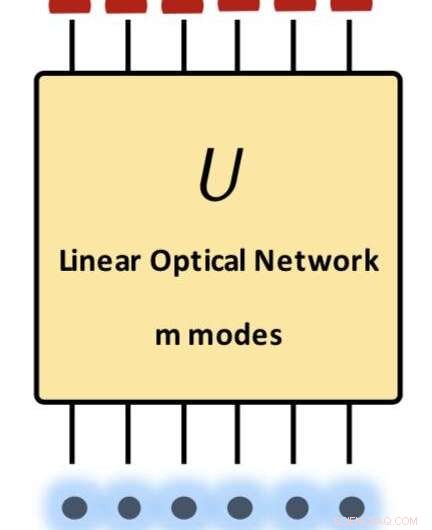
Resumen de nuestro resultado principal:un límite superior de las amplitudes de transición para óptica lineal. Los estados inicial y final son productos de los estados de Fock. La matriz U presenta cualquier transformación unitaria realizable en óptica lineal. Crédito:Science China Press
La óptica lineal constituye uno de los mejores ejemplos para demostrar la física cuántica. Funciona a temperatura ambiente, y se puede observar con dispositivos relativamente simples. La óptica lineal implica procesos físicos que conservan el número total de fotones. En el caso ideal, si hay 100 fotones al principio, no importa lo complicado que sea el proceso físico, Al final quedarán exactamente 100 fotones.
Los fotones son partículas bosónicas que no interactúan. Sin embargo, todavía pueden interferir entre sí, exhibiendo efectos cuánticos no triviales. Un ejemplo típico es el experimento Hong-Ou-Mandel, donde dos fotones idénticos se envían a un dispositivo experimental. Después de una simple transformación lineal, los dos fotones parecen como si estuvieran pegados y no estuvieran dispuestos a separarse. Además de proporcionar una comprensión fundamental de la mecánica cuántica, el estudio de la óptica lineal también ha dado lugar a muchas aplicaciones científicas.
En años recientes, las propiedades únicas de los sistemas ópticos lineales también han inspirado el desarrollo de la teoría de la complejidad computacional. En 2012, El profesor Scott Aaronson del MIT (actualmente en la Universidad de Texas en Austin) propuso un método óptico lineal para demostrar la supremacía cuántica (computacional), que se basa en el concepto de muestreo de bosones. Más específicamente, Aaronson sugirió que para una clase de problemas de muestreo basados en sistemas ópticos lineales, En la práctica, sería imposible aplicar cualquier computadora clásica para simular. Esta idea desencadena inmediatamente una carrera por alcanzar el estado de "supremacía cuántica". Muchos laboratorios de óptica cuántica de todo el mundo se han interesado en desarrollar sistemas de muestreo de bosones para batir récords en términos de números de fotones. Por otra parte, Los informáticos están ocupados aplicando supercomputadoras para elevar el listón para lograr la supremacía cuántica.
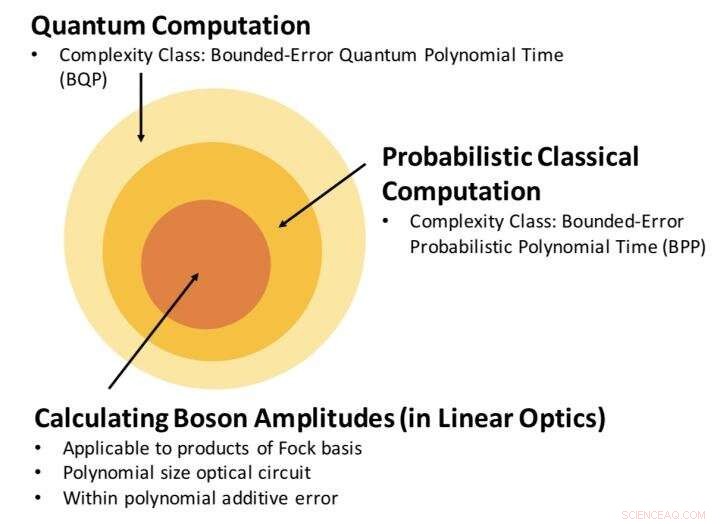
Relación entre la clase de complejidad de estimar la amplitud del bosón, y computación clásica y cuántica. Nuestro resultado establece que al calcular la amplitud del bosón, con un error aditivo polinomial, es un problema dentro de BPP. Crédito:Science China Press
Sin embargo, en términos de problemas prácticos, aplicar el modelo de muestreo de bosones no es un buen enfoque. Por lo tanto, Aaronson planteó una pregunta en 2012:además de los problemas de muestreo, ¿Pueden los investigadores explotar la óptica lineal para lograr la supremacía cuántica en términos de problemas de decisión con una respuesta SÍ / NO? Recientemente, Prof. Man-Hong Yung, El profesor asociado de SUSTech y sus colegas publicaron un artículo titulado "Límite universal en bosones de muestreo en óptica lineal y sus implicaciones computacionales" en Revista Nacional de Ciencias ( NSR ), ofreciendo una solución completa al problema abierto planteado por Aaronson.
Específicamente, El equipo de Yung descubrió un límite fundamental en las probabilidades de transición de los sistemas ópticos lineales, restringir la capacidad de transferir bosones utilizando dispositivos ópticos lineales. Junto con las herramientas de la óptica cuántica, desarrollaron un algoritmo clásico que puede estimar eficientemente la amplitud de transición con un error acotado. Como consecuencia, estos resultados conducen a una respuesta negativa al problema abierto de Aaronson. En otras palabras, para codificar problemas de decisiones difíciles, es necesario hacer uso de sistemas de óptica cuántica más complicados en lugar de solo ópticas lineales.
Como dominio interdisciplinario entre la física cuántica y la informática, La ciencia de la información cuántica sigue siendo un área de investigación muy activa. Por un lado, los resultados del equipo de Yung contribuyen a la base teórica de la óptica cuántica; por otra parte, además del muestreo de bosones, estos resultados apuntan a una nueva perspectiva sobre los problemas de complejidad computacional en términos de óptica cuántica. Indudablemente, en el futuro, deberíamos esperar ver muchos más resultados interesantes como estos en esta área.