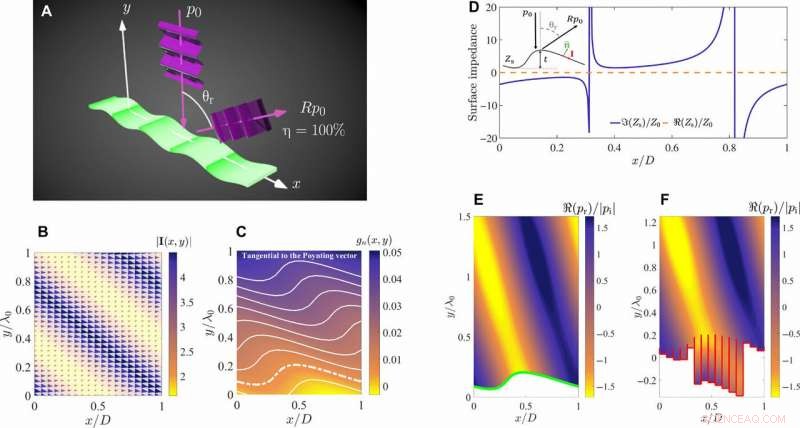
Metaespejo reflectante anómalo. El estudio se realiza para ϕr =0, θi =0 °, y θr =70 °. (A) Representación esquemática del problema. (B) Distribución del vector de intensidad dictada por las ecuaciones derivadas del estudio. (C) La función de nivel de curva normalizada gn (x, y) =g (x, y) / I0. Las líneas blancas representan las curvas de nivel, es decir., las curvas paralelas al vector de intensidad en cada punto. (D) Impedancia de superficie. La curva de nivel correspondiente asociada con esta impedancia está marcada con la línea discontinua en (C). Simulación numérica de la respuesta de una metasuperficie conforme al poder:(E) Metasuperficie modelada como un límite reactivo no homogéneo. La línea verde muestra la superficie límite. (F) Implementación real utilizando tubos con extremos rígidos. Las líneas rojas indican superficies modeladas como límites rígidos. Crédito: Avances de la ciencia , doi:10.1126 / sciadv.aau7288
Las metamateriales son metamateriales bidimensionales (2-D) que pueden controlar las ondas de dispersión de un haz de luz. Sus aplicaciones incluyen polarizadores de hoja delgada, divisores de haz, lentes y tubos de dirección de haz. Estas estructuras pueden controlar y transformar ondas incidentes basadas en la ley de reflexión y refracción generalizada (GSL; ley de Snell generalizada y ley de reflexión generalizada), que establece que pequeños elementos de cambio de fase pueden controlar las direcciones de las ondas reflejadas y transmitidas.
En un estudio reciente, Ana Díaz-Rubio y sus colaboradores en Finlandia y Estados Unidos investigaron metasuperficies reflectantes conocidas como metaespejos. El trabajo se basó en la distribución del flujo de potencia y la adaptación de la forma del reflector para diseñar las distribuciones deseadas de los campos incidente y reflejado. resultando en metaduplicaciones altamente eficientes. El trabajo investigó la reflexión anómala y la división del haz de ondas acústicas y electromagnéticas, y los resultados ahora se publican en Avances de la ciencia .
Solo recientemente los científicos entendieron la física de la transformación de ondas por metasuperficies. Para comprender las dificultades de controlar los reflejos de las metasuperficies, los científicos consideraron el flujo de energía en las proximidades de reflectores anómalos. Por ejemplo, En teoria, Habrá regiones donde el poder transportado por el incidente y las ondas de interés reflejadas "ingresen" a la metasuperficie y regiones donde el poder "emerja" de la superficie. Los fenómenos indicaron que las metasuperficies requerían una respuesta de ganancia / pérdida distribuida periódicamente o un comportamiento fuertemente no local. Para lograr esto en la práctica, Los científicos pueden diseñar cuidadosamente el perfil de resistencia de la superficie de los materiales para lograr reflejos de alta eficiencia en direcciones arbitrarias.
Es más, Se pueden controlar simultáneamente dos ondas reflejadas para diseñar completamente los reflejos de las ondas. Trabajos anteriores habían demostrado que el diseño de metasuperficies de gradiente de fase basado en la ley de reflexión generalizada tenía mayores eficiencias si el ángulo de deflexión no excedía de 40 a 45 grados. Para diseñar dispositivos altamente eficientes como hologramas o lentes, Las ondas reflejadas múltiples deben controlarse sin reflejos parásitos. Como mecanismo de guía de energía, Los científicos han diseñado previamente campos evanescentes cuidadosamente detrás de las metasuperficies para realizar interacciones no locales entre metaátomos.

Divisor de haz asimétrico (70 y 30%). El análisis se realiza para ϕ1 =ϕ2 =0, θi =0 °, y θr =± 70 °. (A) Representación esquemática del problema. (B) Distribución de la intensidad. C) La función de nivel de curva normalizada gn (x, y) =g (x, y) / I0. Las líneas blancas representan las curvas de nivel, es decir., las curvas paralelas al vector de intensidad. (D) Impedancia de superficie. La curva de nivel correspondiente asociada con esta impedancia está marcada con la línea discontinua en (C). Resultados numéricos para la metasuperficie conforme a la potencia:(E) Metasuperficie modelada como un límite de impedancia. La línea verde muestra la posición del límite. (F) Implementación real utilizando tubos con extremos rígidos. Las líneas rojas muestran las paredes del tubo modeladas como límites rígidos. Crédito: Avances de la ciencia , doi:10.1126 / sciadv.aau7288
En el nuevo estudio, Díaz-Rubio et al. estudió la posibilidad de crear metaespejos capaces de reflejar ondas en direcciones arbitrarias, sin dispersión parasitaria y sin necesidad de campos evanescentes cerca de la metasuperficie. Los científicos introdujeron un método de diseño multifísico para crear metaespejos acústicos o electromagnéticos para dar forma a las ondas reflejadas. Describieron un método sistemático para diseñar metaespejos teóricamente perfectos basado en un enfoque que contiene cuatro pasos, incluso:
Los científicos realizaron simulaciones numéricas en el estudio utilizando el análisis de elementos finitos del software COMSOL Multiphysics. Los diseños propuestos se simularon y calcularon utilizando condiciones de contorno de paredes duras. Los científicos simularon la iluminación como una onda plana perfecta, implementado usando condiciones de dominio de campo de presión de fondo.
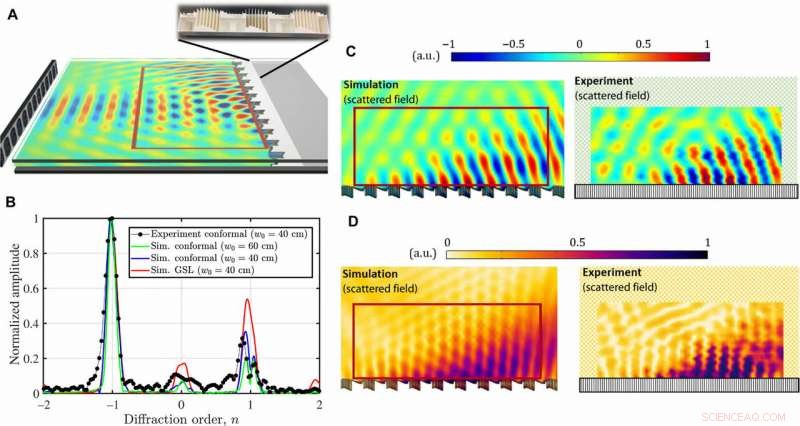
Verificación experimental. (A) Representación esquemática de la configuración experimental y una fotografía de la muestra fabricada. (B) Comparación entre la dispersión normalizada de los metaespejos reflectantes anómalos para diferentes anchos de haz, w0:simulación (sim.) del metaespejo conforme (w0 =40 y 60 cm), verificación experimental del metaespejo conforme (w0 =40 cm), y diseño GSL simulado (w0 =40 cm). La dispersión normalizada se calcula con una transformada de Fourier de los campos de presión a lo largo de una línea sobre las metasuperficies. (C y D) Análisis de la parte real (C) y el cuadrado de magnitud (D) del campo de presión experimental y la comparación con simulaciones numéricas. a.u., unidades arbitrarias. Crédito: Avances de la ciencia , doi:10.1126 / sciadv.aau7288
El enfoque de diseño introducido por Díaz-Rubio et al. no requirió ninguna optimización numérica para la comprensión física de los complejos fenómenos de reflexión y difracción. Por lo tanto, los resultados del estudio proporcionaron una clara ventaja para su uso en el diseño y desarrollo prácticos de dispositivos. Como prueba de concepto, los científicos realizaron una validación experimental en el estudio, para lo cual eligieron metaespejos acústicos capaces de reflejar ondas acústicas normalmente incidentes en la dirección de 70 grados. Díaz-Rubio et al. diseñó los metaespejos utilizando tubos de extremo cerrado impresos en 3D, donde la geometría de la superficie siguió el contorno conforme perpendicular a la dirección del flujo de potencia como se simuló numéricamente.
En el experimento, los científicos realizaron mediciones para obtener los campos dispersos. Los resultados mostraron que viajaba más energía en la dirección deseada, mientras que una cantidad residual de energía se dispersó en otras direcciones. Las imperfecciones observadas fueron consecuencia del ancho finito de la viga; por lo tanto, el rendimiento de los metaespejos fue mejor con vigas más anchas. De este análisis, los científicos demostraron que la energía esparcida en direcciones no deseadas podría reducirse notablemente cuando aumentaron el ancho del haz en la configuración experimental. De este modo, Díaz-Rubio et al. mostró una mayor eficiencia del metaespejo conforme en comparación con el diseño convencional correspondiente.
Para mediciones experimentales de mapeo de campo con ondas acústicas, Los científicos utilizaron una matriz de altavoces con 28 altavoces para enviar un haz modulado en Gauss a la metasuperficie y escanear el campo utilizando un micrófono en movimiento en un paso de 2 cm. Obtuvieron el campo acústico en cada punto, que luego calcularon utilizando el método de la transformada de Fourier. Los campos acústicos medidos a 3000 Hz estaban en excelente acuerdo con las simulaciones. Cuando los científicos midieron la eficiencia de los metaespejos basándose en la energía dispersa, obtuvieron un valor del 96,9 por ciento, validando su enfoque.
La validación experimental reportada en este estudio por Díaz-Rubio et al. es la primera implementación de un metaespejo acústico reflectante anómalo que podría superar los límites de eficiencia de los diseños anteriores basados en GSL. Los científicos habían utilizado previamente metasuperficies conformes para diseñar dispositivos de camuflaje, ilusiones y lentes ópticas y acústicas, donde las metasuperficies se adaptaron a la forma de cuerpos dispersos o reflectantes. Relativamente, en el concepto propuesto por Díaz-Rubio et al. metasuperficies conformes adaptadas a la distribución de potencia deseada de los campos. Como resultado, el concepto se puede utilizar para realizar transformaciones de campo complejas con alta eficiencia como se demostró experimentalmente en el estudio y queda por investigar en la práctica en el futuro.
© 2019 Science X Network