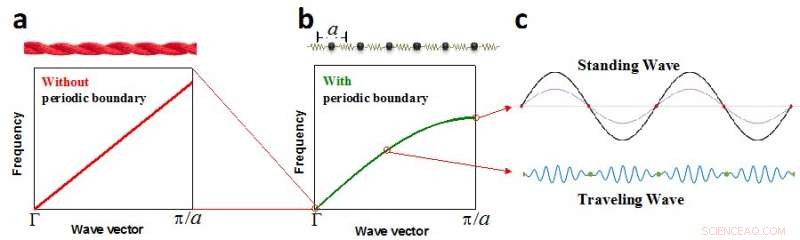
(a) dispersión lineal de fonones basada en el supuesto de ondas acústicas-elásticas, (b) la dispersión del fonón sinusoidal considerando la condición de frontera periódica, (c) onda estacionaria de celosía (arriba) y onda viajera (abajo). Crédito:Science China Press
La conductividad térmica de celosía afecta fuertemente las aplicaciones de materiales relacionados con la funcionalidad térmica, como la gestión térmica, Recubrimientos de barrera térmica y termoeléctricos. Para comprender la conductividad térmica de la celosía de manera más cuantitativa y de una manera rentable y en tiempo, muchos investigadores han dedicado sus esfuerzos y han desarrollado algunos modelos físicos utilizando dispersiones de fonones aproximadas durante el siglo pasado.
La mayoría de estos modelos utilizan una dispersión fonética lineal, propuesto por Debye en 1912 basado en un supuesto de onda acústica-elástica (Fig. 1a), mientras que otros modelos implican ajustar parámetros sobre la dispersión de fonones o carecen de ecuaciones detalladas para las propiedades de transporte de fonones. La dispersión lineal de fonones de Debye ofrece muchas simplificaciones en las propiedades de transporte de fonones, y fue la aproximación más común en el siglo pasado. La dispersión lineal de Debye predice con éxito la dependencia de T3 de la capacidad calorífica a temperaturas muy bajas, y la capacidad calorífica se acerca al límite de Dulong-Petit a altas temperaturas. Sin embargo, la naturaleza de la periodicidad en las disposiciones atómicas conduce a una condición de frontera periódica para las vibraciones de la red en sólidos (Fig. 1b), que en realidad crea ondas estacionarias de celosía en los límites de Brillouin (Fig. 1c). Esto no satisface la suposición de ondas acústicas elásticas de Debye, como lo propusieron Born y von Karman (BvK) en 1912, el mismo año en que Debye propuso la dispersión lineal.
Esto da como resultado una desviación significativa de la dispersión de Debye para materiales cristalinos periódicos cuando los fonones con vectores de onda están cerca de los límites de Brillouin (fonones de alta frecuencia). Cuando estos fonones están involucrados para el transporte de fonones (es decir, a temperaturas no extremadamente bajas), La dispersión de Debye conduce a una sobreestimación de la conductividad térmica de la red debido a la sobreestimación de la velocidad de grupo para estos fonones de alta frecuencia, como se observa en materiales con cientos de conductividad térmica de celosía medida conocida y los detalles necesarios para una predicción de modelo rentable y en el tiempo, según nuestro mejor conocimiento (Fig. 2g yh que muestran una desviación media absoluta de ~ + 40%). Además, La dispersión de Debye también sobreestima el límite inferior teóricamente disponible de la conductividad térmica de la celosía, lo que lleva a que las violaciones de la conductividad térmica de la red medida sean incluso más bajas que el mínimo teórico actual predicho (basado en el modelo Debye-Cahill) como se observa en decenas de materiales.
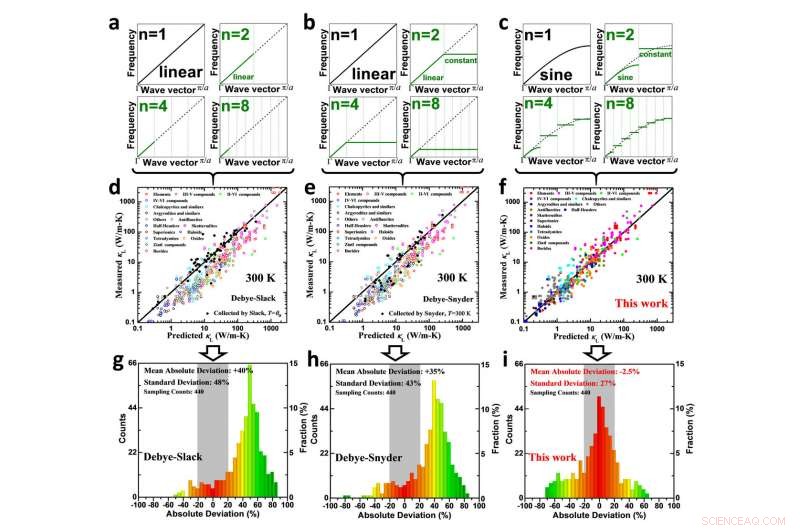
Comparación de la dispersión de fonones (a, byc), conductividad térmica de celosía medida versus predicción (d, eyf) y los análisis de error correspondientes (g, h e i) para el modelo Debye-Slack (a, d y g), Modelo de Debye-Snyder (b, e y h) y el desarrollado en este trabajo considerando la condición de contorno periódico (c, gyi) para sólidos cristalinos. Crédito:Science China Press
Este trabajo tiene en cuenta la condición de frontera BvK, y revela que el producto de las dispersiones acústicas y ópticas produce una función sinusoidal. En el caso de que el contraste de masa (o constante de fuerza) entre átomos sea grande, la dispersión acústica tiende a ser una función sinusoidal. Esta dispersión de tipo seno de hecho existe tanto en los materiales más simples como en los más complejos. Aproximando la dispersión acústica a seno, la condición de límite BvK reduce posteriormente las ramas ópticas restantes para ser una serie de modos localizados con una serie de frecuencias constantes. Si bien los cálculos de los primeros principios permiten una dispersión de fonones más detallada, Un desarrollo de la dispersión de fonones racionalizada para una predicción rentable y en tiempo del transporte de fonones es significativo debido a que los cálculos de primeros principios consumen mucho tiempo y son computacionalmente costosos.
Este trabajo utiliza la racionalización mencionada anteriormente de las dispersiones de fonones, lo que permite incluir tanto las contribuciones a la conductividad térmica reticular de fonones acústicos como ópticos. Esta mejora en las dispersiones de fonones mejora significativamente la precisión de una predicción rentable y rentable sobre la conductividad térmica de celosía de sólidos sin ningún parámetro de ajuste (Fig. 2c, mostrando una desviación media absoluta de solo -2,5%), y por lo tanto ofrece un diseño más preciso de sólidos con la conductividad térmica de celosía esperada. Es más, Este trabajo elimina con éxito la contradicción de que la conductividad térmica de la celosía medida sea incluso más baja que el mínimo teórico predicho en base a una dispersión lineal de Debye (Fig. 3). Esto proporcionaría la posibilidad teórica de racionalizar la conductividad térmica de la celosía para que sea más baja de lo que se piensa actualmente. abriendo más oportunidades para el avance de materiales térmicamente resistivos para aplicaciones, incluyendo termoeléctricos.
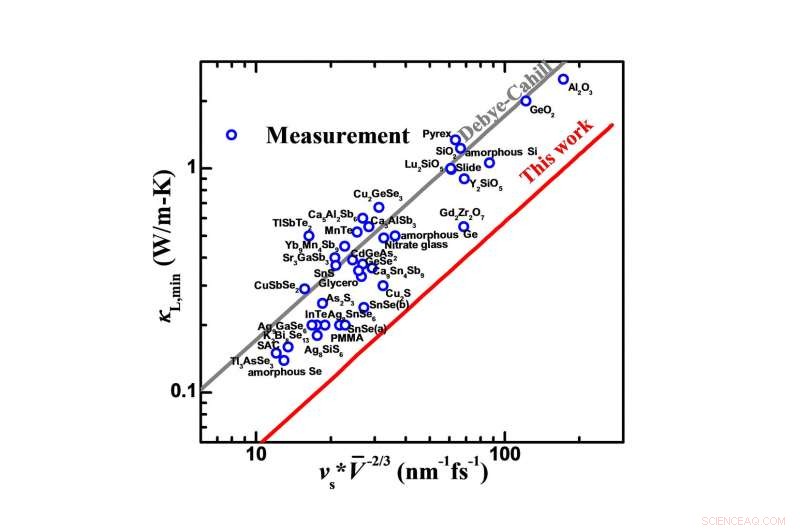
Comparación de la conductividad térmica de celosía mínima medida (? L, min) y predicciones basadas en una dispersión desarrollada según la condición de frontera periódica o en una dispersión lineal de Debye (modelo Debye-Cahill). Crédito:Science China Press