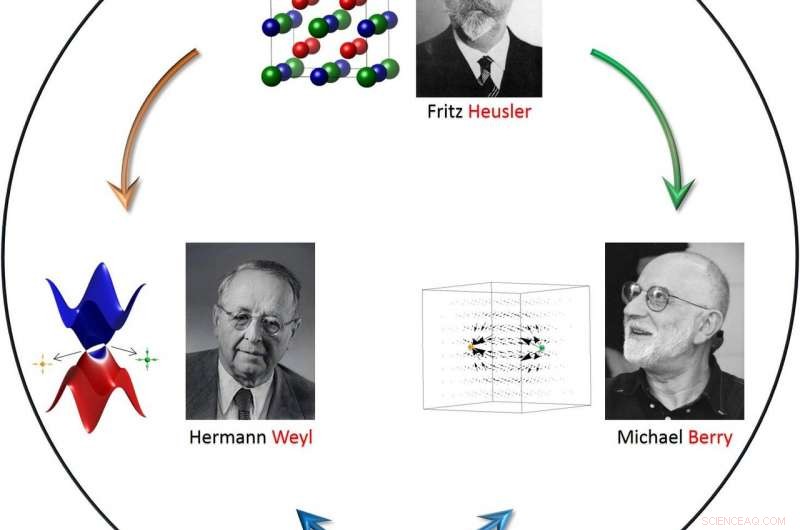
La figura muestra la conexión entre los fermiones de Weyl y la fase Berry y su realización en la familia de compuestos Heusler. En el panel superior, presentamos una disposición atómica típica de una aleación de Heusler completa donde las esferas roja y azul son metales de transición (como el cobalto o el hierro), siendo el rojo más electropositivo que el azul, y la esfera verde es un elemento del grupo principal (como el silicio o el galio). En el panel inferior, Se muestra la estructura electrónica del semimetal Weyl. Los puntos amarillo y verde brillante presentan los monopolos magnéticos en un semimetal de Weyl quiral y las flechas negras indican la curvatura de Berry en el espacio de momento. Crédito:Heusler:Isabellenhütte GmbH &Co. KG; Weyl:ETH Zürich Bildarchiv; Berry:Michael Berry
Los científicos del Instituto Max Planck de Física Química de Sólidos han escrito un artículo de revisión sobre materiales topológicos magnéticos en la familia de compuestos de Heusler. La revisión explica la conexión entre topología, simetría y magnetismo a un nivel adecuado para estudiantes de licenciatura en física, química y ciencia de los materiales con un conocimiento básico de la física de la materia condensada.
Fritz Heusler (1866-1947), Hermann Weyl (1885-1955) y Michael Berry (1941-) son tres científicos de renombre cuyo trabajo ha llevado a nuevos e importantes conocimientos sobre la ciencia de los materiales. topología y física de la materia condensada. Estos tres campos de la ciencia se han unido recientemente con el descubrimiento de nuevas y emocionantes propiedades cuánticas en nuevas clases de material que podrían permitir nuevas ciencias, incluidas las tecnologías informáticas y la catálisis.
Heusler es el nombre del descubridor de compuestos en su mayoría magnéticos que fueron de interés hace bastante tiempo. Pero recientemente se descubrió que estos compuestos albergan propiedades topológicas no triviales que abren un gran campo de física novedosa. Escondidos en la estructura de bandas de energía de estos materiales hay puntos singulares que pueden describirse con herramientas matemáticas que se originan en Weyl; estos puntos están asociados con el descubrimiento de cuasi-partículas que ahora se llaman fermiones de Weyl. No se encuentran entre las partículas elementales de la física de altas energías, pero creemos que existen en materiales sólidos y determinan su topología. El tercer nombre Berry representa los efectos medibles que revelan la física en cuestión. Bajo ciertas condiciones bien definidas existe un campo vectorial, similar al campo magnético, llamada curvatura de Berry. Determina la magnitud de una serie de efectos importantes, como el efecto Hall anómalo y el efecto Hall de giro. Es el arte del experimentalista modificar adecuadamente los materiales para ajustar la curvatura de Berry y así hacer visible la topología. En esta revisión se dan un gran número de ejemplos de varias propiedades de simetría de los compuestos de Heusler, una gran clase de materiales que se pueden ajustar fácilmente para mostrar ferromagnéticos, antiferromagnético, orden magnético no colineal o compensado. Estos ordenamientos magnéticos dan lugar a efectos eléctricos y termoeléctricos pronunciados cuyas huellas dactilares se descubren y explican, incluidas las estructuras de giro de vórtice en forma de partículas, los antiskyrmiones que son típicos de un cierto subconjunto de compuestos de Heusler.
Teniendo en cuenta la gran cantidad de compuestos inorgánicos existentes y la gran cantidad de materiales topológicos no magnéticos recientemente propuestos, Los compuestos de Heusler sirven como un sistema modelo para la comprensión y el impacto del magnetismo en la topología. Romper la simetría de inversión del tiempo a través del magnetismo o un campo magnético externo puede conducir a efectos aún mayores que en los materiales no magnéticos basados en la gran separación entre los puntos de Weyl de diferentes quiralidades. Basándonos en un estudio sistemático de los materiales de Heusler, predecimos que hay una gran cantidad de materiales topológicos magnéticos esperando ser descubiertos.
Con respecto a las aplicaciones, el gran efecto Nernst y los efectos Hall clásicos y cuánticos alrededor de la temperatura ambiente basados en las altas temperaturas de Curie de los compuestos de Heusler y sus parientes tienen el potencial de tener un gran impacto en la conversión de energía y los dispositivos electrónicos cuánticos para la espintrónica o la computación cuántica.