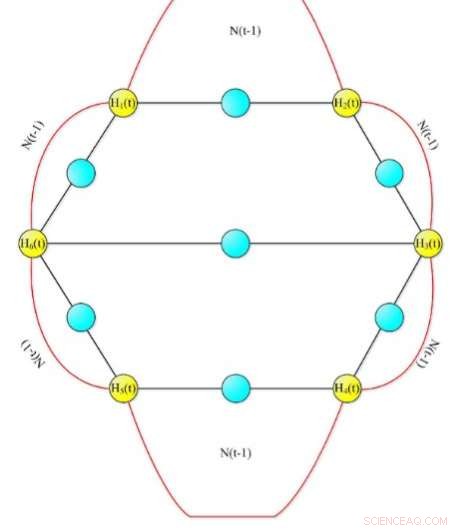
Diagrama del modelo de red aleatorio. Crédito:Springer
Las redes a menudo se describen como árboles con ramas que se extienden. La forma en que se ramifica el árbol depende de la lógica detrás de la expansión de la red, como expansión aleatoria. Sin embargo, algunos aspectos de estas redes que se expanden aleatoriamente son invariables; en otras palabras, presentan las mismas características, independientemente de la escala de la red. Como resultado, toda la red tiene la misma forma que una o más de sus partes.
En un nuevo estudio publicado en EPJ B , Fei Ma de la Universidad Normal del Noroeste en Lanzhou, Provincia de Gansu, Porcelana, Los colegas de anc calculan el número total de árboles de expansión en redes que se expanden aleatoriamente. Este método se puede aplicar al modelado de modelos de red sin escala, cuales, como resulta, se caracterizan por propiedades de mundo pequeño. Esto significa, por ejemplo, que los miembros de la red solo exhiben seis grados de separación, como la mayoría de la gente de nuestra sociedad.
Previamente, varios modelos de red se basaron en gráficos que consistían en una agregación de vértices con bordes de conexión. Pero no fueron suficientes para modelar redes de la vida real, como redes de usuarios de redes sociales. En lugar de, redes complejas, donde la red se crea aleatoriamente, se han convertido en los pilares de la informática y las matemáticas discretas modernas. Usando datos de redes de la vida real, y aprovechando la experiencia obtenida de las redes artificiales creadas para dar cuenta de funciones específicas, los autores diseñan modelos más realistas que son más complejos que sus predecesores.
En este estudio, los autores se centran en desarrollar un método recursivo para calcular el número de árboles de expansión en una red, lo cual es particularmente útil para predecir su capacidad para tolerar fallas que ocurren al azar. Ser capaz de encontrar el número de árboles de expansión en modelos de red tiene implicaciones para varios campos científicos, como las matemáticas aplicadas, informática teórica, física y Química.