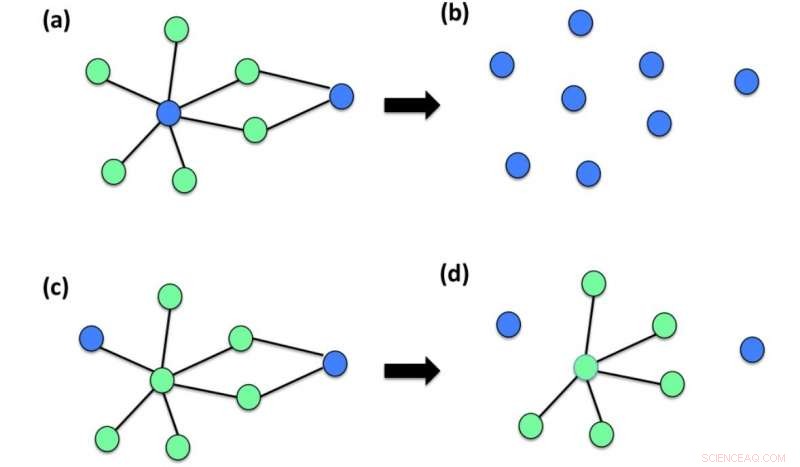
Aquí se muestra que diferentes realizaciones del daño inicial son más o menos dañinas para una red. El panel (a) muestra un daño inicial de una red conectada que afecta exclusivamente a dos de los N =8 nodos de la red (el nodo azul sindica los nodos dañados los nodos verdes indican los nodos no dañados). El panel (b) muestra que este daño inicial es muy perjudicial para la red y da como resultado un componente gigante de tamaño R =1. El panel (c) muestra otra configuración de daño inicial de la misma red que afecta solo a dos nodos de la red. En este caso, el panel (d) muestra que el efecto del daño se reduce y la mayor parte de la red permanece conectada dando como resultado un componente gigante R =6. Crédito:Ginestra Bianconi
Un marco teórico que explica el riesgo de eventos raros que causan grandes interrupciones en redes complejas, como un apagón en una red eléctrica, ha sido propuesto por un matemático de la Universidad Queen Mary de Londres.
Los eventos raros pueden desmantelar abruptamente una red con consecuencias mucho más graves de lo habitual y comprender su probabilidad es esencial para reducir las posibilidades de que sucedan.
Una red está formada por un conjunto de nodos y los enlaces entre ellos. Por ejemplo, las redes eléctricas son redes cuyos nodos son centrales eléctricas conectadas por la red eléctrica. De manera similar, una red ecológica, a los que se podría aplicar el marco, está formado por especies conectadas por interacciones ecológicas como una relación depredador-presa.
Por lo general, si algunos de los ganglios están dañados, redes como estas son lo suficientemente robustas como para seguir siendo funcionales, pero en raras ocasiones los daños específicos pueden conducir al desmantelamiento de toda la red y causar grandes apagones o cambios de régimen ecológico. como un colapso ecológico.
Los matemáticos a menudo usan la teoría de la filtración, una rama bien desarrollada de las matemáticas aplicadas que estudia la respuesta de una red al daño de una fracción aleatoria de sus nodos, para arrojar luz sobre estos fenómenos. Sin embargo, esta teoría solo es capaz de caracterizar la respuesta promedio de una red al daño aleatorio. Por lo tanto, la predicción del comportamiento promedio no se puede utilizar para estimar el riesgo de colapso de la red como resultado de un evento poco común.
Este estudio establece una teoría de percolación de gran desviación que caracteriza la respuesta de una red a eventos raros. El marco teórico propuesto captura correctamente el efecto de configuraciones de daños raros que se pueden observar en redes reales. Curiosamente, el trabajo revela que las transiciones discontinuas de percolación (colapsos abruptos de una red) están ocurriendo tan pronto como se toman en consideración eventos raros.
El marco teórico podría permitir el desarrollo de estrategias para sostener las redes identificando qué nodos deben conservarse para evitar un colapso.
Ginestra Bianconi, autor del estudio, dijo:"Existe una necesidad urgente de evaluar el riesgo de colapso en respuesta a configuraciones raras de daño inicial. Este resultado arroja luz sobre la fragilidad oculta de las redes y su riesgo de colapso repentino y podría ser especialmente útil para comprender los mecanismos para evitar el catastrófico desmantelamiento de redes reales ".
Añadió:"Es importante estimar el riesgo de una cascada dramática de fallas porque se quiere reducir el riesgo. En el diseño de una red eléctrica que debe proporcionar la energía a todo un país se quiere evitar eventos raros en los que tienes grandes apagones, o en el diseño de estrategias de preservación de un ecosistema actualmente diversificado y próspero, desea saber cuál es la probabilidad de un colapso ecológico repentino y una extinción masiva. Por lo tanto, es necesario comprender este riesgo de que ocurran estos eventos ".
El presente estudio de gran desviación de la percolación considera exclusivamente la percolación de nodos en redes individuales como las mencionadas. Sin embargo, Ginestra Bianconi sugiere que la metodología descrita podría extenderse al estudio de modelos más detallados de propagación de fallas de eventos.